• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Початкових параметрів

Визначення кутових та лінійних переміщень методом

Рівняння пружної лінії зігнутої балки

В інженерній практиці розраховують балки не тільки на міцність, але й на жорсткість. При згині жорсткість характеризується здатністю балки чинити опір викривленню. При деформації в межах пружності зігнуту вісь балки називають пружною лінією. Відхилення будь-якої точки осі балки від первісної прямої називають прогином. Кут повороту будь-якого перерізу балки відносно його початкового положення називають кутом повороту перерізу.

Раніше було установлено, що кривизна пружної лінії прямо пропорційна згинальному моменту (8.17)

.

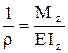З курсу вищої математики відомо, що

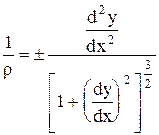, (8.34)

таким чином

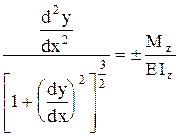. (8.35)

Рівняння (8.35) називають диференціальним рівнянням пружної лінії і інтегрування цього рівняння пов’язане з великими труднощами. Тому в тих випадках, коли прогини невеликі, величиною 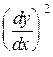порівняно з одиницею можна знехтувати. Тоді дістанемо наближене диференціальне рівняння пружної лінії у вигляді

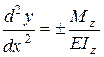. (8.36)

Знак кривизни може не збігатися зі знаком згинального моменту і залежить від напрямку координатних осей. Якщо вісь у направити вверх а вісь х вправо, то знаки у² і М_z збігаються, тому в (8.36) запишемо знак “плюс”

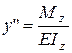. (8.37)

Інтегруючи це рівняння один раз, дістанемо рівняння кутів повороту

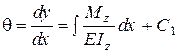. (8.38)

Інтегруючи вдруге, знайдемо

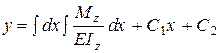, (8.39)

де С₁ і С₂ -сталі інтегрування, які можна знайти із граничних умов.

Наприклад, для балки, показаної на рисунку 8.13 граничні умови

Рисунок 8.13

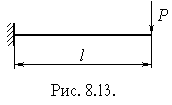
такі: при х=0, y(0)=0 i q(0)=0 (8.40)   Враховуючи, що для цієї балки

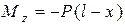
після інтегрування (8.38) і (8.39) будемо мати

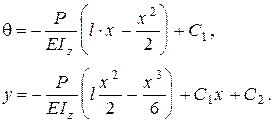(8.41)

Використовуючи граничні умови (8.40), маємо С₁=С₂=0. Знайдені значення С₁ і С₂ підставимо в рівняння (8.41) тоді одержимо рівняння кутів повороту

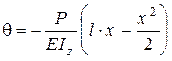
і рівняння пружної лінії

.

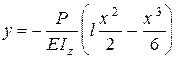Підставивши х=l, знайдемо кут повороту і прогин вільного кінця балки

.

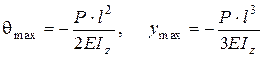Знак “мінус” говорить про те, що переріз повернувся вправо і балка прогнулась вниз.

Визначення переміщень методом безпосереднього інтегрування диференційного рівняння пружної лінії в випадку балок з великою кількістю ділянок ускладнено. Ці труднощі пов'язані не з інтегруванням диференціальних рівнянь, а з технікою визначення довільних сталих інтегрування - складанні і розв'язуванні систем лінійних алгебраїчних рівнянь. Так, якщо балка має n ділянок, то інтегрування диференціального рівняння (8.36) необхідно виконувати для кожної ділянки. В такому випадку буде 2n сталих інтегрування, які визначають із умов на границях ділянок. Тому на практиці часто використовують метод початкових параметрів, який базується на диференціальних залежностях, справедливих для будь-якого перерізу балки між кутом повороту q та моментом M_z і дозволяє при будь-якій кількості ділянок звести розв'язання до визначення всього двох сталих - прогину і кута повороту перерізу в початку координат.

Рисунок 8.14

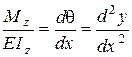, (8.42)   між прогином y та кутом повороту q 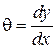  . (8.43)   При використанні цього методу початок координат розміщують в крайньому лівому перерізі і він є загальним для всіх ділянок балки.

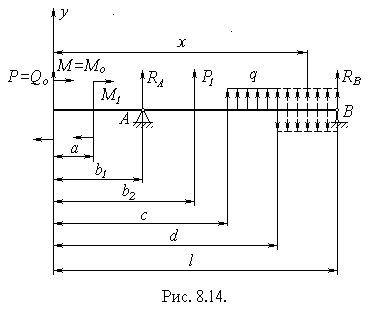
Згинальний момент визначають як алгебраїчну суму моментів всіх сил розміщених зліва від перерізу. При цьому зовнішній зосереджений момент M₁ (рисунок 8.14), прикладений на відстані a від початку координат, множать на величину (x-a)⁰ , яка дорівнює 1, а розподілене навантаження, у випадку його обриву (наприклад при x=d) продовжують до перерізу, в якому визначають переміщення і починаючи з перерізу x=d вводять розподілене навантаження протилежного напрямку. Інтегрування диференціального рівняння виконують не розкриваючи дужок.

Напишемо вираз для згинального моменту в перерізі з координатою “x” (рисунок 8.14)

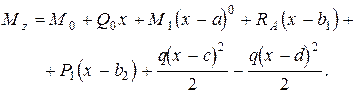(8.44)

Проінтегруємо (8.37) з врахуванням (8.44) один раз, одержимо рівняння кутів повороту для балки сталої жорсткості

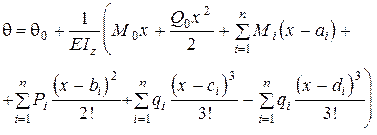(8.45)

Інтегруючи вдруге, одержимо рівняння прогинів

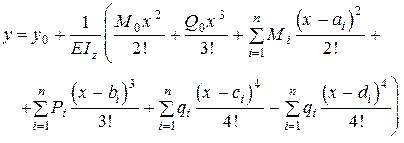(8.46)

В перерізі балки, де взято початок координат, в загальному випадку будуть діяти поперечна сила, згинальний момент, а також будуть мати місце кут повороту і прогин, які ми позначили відповідно Q₀ , M₀ , q₀ , y₀ і називатимемо їх далі початковими параметрами (рисунок 8.14). Для балки, показаної на рисунку 8.14, Q₀=P, M₀=M, а значення q₀ і y₀ можна визначити із умов закріплення

y(b₁)=0, y(l)=0.

Слід відмітити, що при визначенні кута повороту і прогину в перерізі з координатою x в рівняння (8.45) і (8.46) входять тільки ті навантаження, які знаходяться між початком координат і перерізом.

Приклад. Напишемо рівняння кутів повороту і прогинів для балки, показаної на рисунку 8.15.

Рисунок 8.15

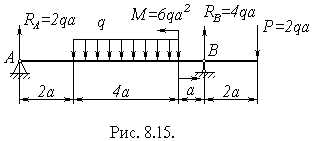
Рівняння прогинів: y0=0, оскільки початок координат збігається з опорою,   M0=0, Q0=RA=2qa.

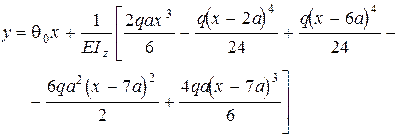
Початковий параметр q₀ визначимо із умови: при х=7а , y(7а)=0

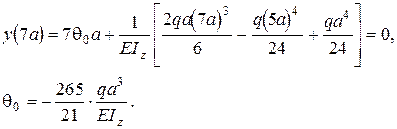
Тепер рівняння прогинів приймає вигляд

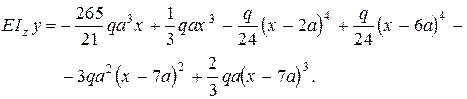
Запишемо рівняння кутів повороту

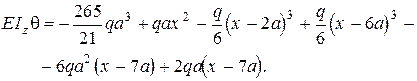
Визначимо, використовуючи ці рівняння, вертикальне переміщення і кут повороту перерізу B, для якого x=2a

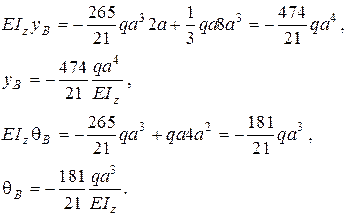
Знак “мінус” говорить про те, що при х=2а (переріз В) балка прогинається вниз, а переріз повертається вправо.

ДОДАТОК А

Механічні характеристики вуглецевих конструкційних сталей

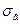
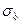
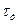
Марка сталі				Відносне вдовження d, %, при l=10d	Ударна в'язкість ак ´10-5 (Нм)/м2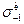
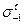
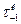
не менше			МПа
МПа
20Г 30Г 50Г 20Х 40Х 45Х 30ХМ 35ХМ 40ХН 50ХН 40ХФА 38ХМЮА 12ХН3А 20ХН3А 30ХН3А 40ХНМА 30ХГСА			- - - - - - - - - - - - 390 - - - 400 - - - -		- - - -	16-22 17-22 19-25 20-27 22-30 23-32 25-34 27-35 - 31-38 - 22-32 29-36 35-38 40-50 31-41 47-51 38-49 42-55 39-47 42-45 52-70 50-70 51-54	12-15 12-46 - 17-21 17-22 18-24 19-25 20-26 - 22-28 - - - - -	8-12 10-13

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. Визначення оптимальних параметрів системи.
3. Визначення основних параметрів газгольдера
4. Визначення основних параметрів грошових потоків.
5. Визначення основних параметрів складів
6. Визначення параметрів і показників для вимірювання кожного процесу та націлення їх на величини
7. Визначення параметрів, що підлягають оцінюванню.
8. Визначення та контроль метереологічних параметрів
9. Вимірювання параметрів
10. Вимірювання параметрів вібрацій
11. Вимірювання параметрів електротехнічних пристроїв.
12. Вимірювання параметрів лінійного руху

Переглядів: 1215