• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Основи теорії подібності.

Незважаючи на високий рівень розвитку сучасної гідродинамічної теорії, далеко не всі практичні задачі можуть бути вирішені теоретично з достатньою точністю і надійністю.

При створенні сучасних гідравлічних машин та пристроїв, літаючих апаратів, гідрологічних споруджень тощо, гідродинамічний розрахунок є важливим і обов’язковим етапом проектування, але все ж заключна оцінка властивостей і характеристик машин, які проектуються або споруджень проводиться на підставі експериментальних досліджень моделей або натурного об’єкту.

При постановці гідродинамічного експерименту одним із основних питань є питання про те, по яким правилах повинна бути виготовлена модель об’єкту, який підлягає дослідженням, і по яким залежностям необхідно перерахувати дані досліджень, щоб одержати вірогідний опис натурного гідродинамічного явища. На це питання дає відповідь розділ гідромеханіки, який називається теорією подібності. Теорія подібності по суті, є основою теорії експерименту.

У теорії подібності розрізняють геометричну подібність яка є подібністю границь областей течії, кінематичну подібність під якою мають на увазі подібність полів місцевої швидкості і динамічну подібність сил.

Наведемо більш повне визначення цих видів подібностей.

Нехай ми маємо натурний об’єкт – потік рідини (рис. 1(1)), який має бути гідродинамічно дослідженим, та його модель (рис. 1(2).

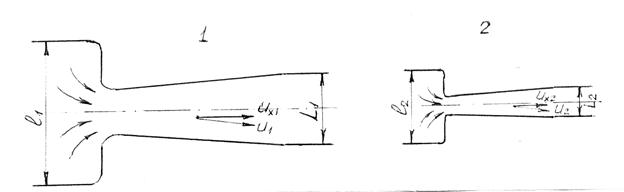
Рис. 1. Потік рідини, який досліджується (1) та його модель (2)

Всі параметри натурного об’єкту (потоку) визначимо індексом 1, а модельного – індексом 2. Щоб одержати зону течії геометрично подібну натурі, розділимо усі лінійні розміри натури на деяке число m_i, яке будемо називати лінійним масштабом, і одержані результати приймемо за відповідні лінійні розміри моделі. Число m_i обирають із практичних міркувань, які диктуються, наприклад, виробничими можливостями лабораторії.

Таким чином, одержуємо зв’язок між геометричними параметрами l₁ і l₂ об’єктів 1 і 2.

.

Лінійні розміри, пов’язані відношенням , називають відповідними або подібними.

Модель 2, геометричні параметри якої задовольняють записаній умові, назвемо геометричною подібністю об’єкту 1.

Інакше можна сказати, що два гідродинамічних об’єкта будуть геометрично подібними, якщо будь-який лінійний розмір одного може бути одержаний із лінійного розміру другого шляхом множення на постійний множник.

Припустимо тепер, що об’єкти 1 і 2 геометрично подібні. Визначимо через U₁ і U₂ швидкості у схожих точках цих потоків, а через Uі₁ і Uі₂ їх однойменні проекції на деяку вісь координат. Якщо відношення:

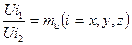
однаково для будь-якої пари подібних точок, то потоки 1 і 2 будуть кінематично подібними.

Кінематичну подібність можна визначити інакше.

Якщо і 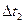- малі інтервали часу, за які рідкі частини проходять подібні відрізки шляху, то

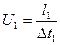і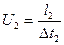

Звідси масштаб часу .

Кінематично подібними називають потоки, в яких відрізки часу, які витрачаються рідкими частинами для проходження подібних відрізків шляху, знаходиться в постійному відношенні.

Розглянемо далі будь-яку пару подібних точок і визначимо величини проекцій на координатні вісі рівнодіючих сил через Fi₁ і Fi₂. Якщо Fi₁/Fi₂=m_F (i=x, y, z) є величина постійна для будь-якої пари подібних точок, то потоки 1 і 2 називають динамічно подібними.

З приведених визначень ясно, що кінематична і динамічна подібність може існувати тільки при наявності геометричної подібності.

Якщо для будь-якої групи гідродинамічних явищ має місто кінематична і динамічна подібність, то її називають групою механічно подібних явищ або групою повної гідродинамічної подібності. Існування на практиці повної гідродинамічної подібності майже неможливо, тому мають справу з частковою подібністю (неповною), при якій виконується пропорційність лише основних (головних) сил.

Для напірних течій у закритих руслах, тобто для потоків у трубах, у гідромашинах тощо, такими силами, як показує аналіз, є сили тиску, в’язкості і сили інерції. На рідину діє також сила тяжіння, але в напірних потоках її дія проявляється через тиск. І. Ньютон запропонував розглядати динамічну подібність, виходячи із умов, що сили, які діють у подібних точках динамічно подібних систем (потоків), у подібні моменти часу мають однакове відношення.

Сили інерції визначаються добутком маси на прискорення, тобто Р=m^.a.

Масу можна виразити як:

m=rV=rL³,

де V – об’єм рідини, м³,

L – лінійний розмір потоку, м.

Прискорення є:

а=L/t²

де t – відрізок часу, с.

Тоді сила інерції:

.

Таким чином, сила інерції пропорційна густині рідини, швидкості у другій степені і площі:

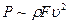
Для потоків, які гідродинамічно подібні 1 і 2, маємо:

Записані умови – це математичний вираз загального закону динамічної подібності, сформульований І. Ньютоном у 1686р.

Приймемо сили інерції за основу і будемо інші сили, які діють на рідину, порівнювати з інерційними. Тоді можемо записати:

(1)

Це відношення, яке є однаковим для подібних потоків, називають числом Ньютона і позначають Ne. Тут під Р мають на увазі основні сили: силу тиску, в’язкості, тяжіння тощо.

Отже, останнє співвідношення (1) являє собою загальний вид закону гідродинамічної подібності.

2. Основні гідродинамічні подібності.

Розглянемо три характерні випадки впливу на рідину, яка рухається, основних сил і знайдемо умови подібності потоків.

1. На рідину діють лише сили тиску і інерції. Тоді р~DpF~DpL² і відношення сил буде:

,

або:

= = Eu (2)

де Еu – безрозмірний критерій, який являє собою міру відношення сил тиску до сил інерції і який називається числом Ейлера.

Із попереднього стає зрозумілим фізичне значення числа Ейлера: це є величина, яка пропорційна відношенню сил тиску до сил інерції.

Таким чином, у тих випадках, коли основними силами, які діють на рідину є сили тиску (у гідравлічних пресах, гідравлічних приводах об’ємної дії, при дослідженнях явищ кавітації тощо) динамічна подібність буде досягнута при виконанні геометричної і кінематичної подібності, а також при рівності чисел Ейлера, які розраховані для схожих точок потоку, який вивчається.

2. Найчастіше у гідродинаміці реальної рідини силою, яка визначає характер руху, є сила внутрішнього тертя між частками рідини, яка обумовлена її в’язкістю. Сили тертя є основними при напірному русі в’язкої рідини по трубопроводам, при русі тіл у повітрі тощо.

Сила внутрішнього тертя рідини може бути визначена згідно з законом І. Ньютона:

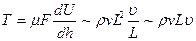
Розділимо останній вираз на та одержимо:

,

або:

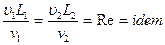, (3)

де Re – безрозмірний критерій, який називають числом Рейнольдса.

Число Re являє собою відношення сил інерції до сил тертя. Таким чином, коли домінуючими силами є сили інерції і тертя, динамічна подібність буде виконана при геометричній і кінематичній подібності, а також якщо Re, яке обчислене для схожих точок, буде однаковим.

3. Розглянемо випадок, коли вирішальне значення мають сили тяжіння (це має місце, наприклад, при плаванні судів, у безнапірних потоках гідротехнічних споруджень, при витіканні рідини через отвір тощо). У цьому випадку в основне рівняння динамічної подібності (число Ньютона) належить ввести сили тяжіння, які можна представити у вигляді:

і тоді:

,

або:

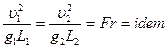
де Fr – безрозмірний критерій, який називають числом Фруда і яке являє собою міру відношення сил інерції до сил тяжіння.

Таким чином, коли домінуючими силами, які діють на рідину, являються сили інерції і тяжіння, то динамічна подібність буде виконана, якщо існує геометрична і кінематична подібність, а також рівність чисел Фруда для схожих точок систем.

Окрім перелічених основних критеріїв подібності (Eu, Ne, Re, Fr), в гідравліці використовують і інші критерії для особливих випадків течії рідини. Так при розгляданні течій, пов’язаних з поверхневим натягом (наприклад, при розпаді струменя краплі, розпилення палива у двигунах), вводять критерій Вебера (We), який дорівнює відношенню сил поверхневого натягу до сил інерції:

,

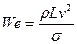де σ – коефіцієнт поверхневого натягу рідини.

А також, критеріальні числа Галілея Ga, який характеризує відношення сил тяжіння до сил інерції:

,

та Архімеда Ar, який характеризує взаємодію архімедової сили, що виникає при різниці густини рідини та сил в’язкого тертя:

.

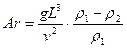3. Режими течії рідини.

Багаточисленні спостереження показують, що у природі існує два різних режиму руху рідини – ламінарний (від латинського lamina – шар, пластинка), при якому частки рідини у потоці рухаються упорядковано у вигляді струмків або шарів, які між собою не змішуються і турбулентний (від латинського turbulentus – вихровий), при якому частки рідини рухаються по складним траєкторіям, які весь час змінюються, внаслідок чого відбувається інтенсивне перемішування частинок рідини.

Вже давно було відомо, що в’язкі рідини (мастила) рухаються здебільшого упорядковано, а малов’язкі рідини (вода, повітря) – майже завжди невпорядковано. Ці спостереження дозволили зробити висновок, що ламінарний режим спостерігається при русі в’язких рідин, а також при русі води через капілярні трубки. Рух води у водопровідних трубах, у різного роду напірних трубопроводах, у каналах, річках тощо при швидкостях течії, які звичайно зустрічаються на практиці майже завжди характеризується турбулентним режимом.

Вивчення ламінарного і турбулентного режимів руху має окремий інтерес через те, що втрати питомої енергії істотно залежать від того, в якому режимі відбувається рух рідини: в ламінарному режимі енергія витрачається тільки на поздовжнє переміщення часток рідини вздовж потоку; в турбулентному режимі витрачається додаткова енергія на поперечне переміщення часток рідини, це пов’язано з неупорядкованим характером руху.

Це положення вперше було висловлено у 1880 році великим російським вченим Д.І. Мендєлєєвим у роботі “Про опір рідин і про повітроплавання”, де було вказано на існування видів рідини, які відрізняються різними залежностями дії сил тертя від швидкості руху.

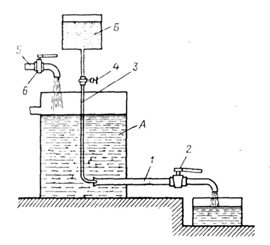
Рис. 2 Схема дослідної установки О. Рейнольдса.

Ясність у питанні про те, як саме буде відбуватися рух рідини у тих чи інших умовах, була внесена у 1883 році дослідним шляхом англійським фізиком Осборном Рейнольдсом.

Установка О. Рейнольдса для дослідження режимів руху рідини представлена на рис. 2. Посудина А заповнюється випробуваної рідиною. До посудини А в нижній її частині приєднана скляна трубка 1 з краном 2, яким регулюється швидкість течії в трубці 1. Над посудиною А розташований бак Б з розчином фарби. Від баку Б відходить трубка 3 з краном 4. Кінець трубки 3 заведений в скляну трубку 1. Поповнення судини А рідиною здійснюється за допомогою трубки 5 з запірним пристроєм 6.

Вимірювання видатку рідини здійснюється завдяки мірному посуду. Відкриваючи частково кран 2 на скляній трубі 1, можна заставити текти рідину із різними швидкостями.

При малих швидкостях руху рідини у трубі підфарбований струмок не розмивається водою, яка його оточує і має вигляд натягнутої нитки. Потік у цьому випадку називається ламінарним.

При збільшенні швидкості руху рідини підфарбовані струмки одержують спочатку хвильовий обрис, а потім майже раптово зникають та розмиваються по всьому перетину труби, фарбуючи всю рідину.

Рух рідини стає неупорядкованим, окремі частки зштовхуються друг із другом та з стінками тощо. Такий рух називається турбулентним.

Цей дослід можна виконати і в зворотному напрямку: починати нагляди з більших швидкостей і постійно зменшувати їх.

Проте, процес переходу одного режиму руху в другий не є зворотним: ламінарний режим переходить у турбулентний при значно більших швидкостях, ніж ті, при яких турбулентний режим переходить у ламінарний.

На основі аналізу результатів експериментальних досліджень та аналізу розмірностей О. Рейнольдс встановив, що критерієм режиму течії рідини є безрозмірна величина, яка являє собою відношення середньої швидкості потоку V і діаметра труби d до кінематичної в’язкості рідини n :

і яку називають критеріальним числом Рейнольдса. По фізичній суті число Re являє собою відношення двох робіт, які діють у рухомій рідині: роботи сил інерції і роботи сил внутрішнього тертя.

Малі значення чисел Re відповідають перевазі роботи сил внутрішнього тертя, а великі значення – перевазі роботи сил інерції.

У результаті експериментів встановлено, що один режим переходить в інший при цілком певній середній швидкості руху потоку. Швидкість, при якій відбувається перехід із одного режиму в іншій, називається критичною. Розрізняють дві критичні швидкості: верхню V_кр.в. і нижню V_кр.н.. При V_кр.в. ламінарний режим переходить у турбулентний, а при V_кр.н. відбувається зворотний перехід. Таким чином межа між ламінарним і турбулентним режимом руху рідини визначаються критичним числом Re_кр.

Сучасними дослідженнями встановлено, що значення Re_кр можуть коливатися у доволі широких межах в залежності від багатьох факторів: умов входу в трубу, шорсткості стінок труби, роду і температури рідини та інших умов.

У розрахунках часто приймають Re_кр (по дослідженням німецького гідравліка Шиллера) для круглих труб в межах приблизно 2320, але ця величина не є універсальною. Так, якщо для руху у прямих трубах Re=2320, то для руху у змійовиках Re_кр=f(d/D), де d – діаметр труби, D – діаметр витка змійовика.

Наприклад, при d/D =0,001 Re_кр=2,2 ^.10³, а при d/D =0,02 Re_кр@5 ^.10³. Необхідно підкреслити, що, наприклад, для процесу осадження Re_кр=0,2, для переміщування Re_кр=50 тощо.

Досліди на пристрої Рейнольдса дозволяють встановити зв’язок між втратами енергії і швидкостями руху рідини у трубі, тобто експериментальним шляхом одержати залежність: h_тр=f(V).

Лекція № 6 «Ламінарний режим руху рідини у трубах»

1. Загальні відомості про визначення втрат напору в трубопроводі.

2. Закон розподілу швидкостей по перетину круглої труби при ламінарному режиму течії рідини.

3. Видаток і середня швидкість ламінарного потоку.

4. Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.

5. Початкова ділянка ламінарної течії.

Читайте також:

1. A) правові і процесуальні основи судово-медичної експертизи
2. R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
3. А .Маршалл - основоположник неокласичної теорії.
4. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
5. Активне управління інвестиційним портфелем - теоретичні основи.
6. Альтернативні теорії вартості
7. Альтернативні теорії капіталу
8. Альтернативні теорії макроекономічного регулювання
9. Альтернативні теорії максимізації
10. Альтернативні уявлення щодо макроекономічного регулювання: теорії раціональних сподівань та економіка пропозиції. Крива Лафера.
11. Анатомо-фізіологічні основи статевого розвитку.
12. Базові поняття теорії і методики фізичного виховання.

Переглядів: 2684