• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівняння Д. Бернуллі для потоку реальної (в’язкої) рідини.

У практиці інженерної діяльності доводиться мати діло не з ідеальною рідиною, а з реальною, якій властиві певна в’язкість, стислість і ряд інших властивостей.

В’язкість реальної рідини викликає опір руху, внаслідок чого має місто втрата частини енергії, яка міститься у рухомому елементарному струмку.

Як тільки що було доведено, величина повної енергії для елементарного струмка ідеальної рідини постійна. У в’язкій рідині енергія вздовж струмка зменшується, переходячи внаслідок тертя у теплову енергію.

Нехай в якомусь із перетинів елементарного струмка реальної рідини питома енергія буде дорівнювати , а у перетині, відлеглому на деякій відстані від нього, . Причому, так як має місто втрата енергії, то >, або: .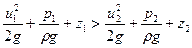

Втрату питомої енергії по довжині струмка між перетинами позначимо через та її можна визначити як різницю питомих енергій у двох перетинах: .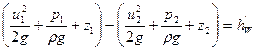

Звідси .

Це є рівняння Д. Бернуллі для елементарного струмка реальної рідини.

Значення складових ми всі розібрали, за виключенням додаткового члена . Так як розмірність питомої енергії є лінійною величиною, то, очевидно, і різниця їх теж буде лінійною величиною, тобто має розмірність висоти стовпа рідини.

Далі, якщо розглядати струмок в’язкої рідини, то повний напір її буде зменшуватися по довжині, тобто: .

А тому, рівні рідини у трубках Піто будуть знижуватись. Лінія, яка з’єднує рівні рідини у трубках Піто, називається напірною, але вона є похилою, яка спадає.

Цей висновок дозволяє пояснити геометричне значення рівняння Д. Бернуллі для елементарного струмка в’язкої рідини: видаток енергії або втрата напіру являє собою різницю між висотою рівня рідини в трубках Піто у початковому перетині і висотою рівня рідини у трубці Піто перетину відносно площини порівняння.

При виведенні рівняння Д. Бернуллі для потоку в’язкої рідини необхідно пам’ятати, що потік складається із сукупності елементарних струмків, а швидкості по перетину потоку реальної рідини не однакові.

Рис. 9

Розглянемо сталий потік реальної (в’язкої) рідини.

Вилучимо в ньому елементарний струмок і для двох його перетинів напишемо рівняння Д. Бернуллі.

Ваговий елементарний видаток струмку можна виразити rgdQ, а тому повна енергія струмків у двох довільно вибраних перетинах може бути визначена наступним виразом:

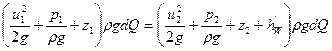
Перепишемо рівняння у такому вигляді:

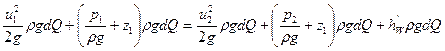
Таким чином, рівняння Д. Бернуллі для цілого потоку в’язкої рідини може бути одержане шляхом складання повних енергій усіх елементарних струмків, з яких складається потік, і втрат енергії.

Необхідно обчислити три інтеграли:

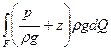1. ; 2. ; 3. .

Так як видаток визначається добутком швидкості на площу живого перетину, то можна перший інтеграл записати як:.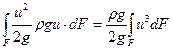

Під знаком інтегралу стоїть значення місцевої швидкості, яка в межах живого перетину потоку являється перемінною.

Із-за нерівномірного розподілення швидкостей доводиться вводити в розглядання середню по перетину швидкість v.

Після заміни під знаком інтегралу перемінної u на постійну v можемо проінтегрувати вираз: .

Одержаний вираз являє собою деяку умовну величину кінетичної енергії потоку. Ця величина відрізняється від “дійсної” величини кінетичної енергії .

В загальному випадку: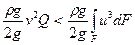

Відношення 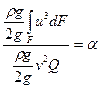і називається коефіцієнтом нерівномірності розподілення швидкостей по живому перетину потоку. Цей коефіцієнт іноді називають коефіцієнтом Коріоліса.

Коефіцієнт a визначають експериментальним шляхом на підставі спеціальних вимірювань швидкостей у різних точках потоку рідини, яка досліджується.

Розглянемо тепер другий інтеграл .

Для обчислення інтегралу 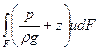необхідно пригадати умови, для яких одержане рівняння Д. Бернуллі – рух сталий і на струмок діє тільки сила тяжіння.

Для цих випадків тиск по перетину розподіляється по закону гідростатики, тобто .

Тому:

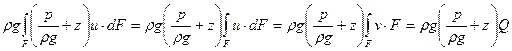
Постійність питомої потенційної енергії справедлива для будь-якої точки живого перетину потоку, який плавно змінюється.

Звернемося тепер до третього інтегралу: .

По аналогії з поняттям про середню швидкість потоку скористаємося поняттям про середню втрату енергії в струмках між двома перетинами.

Позначимо середню втрату енергії через h_W. Тоді:

Тепер рівняння для цілого потоку в’язкої рідини, записане в загальному вигляді можемо переписати:

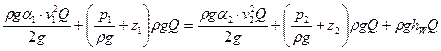
Віднесемо усі елементи потоку до одиниці ваги рідини, тобто поділимо рівняння на rgQ:

Одержане рівняння Д. Бернуллі для цілого потоку в’язкої рідини по своїй будові аналогічно рівнянню для елементарного струмка і записано у формі напорів. Якщо для струмка ідеальної рідини рівняння являє собою закон збереження енергії, то для потоку реальної рідини воно являється рівнянням балансу енергії з урахуванням втрат.

Для більшості практичних розрахунків можна приймати a=1.

Помноживши рівняння Д. Бернуллі на rg, одержимо форму запису рівняння, у якій кожний член його має розмірність тиску:

.

Величину rgz називають гравітаційним тиском; - динамічним тиском.

На практиці для виконання інженерних розрахунків користуються або рівнянням, записаним у формі напорів, або у формі тиску.

Рівняння Д. Бернуллі, являється основним рівнянням гідравліки, за допомогою якого виводяться розрахункові формули для різноманітних випадків руху рідини і вирішуються практичні задачі. При цьому слід мати на увазі, що воно справедливе тільки для сталих потоків або які плавно змінюються з плоскими живими перетинами. Тому використовувати його можна тільки там, де є усі ознаки такого руху.

Звичайно для розв’язання задач на схемі потоку проводять два перетина і горизонтальну площину – площину порівняння. Площину порівняння, щоб було менш невідомих, проводять через центри тяжіння одного або, якщо це можливо, двох перетинів, і тоді z₁ або z₂ або вони обидва будуть дорівнювати нулю. Перетин проводять нормально напряму руху рідини, а місця їх проведення вибирають так, щоб перетини були плоскими, утримували невідомі величини, які підлягають визначенню, і достатнє число відомих величин. Звичайно такими місцями є: вільні поверхні рідини, вхід або вихід із трубопроводу, місця установки вимірювальних пристроїв тощо. Далі, для вибраних перетинів, які нумерують по напрямку руху рідини, записують рівняння Д. Бернуллі, підставляють в нього числові значення відомих величин і розраховують невідомі величини.

При рішенні деяких задач приходиться використовувати рівняння нерозривності і обирати більш двох перетинів; щоб уникнути помилок у розрахунках, тиск в рівняння підставляють абсолютний, а не надмірний (так як в одному із перетинів може бути вакуум).

Лекція № 5 «Основи гідродинамічної подібності. Режими руху рідини»

1. Основи теорії подібності.

2. Основні гідродинамічні подібності.

3. Режими течії рідини.

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Видаток і середня швидкість ламінарного потоку.
7. Вихідного грошового потоку
8. Властивості пуассонівського потоку
9. Втрати напору у трубах при турбулентному режимі руху рідини.
10. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
11. Географічна оцінка туристського потоку
12. Гідродинаміка в’язкої рідини. Сила Стокcа

Переглядів: 3246