• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ідеальної рідини.

Рівняння Д. Бернуллі для елементарного струмка

Розглянемо сталий рух рідини. Відомо, що мірою руху рідини є енергія (кінетична і потенційна), за рахунок якої виконується робота. Виходить, що для одержання рівняння енергії необхідно визначити роботу, яку можуть виконати сили при переміщенні маси на елементарний відрізок довжини по лінії току.

Помножимо кожне із рівнянь системи (8) відповідно на dx, dy, dz. Таким чином визначимо роботу одиничних сил при переміщенні маси рідини. Після помноження одержану систему рівнянь складемо:

.

Розглянемо перш за все ліву частину виразу: dx, dy, dz можна виразити як добуток проекції швидкості на елементарний відрізок часу, тобто

; ; .

Звідки:

; ; .

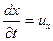Тоді ліва частина рівняння прийме вигляд:

Розглянемо суму трьох складових у скобках. Так як при сталому русі тиск є функцією координат у просторі і не залежить від часу, то вираз являє собою повний диференціал тиску:

Остаточно рівняння енергії прийме вигляд:

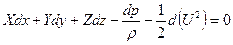(9)

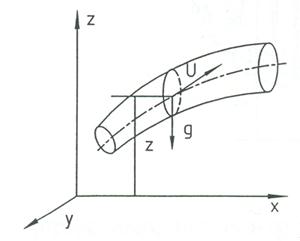
Рис. 5 Схема до виводу рівняння Д. Бернуллі.

Пристосуємо одержану залежність до елементарного струмка ідеальної рідини, яка знаходиться у сталому русі. Для цього виберемо систему координат, в якій вісь Z направлена наверх. В цих умовах проекції одиничних масових сил будуть: Х=0; Y=0; Z=-g. Підставляючи їх значення в рівняння (9) і враховуючи, що у всіх точках живого перетину елементарного струмка частки рідини рухаються з однаковою швидкістю u, одержимо:

,

або: .

Після інтегрування рівняння маємо:

,

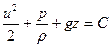або: . (10)

Це рівняння показує, що сума трьох його членів є величиною постійною вздовж елементарного струмка.

Для двох різних положень рухомої частки рідини можемо записати:

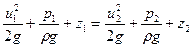(11)

Рівняння (11) являє собою математичний вираз закону збереження енергії вздовж елементарного струмка і називається рівнянням Д. Бернуллі. Воно являється найважливішим рівнянням гідродинаміки, за допомогою якого вирішується багато задач гідродинаміки.

Як виходить із самого доказу рівняння, воно являє собою рівняння енергії. Кожний його член характеризує енергію рідини, яка віднесена до одиниці ваги.

Енергія рідини, яка віднесена до одиниці ваги, називається питомою енергією. Окремі члени рівняння характеризують наступну величину:

z – питому потенційну енергію положення;

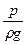- питому потенційну енергію тиску;

- питому кінетичну енергію.

Геометричне та фізичне (енергетичне) розуміння

рівняння Д. Бернуллі.

Для з’ясування значення кожного члена в рівнянні (11) розглянемо елементарний струмок рухомої рідини.

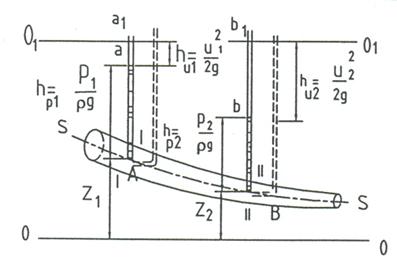
Рис. 6 Геометричне та фізичне (енергетичне) розуміння

рівняння Д. Бернуллі.

Припустимо, що центри тяжіння живих перетинів І-І і ІІ-ІІ струмка розташовані на геометричних висотах z₁ і z₂ від площини порівняння 0-0. У центрах тяжіння перерізів встановлені п’єзометричні трубки. Внаслідок наявності в точках встановлення п’єзометрів тиску рідина в кожному з них встановиться на висотах та 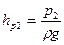. Ці висоти, так як і в гідростатиці, можуть бути названі п’єзометричними. Таким чином, члени рівняння Д. Бернуллі z₁ та z₂ являють собою геометричні висоти центрів тяжіння живих перетинів елементарного струмка над площиною порівняння, а та 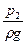- п’єзометричні висоти, які відповідають тискам у центрах тяжіння. Ці два члени рівняння мають розмірність довжини (метри стовпа рідини).

Звернемося тепер до третього члену рівняння, який також має розмірність довжини. Для встановлення третього додатка розглянемо вимірювальний пристрій, який носить назву трубки Піто. Це зогнута під кутом 90^о трубка з наконечником меншого діаметру, ніж діаметр самої трубки. Така трубка, будучи заглиблена у рухому рідину отвором наконечника проти течії рідини, може служити для вимірювання швидкості течії у тій точці, де розташований її наконечник.

Будемо розглядати потік рідини у напірній трубі з встановленою в точці А трубкою Піто (рис. 7). Допустивши, що точка А розташована в перерізі А-А, візьмемо у безпосередній близькості другий перетин В-В. У цьому перетині розмістимо звичайну п’єзометричну трубку таким чином, щоб її нижній кінець находився на верхній межі струмка, ось якого збігається з віссю трубки Піто.

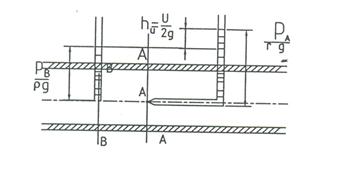
Рис. 7 Схема установки трубки Піто.

Внаслідок дії тиску рідина в п’єзометричній трубці піднімається на п’єзометричну висоту , а в трубці Піто під дією повного напору – на висоту .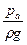

Напишемо рівняння Д. Бернуллі для перетинів А-А та В-В цього струмка відносно площини порівняння, яка збігається із віссю трубки Піто. Для випадку, який розглядається, 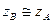, а швидкість руху рідини у точці А дорівнює 0 (так як частка рідини у наконечнику трубки Піто нерухома), тоді у відповідності з рівнянням Д. Бернуллі для двох перетинів маємо:

,

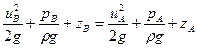так як: , а ,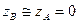

то: ,

де р_А та р_В – гідродинамічний тиск відповідно в перетинах А-А та В-В.

Із останнього рівняння одержимо:

,

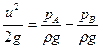де 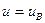- швидкість рідини у межі елементарного струмка.

Різниця висот, що визначена за допомогою двох трубок (п’єзометра та трубки Піто), як звичайно сполучених в одному пристрої, та дорівнює:

,

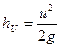називається в гідравліці висотою швидкісного напору.

Виміривши висоту швидкісного напору, можна визначити швидкість руху рідини у тій точці, де вставлений наконечник трубки Піто, по залежності:

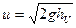
При використанні останньої залежності у практичних випадках вводиться поправочний коефіцієнт, який визначається експериментальним шляхом і враховує втрати енергії.

Повернемося тепер до рис. 6 і розглянемо елементарний струмок ідеальної рідини. Припустимо, що на осі струмку взяті дві точки А та В, висоти яких над площиною порівняння дорівнюють z₁ та z₂. Відкладемо від точок А та В відрізки Аа і Вв, які дорівнюють п’єзометричним висотам в цих точках.

Від точок а та в відкладемо відрізки аа₁ та вв₁, які рівні висотам швидкісного напору та .

Так як сума трьох членів ідеальної рідини постійна вздовж вісі струмка, то вершини вертикальних відрізків аа₁ та вв₁ розташуються на однакових вертикальних відділах від площини порівняння. Таким чином, вершини цих відрізків повинні лежати в одній горизонтальній площині, яку називають напірною площиною 0 – 0.

Далі, якщо ми плавною кривою з’єднаємо рівні рідини у п’єзометричних трубках, то одержимо так звану п’єзометричну лінію.

В гідродинаміці сума трьох висот , , 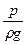z називається повним напором і визначається Н.

Усе викладене і складає в собі геометричне розуміння рівняння Д. Бернуллі.

Особливий інтерес являє з’ясування фізичного значення (або енергетичного) рівняння Д. Бернуллі.

Розглянемо частку рідини, що має масу dm і котра рухається по лінії току s-s. Визначимо повну енергію, якою володіє частка у перетині І-І та ІІ-ІІ. Повна енергія являє собою суму кінетичної і потенційної енергії. Кінетична енергія частки у перетині І-І дорівнює , а у перетині ІІ-ІІ - .

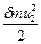Потенційна енергія частки відносно площини порівняння 0 – 0 дорівнює добутку ваги частки на висоту підйому її по відношенню до цієї площини. У перетині І-І частка буде піднята на висоту рівну 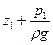(тут - висота, яка відповідає тиску в цьому перетину і який піднімає цю частку). У перетині ІІ-ІІ частка буде піднята на висоту .

Таким чином, частка рідини у перетині І-І володіє потенційною енергією . Аналогічно визначається потенційна енергія у перетині ІІ-ІІ: .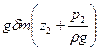

Позначимо повну енергію частки рідини в перетині І-І через , а у перетині ІІ-ІІ - і визначимо її для вказаних перетинів:

.

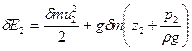Одержані вирази поділимо на вагу частики 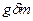, та визначимо повну енергію, яка міститься в одиниці ваги рідини. Енергія, яка міститься в одиниці ваги рідини, називається питомою енергією. Визначимо питому енергію частки у перетині І-І через , а у перетині ІІ-ІІ – через, тоді:

.

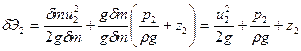Тут додатки і 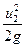- питома кінетична енергія;

і 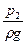- питома потенційна енергія тиску;

z₁ і z₂ – питома потенційна енергія положення.

Згідно з рівнянням Д. Бернуллі (11) сума трьох вказаних членів є постійною:

Тому ми можемо написати, що , тобто сума трьох членів рівняння Д. Бернуллі є сумою питомих енергій: питомої кінетичної енергії, питомої потенційної енергії тиску і питомої потенційної енергії положення.

Рис. 8

Із вищеназваних міркувань виходить, що механічна енергія рухомої рідини може мати три форми: енергію положення, енергію тиску і кінетичну енергію. Перша і третя форми механічної енергії відомі з механіки і вони у рівній мірі відносяться до твердого тіла та рідкого. Енергію тиску досить легко перетворити в механічну роботу. Пристроєм, за допомогою якого здійснюється таке перетворення, є циліндр з поршнем. Покажемо, що при цьому перетворенні кожна одиниця маси рідини виконує роботу кількісно рівну .

Нехай площа поршня F та його хід L, надлишковий тиск рідини р, тиск по другу сторону дорівнює О. Тоді сумарна сила тиску рідини на поршень: Р=рF, а робота - pFL.

Маса рідини, яку необхідно підвести до циліндру для виконання цієї роботи, дорівнює масі у об’ємі циліндру, тобто m=FLr.

Питома робота буде .

Читайте також:

1. Втрати напору у трубах при турбулентному режимі руху рідини.
2. Гідродинаміка в’язкої рідини. Сила Стокcа
3. Гідростатика нестисливої рідини. Закон Паскаля. Гідростатичний тиск. Закон Архімеда
4. Диференціальне рівняння Ейлера для потоку рідини.
5. Диференційні рівняння руху ідеальної рідини.
6. Закон розподілу швидкостей по перетину круглої труби при ламінарному режиму течії рідини.
7. Режими руху рідини.
8. Рівняння видатку рідини.
9. Рівняння Д. Бернуллі для потоку реальної (в’язкої) рідини.
10. Рідини. Явища в рідинах
11. Рух ідеальної рідини. Рівняння нерозривності. Рівняння Бернуллі

Переглядів: 1456