• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рух ідеальної рідини. Рівняння нерозривності. Рівняння Бернуллі

Щоб описати рух частинок рідини або газу можна для кожної точки простору задати вектор швидкості як функцію часу. Сукупність векторів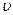, заданих для всіх точок простору, утворює поле вектора швидкості. Якщо провести лінії, дотичні до яких співпадають з напрямком вектора швидкості в кожній точці, то ми отримаємо лінії течії. Поверхню, утворену лініями течії, що проведені через усі точки малого замкнутого контура, називають трубкою течії.

Розрізняють ломінарну або шарувату течію та турбулентну. Ломінарною називають течію, в якій окремі шари при своєму русі не перемішуються (Рис.1.21а). в турбулентній течії відбувається перемішування окремих шарів, утворення завихрень в результаті виникнення нормальної (поперечної) складової швидкості (Рис.1.21б).

В реальних рідинах між окремими шарами рідини виникають сили в’язкого (внутрішнього) тертя. В окремих випадках вплив внутрішнього тертя невеликий і ним можна знехтувати. Абсолютно нестисливу і нев’язку рідину називають – ідеальною.

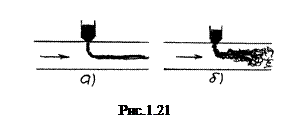
Розглянемо трубку течії, настільки тонку, що в кожному її перерізі швидкість можна вважати однаковою у всіх точках перерізу (Рис.1.22). Можна показати, що

або (1.97)

Рівняння (1.97) називають рівнянням нерозривності, з якого слідує, що чим більша площа перерізу трубки течії, тим менша швидкість течії і навпаки.

Коли рідина рухається по трубі змінного перерізу і різної висоти(Рис. 1.23), то для деякого її об’єму змінюється як кінетична так і потенціальна енергії об’єму рідини. Ця зміна обумовлена дією деяких зовнішніх сил, робота яких рівна зміні потенціальної і кінетичної енергії рідини

.

Після підстановок і перетворень в лівій та правій частинах останнього співвідношення отримаємо вираз

(1.98)

або для довільного перерізу

(1.99)

де 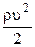– динамічний тиск, – гідростатичний тиск, р – статичний тиск.

Рівняння (1.99) вивів Бернуллі і воно носить його ім’я. Це рівняння виражає закон збереження енергії при стаціонарній течії ідеальної рідини. Для горизонтальної трубки течії і рівняння Бернуллі приймає вигляд

(1.100)

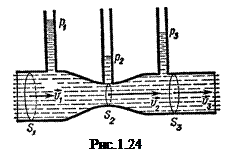Звідси випливає, що в тих місцях труби, де більша швидкість течії, тиск буде меншим і навпаки (Рис.1.24). Якщо рідину налити в посудину площею перерізу , в бічній поверхні якої є отвір площею , то швидкість витікання рідини через отвір визначається за формулою Торічеллі

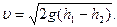(1.101)

Струмінь води, що витікає з бічного отвору посудини створює реактивну тягу, і якщо посудину поставити на візок, то останній почне рухатись разом з посудиною під дією цієї сили

(1.102)

Читайте також:

1. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
2. Асимптотичний підхід до порівняння оцінок
3. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
4. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
5. Вивід основного рівняння фільтрації
6. Втрати напору у трубах при турбулентному режимі руху рідини.
7. Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань
8. Гідродинаміка в’язкої рідини. Сила Стокcа
9. Гідростатика нестисливої рідини. Закон Паскаля. Гідростатичний тиск. Закон Архімеда
10. Головне рівняння відцентрового насоса. Теоретичний напір.
11. Граничні теореми у схемі Бернуллі
12. Два означення інтегралу. Теореми про загальний вигляд інтегралу та залежність двох інтегралів одного диференціального рівняння.

Переглядів: 3862