
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Площину загального положення перетворити на проецюючу.
Пряму загального положення перетворити на проецюючу.
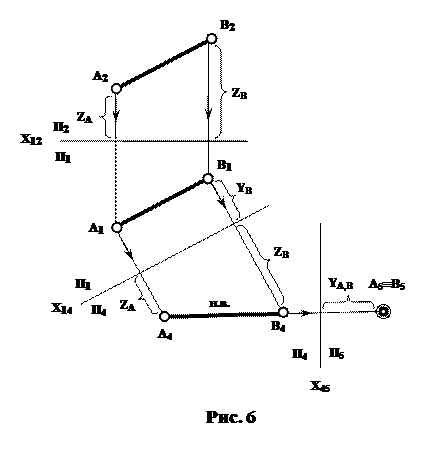 На рис. 6 наведено приклад перетворення прямої АВ на проецюючу, завдяки подвійній за-міні площин проекцій П1 та П2 на додаткові П4 та П5.
На рис. 6 наведено приклад перетворення прямої АВ на проецюючу, завдяки подвійній за-міні площин проекцій П1 та П2 на додаткові П4 та П5.
Спочатку пряма в системі П1П4перетво-рюється на пряму рів-ня, а потім у системі П4П5 – на проецюючу. Тому, вісь Х14 проводимо паралельно А1В1, а вісь Х45 – перпендикулярно А4В4. При цьому АВ спроецюється на П5 у точку А5ºВ5. Це означає, що пряма АВ у новій системі площин проекцій П4П5 перпендикулярна до площини П5.
На рис. 7 зображені проекції площини загального положення, яка задана трикутником АВС.
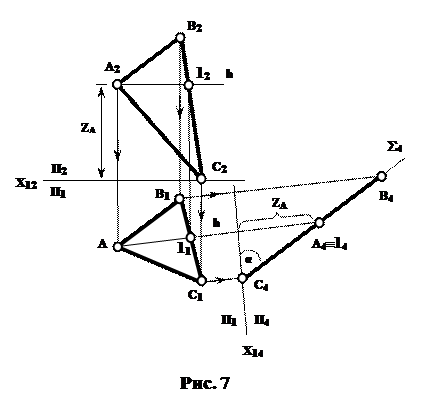 Якщо пряма h площини АВС перпен-дикулярна до площини проекцій, то й сама площина АВС буде перпендикулярною (проецюючою) до цієї площини проекцій. Тому П2 замінюємо на П4, перпендикулярну h1. Вісь Х14, у цьому випадку, буде перпен-дикулярною до h1. Площина П4 буде перпендикулярною до площини трикутника АВС. Проекцією å4 площини АВС на П4 буде пряма С4А4В4.
Якщо пряма h площини АВС перпен-дикулярна до площини проекцій, то й сама площина АВС буде перпендикулярною (проецюючою) до цієї площини проекцій. Тому П2 замінюємо на П4, перпендикулярну h1. Вісь Х14, у цьому випадку, буде перпен-дикулярною до h1. Площина П4 буде перпендикулярною до площини трикутника АВС. Проекцією å4 площини АВС на П4 буде пряма С4А4В4.
Кут α визначає кут нахилу площини трикутника АВС до П1. При перетворенні площини загального положення у проецюючу треба незмінною залишити П2, а П1 замінити на П4, перпендикулярну до її фронталі.
Площина å(fìüh) (рис.8) задана горизонталлю та фронталлю,
що перетинаються. Тому в цьому випадку вісь Х24 буде перпендикулярною f2, а сама площина å – перпендикулярною до П4.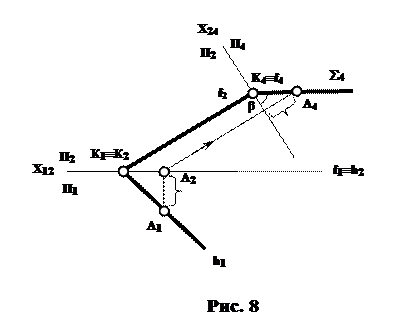 Кут між проекцією площини å4 та віссю Х24 визначає кут нахилу площини до П2.
Кут між проекцією площини å4 та віссю Х24 визначає кут нахилу площини до П2.
1.1.4. Перетворити площину загального положення на площину рівня (паралельну).
На рис. 9 площина задана трикутником АВС. Для перетворення її на площину рівня треба виконати подвійну заміну.
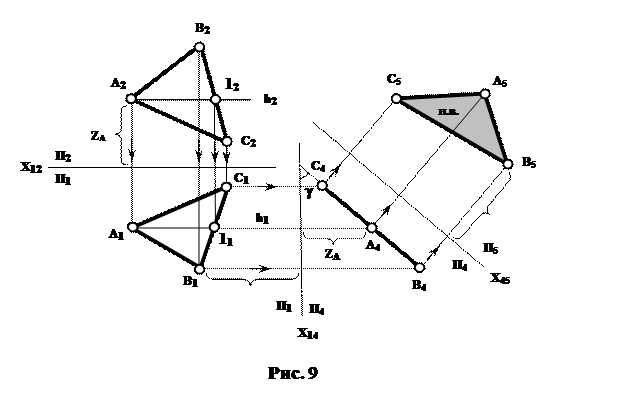 Спочатку в системі П1П4 площина АВС перетворюється на проецюючу А4В4С4. Вісь Х14 (горизонтальна проекція П4) буде перпендикулярною горизонталі h1 трикутника АВС. Потім П1 замінюємо на П5, паралельну трикутнику. Вісь Х45 (проекція П5 на П4) у цьому випадку буде паралельною С4А4В4, а сама площина АВС у системі П4П5 перетвориться на площину рівня.
Спочатку в системі П1П4 площина АВС перетворюється на проецюючу А4В4С4. Вісь Х14 (горизонтальна проекція П4) буде перпендикулярною горизонталі h1 трикутника АВС. Потім П1 замінюємо на П5, паралельну трикутнику. Вісь Х45 (проекція П5 на П4) у цьому випадку буде паралельною С4А4В4, а сама площина АВС у системі П4П5 перетвориться на площину рівня.
Таким чином, трикутник спроецювався на площину П5 без спотворення.
Для перетворення площини загального положення, замість розглянутої, на площину рівня, можна використати подвійну заміну площин П1 на П4, та П2 на П5.
1.2. Спосіб обертання.
Цей спосіб полягає в тому, що об'єкт проецювання за допомогою обертання навколо деякої осі займає відносно нерухомих площин проекцій положення більш зручне для розв'язання задач.
Усі точки об'єкта проецювання при обертанні навколо лінії, що приймається за вісь обертання, переміщуються по дугах кола. Ці дуги лежать у площинах, що перпендикулярні до осі обертання. За допомогою цього способу також є можливість вирішення чотирьох основних задач перетворення.
1.2.1.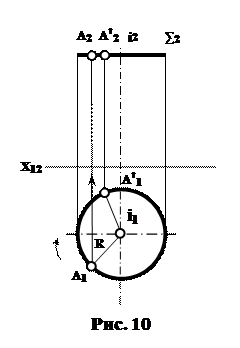 Обертання навколо осей, перпендикулярних до площин проекцій.
Обертання навколо осей, перпендикулярних до площин проекцій.
На рис. 10 наведено схему обертання точки А навколо осі обертання "і", перпендикулярної П1.
Площина Σ( Σ2) обертання точки А, у цьому випадку, буде паралельною П1, а тому, коло обертання радіуса R на П1 проецюється без спотворення.
 При обертанні точки А(А1, А2) на якийсь кут навколо вісі "і" її новими проекціями будуть А'1, А'2.
При обертанні точки А(А1, А2) на якийсь кут навколо вісі "і" її новими проекціями будуть А'1, А'2.
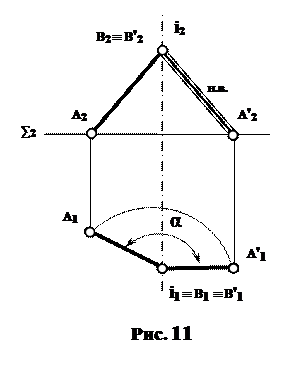
На рис. 11 зображено перетворення прямої загального положення на пряму рівня. Такого положення можна досягти обертаючи відрізок АВ навколо осі "і", перпендикулярної, наприклад, до П1. Всі точки прямої обертаються на один і той же кут в площинах перпендикулярних осі, а тому в площинах горизонтальних.
 Якщо потрібно пряму АВ загального положення перетворити на пряму рівня, то її горизонтальна проекція А1В1 під час обертання повинна зайняти положення (А'1В'1) паралельне осі Х. У цьому разі радіус Rбуде перпендикулярним осі Х.
Якщо потрібно пряму АВ загального положення перетворити на пряму рівня, то її горизонтальна проекція А1В1 під час обертання повинна зайняти положення (А'1В'1) паралельне осі Х. У цьому разі радіус Rбуде перпендикулярним осі Х.
Проекцію А'1В'1 визначимо завдяки постійній величині горизонтальної проекції. Відповідну нову фронтальну проекцію А'2В'2 визначимо за допомогою ліній проекційного зв'язку.
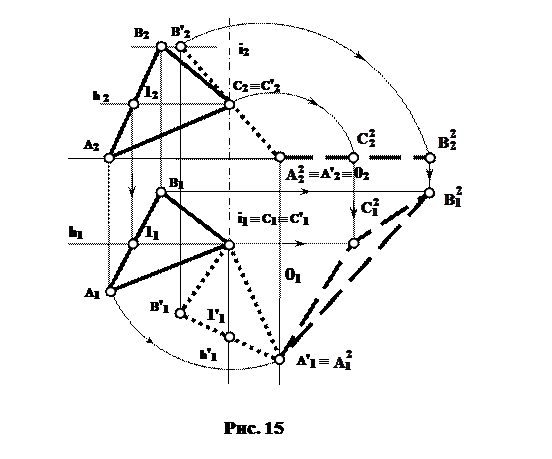 |
Перетворення площини загального положення на площину рівня виконується подвійним обертанням навколо осі "і" до положення проецюючого, а потім навколо осі "0" до положення рівня (
 ,
, 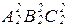 )(рис. 15).
)(рис. 15).
1.2.2. Обертання навколо ліній рівня.
Крім обертання навколо осей, перпендикулярних площинам проекцій, користуються обертанням навколо ліній рівня площин, якщо треба площину загального положення перетворити на площину рівня.
Це буває потрібно при визначенні натуральних розмірів плоских фігур. У довільній площині завжди можна вибрати одну з безлічі головних ліній, а потім обернути навколо цієї лінії задану площину до такого положення, щоб площина стала паралельною площині проекцій.
На рис. 16 зображено площину Σ (fìüh) загального положення, задану слідами. Для визначення величини плоского кута, що утворюється в просторі між слідами площини, виконано суміщення відсіку площини з площиною П1 (обертання площини навколо горизонталі "h").
 Віссю обертання у даному випадку служить горизонталь-ний слід площини – h1.
Віссю обертання у даному випадку служить горизонталь-ний слід площини – h1.
Для знаходження суміще-ного фронтального сліду, на ньому вибирають довільну точку А, яка при обертанні навколо горизонтального сліду h1, рухатиметься у вертикальній площині, перпендикулярній до h1. При цьому відстань від точки А до точки збігу слідів площини збережеться, що дозволить з точки збігу слідів провести дугу кола до перетину в точці А'2 з площиною траєкторії горизонтальної проекції точки. Суміщений фронтальний слід f '2 пройде через точку збігу слідів і знайдену точку А'2.
1.3. Спосіб плоскопаралельного переміщення.
Якщо при способі заміни площин проекцій геометричні фігури залишають на місці, а до них, певним чином, підбирають площини проекцій, то при способі плоскопаралельного переміщення роблять навпаки: площини проекцій П1 і П2 залишають незмінними, а геометричні образи (фігури) переміщують певним чином.
На рис. 10було наведено обертання точки А навколо осі "і", перпендикулярної П1. На протязі всього обертання точка А переміщується в площині Σ(Σ2), паралельній П1, та перпендикулярній до осі "і". Такі перетворення можна виконати і без зафіксованих осей, перпендикулярних площинам проекцій.
Так, на рис. 17 наведено плоскопаралельне переміщення точки А в площині рівня Σ (Σ2).
 Яке б положення не займала при переміщенні точка А, її фронтальні проекції завжди співпадають з проекцією Σ2.
Яке б положення не займала при переміщенні точка А, її фронтальні проекції завжди співпадають з проекцією Σ2.
Спосіб плоскопаралельного переміщення є обертанням навколо невиявлених осей, перпендикулярних до П1 і П2. Відповідно до цього виконується рішення основних задач перетворення. Так, на рис. 18 наведено переміщення прямої АВ в площинах Σ, Г (для точок А, В), паралельних П1, до положення паралельного П2. При цьому А1В1 = А'1В'1. Потім пряма АВ з положення рівня переміщена в площині Т(Т1) до проецюючого до П1 положення. Інші типові задачі виконуються аналогічно.
 |
1.4. Приклади розв'язання метричних та позиційних задач за допомогою способів перетворення проекцій.
1.4.1. Визначити відстань точки А від площини загального положення Σ (aìüb).
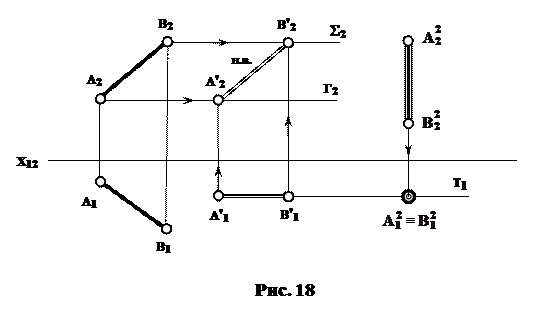
Рішення задачі наведено на рис. 19.
 |
Площина Σ (aìüb) заміною П2 на П4, яка перпендикулярна прямій "а", перетворюється на П4 на площину проецюючу (Σ4). Шукана відстань A4R4 визначається на П4, проведенням прямої A4R4 ^ Σ4. Її горизонтальна проекція A1R1 паралельна осі Х14.
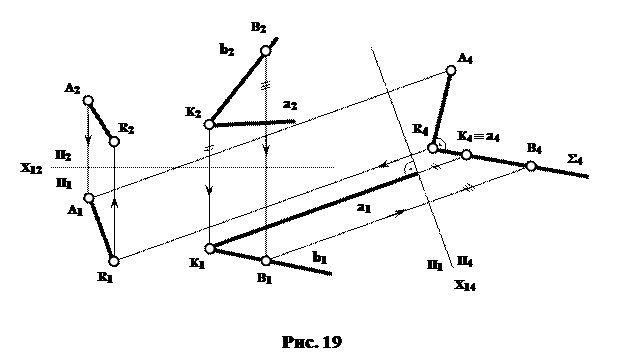
1.4.2. Визначити відстань точки А до прямої ВС
загального положення (рис 20).
 |
Ця відстань (АR) на кресленні визначається (А5R5) на площині П5, до якої пряма ВС буде проецюючою.
У системі П2П1 ця відстань (перпендикуляр з точки А на пряму ВС) визначиться зворотним ходом. При цьому A4R4 завжди паралельна Х45, так як перпендикуляр A5R5 є горизонтальною прямою.
1.4.3. Визначити відстань між мимобіжними
прямими АВ і CD.
Розв'язання задачі виконано на рис. 21 способом заміни площин проекцій. Заміна площин виконується відносно перетворення на П5 прямої АВ на проецюючу. Пряма CD під час перетворення замінюється прямою загального положення.
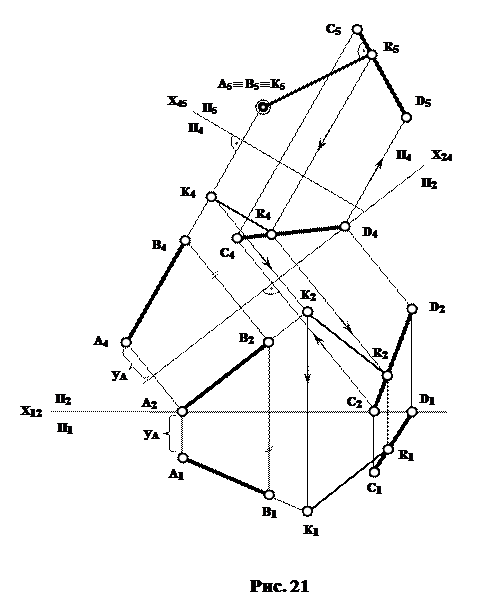 |
Відстань між мимобіжними прямими характеризується найкоротшою відстанню між двома (К,R) точками цих прямих. На площині П5 (К5R5) це перпендикуляр з А5ºВ5 на С5D5. Проекція К4R4 є паралельною осі Х45.
1.4.4. Визначити кут між прямими "a, b", які перетинаються (рис.22), подвійною заміною.
Площину АКВ перетворюємо на площину рівня відносно площини проекцій П5. А тому, шуканий кут між прямими
 |
спроецюється на П5 без спотворення. Це кут В5К5А5.
1.4.5. Визначити кут між прямою "а" та площиною загального положення Σ.
 Кут між прямою і площиною вимірюється кутом α (рис. 23) між прямою і її проекцією на цю площину.
Кут між прямою і площиною вимірюється кутом α (рис. 23) між прямою і її проекцією на цю площину.
У трикутнику АКВ кут β при вершині А доповнює кут αдо 90◦. Тому простіше знайти доповнюючий кут β між прямою "а" і перпендикуляром "d" з будь-якої точки прямої на площину Σ.
На рис. 24 це кут між прямими "а" і "b" при вершині А.
Перетворюючи проекції цього кута (площини) до положення, паралельного площині П5, визначимо дійсну величину кута α. Шуканий же кут α буде рівний 90◦ – β.
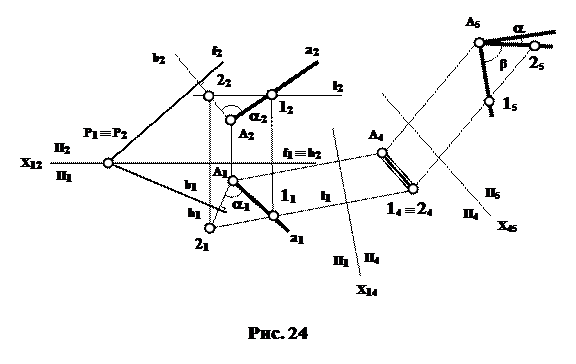 |
1.4.6. Визначити двогранний кут між площинами
Σ (DАВС) і T(DBCD).
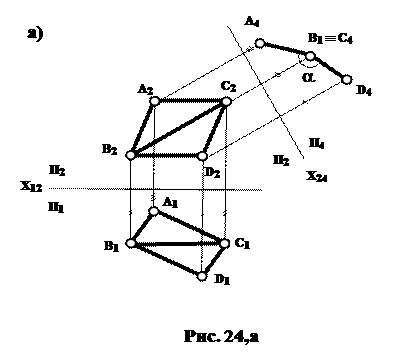 |
Цей кут вимірюється лінійним кутом, одержаним у результаті перетину двогранного кута площиною, перпендикулярною до його ребра.
На рис. 24, а ці дві площини вже мають лінію перетину. Це спільна пряма ВС – ребро двогранного кута. Тому, перетворивши креслення таким чином, щоб ребро ВС стало проецюючим, маємо величину лінійного кута a.
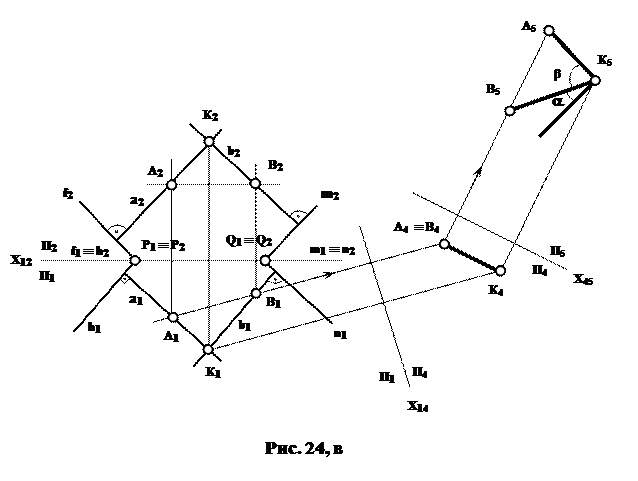
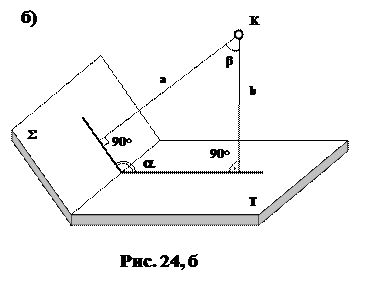 У деяких випадках, коли не визначене ребро двогранного кута, задача вирішується значно прості-ше, якщо визначити спочатку кут, що знахо-диться між перпендику-лярами "а" і "b" (рис. 24, б), опущеними з довільної точки К на задані площини. Кут між перпендикулярами "а" і "b" доповнює шуканий кут a до 180◦.
У деяких випадках, коли не визначене ребро двогранного кута, задача вирішується значно прості-ше, якщо визначити спочатку кут, що знахо-диться між перпендику-лярами "а" і "b" (рис. 24, б), опущеними з довільної точки К на задані площини. Кут між перпендикулярами "а" і "b" доповнює шуканий кут a до 180◦.
На рис. 24, в наведено приклад визначення двогранного кута a між площинами Σ (fìüh) і Т (mìün). Доповнюючий кут β визначається у трикутнику КАВ, сторони якого (КА і КВ), перпендикулярні до заданих площин Σ і Т. Спочатку визначаємо величину цього кута, а потім дійсного кута a, доповнюючи кут β до 90◦.
1.4.7. Визначити точки (К, R) перетину прямої АВ з
поверхнею сфери (рис. 25).

Рішення буде графічно точнішим, якщо посередник Σ, проведений через пряму АВ, перетне сферу по кривій "а", одна з проекцій якої – коло. Для цього треба перетворити проекції так, щоб пряма АВ стала прямою рівня.
1.4.8. Визначення проекцій та величини перерізу конуса
площиною Σ (аìüb) (рис. 26).
Замінивши площину П2 на П4 так, щоб площина перерізу Σ стала проецюючою (Σ4), будемо мати на П4 одну проекцію лінії перерізу. Вона буде співпадати з проекцією площини Σ4. Зворотним 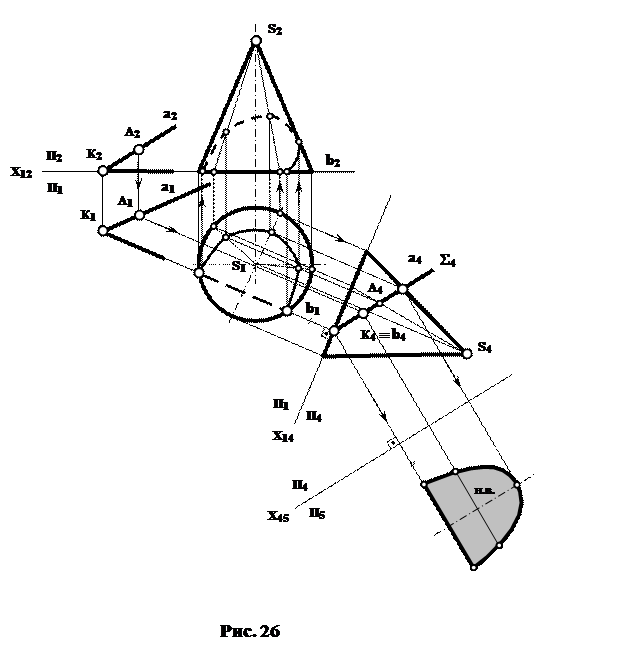 ходом визначаються проекції перерізу на П1, а потім на П2. Для знаходження дійсної величини плоскої фігури перерізу, виконується заміна П1 на П5, паралельну площині перерізу.
ходом визначаються проекції перерізу на П1, а потім на П2. Для знаходження дійсної величини плоскої фігури перерізу, виконується заміна П1 на П5, паралельну площині перерізу.
Усі наведені приклади виконані способом заміни площин проекцій. Але вони можуть бути виконані також і іншими способами перетворення проекцій, які були розглянуті раніше.
Л І Т Е Р А Т У Р А
1. В.Є. Михайленко, М.Ф. Євстіфєєв, С.М. Ковальов, О.В. Кащенко, Нарисна геометрія, К., НМКВО, 1991
2. В.Є. Михайленко, М.Ф. Євстіфєєв, С.М. Ковальов, О.В. Кащенко, Нарисна геометрія, К., "Вища школа", 1993
Читайте також:
- II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
- Аналіз комплексних статей витрат: витрат на утримання та експлуатацію устаткування, цехові, загальногосподарські, поза виробничі витрати.
- Білорусь. Характеристика положення та господарства країни.
- Бюджет може складатися із загального та спеціального фондів.
- Бюджетні кредити, надані за рахунок загального фонду державного бюджету
- Виберіть 2 положення, які треба добавити у визначення елементів наукової проблеми.
- Вибір між власним складом і складом загального користування
- Визначення вмісту загального та білкового азоту за методом Кьєльдаля
- Визначення загального трудового стажу
- Визначення положення газорідинних і водо-нафтових контактів
- Визначення поняття права. Значення загального поняття права. Різні підходи до визначення поняття права.
- Випарні апарати з горизонтальним і похилим положенням нагрівальних камер
| <== попередня сторінка | | | наступна сторінка ==> |
| Пряму загального положення перетворити | | | Переведення чисел із однієї позиційної системи числення в іншу |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |