
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Завдання для практичної роботи
Питання для самоконтролю
1. Як обчислюється кількісний еквівалент числа, заданого в позиційній системі числення?
2. В чому полягає суть методу безпосередньої заміни переведення числа із однієї системи числення в іншу? Коли його використовують?
3. В чому полягає алгоритм обчислень кількісного еквівалента за схемою Горнера? Який вигляд мають рекурентні формули для переведення: а) цілих чисел; б) дробових чисел?
4. Який вигляд має програма, реалізована засобами пакету Mathcad, яка реалізовує алгоритм безпосередньої заміни з використанням схеми Горнера у випадку переведення цілих і дробових чисел?
5. В чому полягає алгоритм ділення для переведення цілих чисел з системи числення з основою q в систему з основою p (q>p)?
6. В чому полягає алгоритм множення для переведення цілих чисел з системи числення з основою q в систему з основою p (q<p)?
7. В чому полягає алгоритм множення для переведення дробових чисел з системи числення з основою q=10в систему з основою p (p< q)?
8. В чому полягає алгоритм ділення для переведення дробових чисел з системи числення з основою p в систему з основою q=10 (p<q)?
9. Як визначається точність переведення дробових чисел з системи числення з основою q в систему з основою p?
10. Як здійснюється переведення чисел із системи числення з кратною основою?
11. Як здійснюється переведення чисел у симетричні і кососиметричні системи числення?
12. Як здійснюється переведення чисел із симетричних і кососиметричних систем у зміщені системи числення?
13. Як здійснюється переведення парних і непарних десяткових чисел у неканонічну двійкову систему числення з цифрами 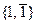 ?
?
14. Як здійснюється переведення з неканонічної двійкової системи числення у канонічну двійкову та десяткову?
15. В чому полягає алгоритм ділення для переведення цілих десяткових чисел в мінус-двійкову систему числення?
16. В чому полягає алгоритм множення для переведення дробових десяткових чисел в мінус-двійкову систему числення?
17. За яким алгоритмом здійснюється переведення змішаних десяткових чисел в мінус-двійкову систему числення?
18. За яким алгоритмом здійснюється переведення додатних десяткових чисел в мінус-двійкову систему числення?
19. За яким алгоритмом здійснюється переведення від’ємних десяткових чисел в мінус-двійкову систему числення?
20. Як здійснюється перехід від додатного числа, заданого в мінус-двійковій систем числення до від’ємного і навпаки?
21. Як здійснюється переведення з мінус-двійкової системи числення в канонічну двійкову систему?
22. В чому полягає алгоритм переведення чисел з десяткової системи числення в СЗК з використанням операції ділення?
23. В чому полягає алгоритм переведення чисел з десяткової системи числення в СЗК з використанням властивостей залишків?
24. В чому полягає метод ортогональних базисів переведення чисел з СЗК в десяткову систему?
25. В чому полягає метод переведення чисел з СЗК в десяткову систему з використанням поліадичної системи числення?
1. Користуючись алгоритмом безпосередньої заміни перевести задані числа 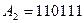 ,
, 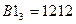 ,
, 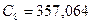 ,
, 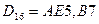 в десяткову систему числення.
в десяткову систему числення.
2. Користуючись схемою Горнера перевести задані числа, 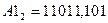 ,
, 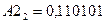 ,
, 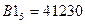 ,
,  ,
, 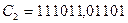 в десяткову систему числення.
в десяткову систему числення.
3. Нехай q=10, 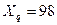 . Користуючись алгоритмом ділення “вручну” перевести задане число в системи числення з основами
. Користуючись алгоритмом ділення “вручну” перевести задане число в системи числення з основами 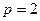 ,
, 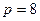 ,
, 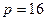 .
.
4. Нехай q=2, 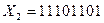 . Користуючись алгоритмом множення на основу числення q, починаючи з старшого розряду, перевести задане число в десяткову систему числення.
. Користуючись алгоритмом множення на основу числення q, починаючи з старшого розряду, перевести задане число в десяткову систему числення.
5. Перевести дріб 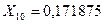 в двійкову та вісімкову системи числення користуючись алгоритмом множення відповідно на 2 та 8.
в двійкову та вісімкову системи числення користуючись алгоритмом множення відповідно на 2 та 8.
6. Перевести вісімкове і шістнадцяткове числа Х8=245,3076 і Y16=АF28,В3С в двійкову систему числення.
7. Перевести число Х2= 1111011011,1011011 із двійкової системи у вісімкову і шістнадцяткову системи числення.
8. В дев’ятковій системі числення з симетричною базою, додатні цифри якої зображаються арабськими цифрами, від’ємні арабськими цифрами рискою над ними, задано число 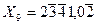 . Потрібно його перевести в трійкову систему з симетричною базою
. Потрібно його перевести в трійкову систему з симетричною базою 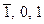 .
.
9. Число 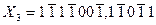 , задане в трійковій системі числення з симетричною базою, перевести в дев’яткову систему числення також з симетричною базою.
, задане в трійковій системі числення з симетричною базою, перевести в дев’яткову систему числення також з симетричною базою.
10. Перевести десяткове число 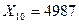 у канонічні трійкову та п’ятіркову системи числення.
у канонічні трійкову та п’ятіркову системи числення.
11. Перевести в зміщену десяткову систему число 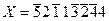 , задане в кососиметричній десятковій системі з цифрами {
, задане в кососиметричній десятковій системі з цифрами {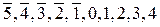 }.
}.
12. Перевести двійкові числа 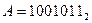 і
і 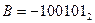 ,
, 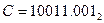 і
і  в систему з основою 2 і цифрами {1,
в систему з основою 2 і цифрами {1, }.
}.
13. Перевести в систему  числа
числа 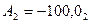 і
і 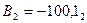 при
при 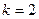 ,
, 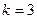 і
і 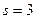 .
.
14. Користуючись методом діленням з остачею, перевести десяткові числа 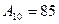 ,
, 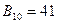 і
і 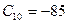 в мінус-двійкову систему числення.
в мінус-двійкову систему числення.
15. Користуючись методом множення на основу числення  , перевести десяткові дроби
, перевести десяткові дроби 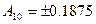 ,
, 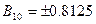 в мінус-двійкову систему числення.
в мінус-двійкову систему числення.
16. Перевести десяткові дроби 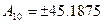 ,
, 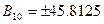 в мінус-двійкову систему числення.
в мінус-двійкову систему числення.
17. За допомогою методу розщеплення на складові перевести цілі десяткові числа 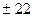 ,
, 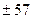 і
і 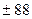 в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
18. За допомогою методу розщеплення на складові перевести десяткові дроби 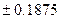 ,
, 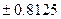 в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
19. За допомогою методу розщеплення на складові перевести мішані десяткові дроби  ,
, 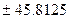 в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
в мінус-двійкову систему числення, попередньо перевівши їх в канонічну двійкову систему числення.
20. Для заданих чисел 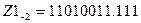 і
і 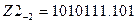 знайти числа протилежні за знаком. Виконати перевірку повторним перетворенням.
знайти числа протилежні за знаком. Виконати перевірку повторним перетворенням.
21. Перевести змішані дробові числа 110101.11 і 101110.111 з мінус-двійкової системи числення в двійкову.
22. Перевести десяткові числа 753 і 1135 в СЗК за модулями 
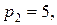
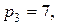
 користуючись методами: а) діленням з остачею; б) з використанням властивостей залишків.
користуючись методами: а) діленням з остачею; б) з використанням властивостей залишків.
23. Перевести в десяткову систему числа Х=(2,3,4,5) і Y=(0,2,4,7), подані в СЗК за модулями  .
.
24. Користуючись поданням десяткового числа в поліадичній системі, перевести число Х=(3,1,2,5) із СЗК з модулями 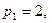
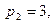
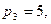
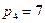 в десяткову канонічну систему .
в десяткову канонічну систему .
Читайте також:
- II. Вимоги безпеки перед початком роботи
- II. Вимоги безпеки праці перед початком роботи
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
- IV. Вимоги безпеки під час роботи на навчально-дослідній ділянці
- V. Завдання.
- VII. Прибирання робочих місць учнями (по завершенню роботи) і приміщення майстерні черговими.
- VІ. Підсумки уроку і повідомлення домашнього завдання.
- Адаптація персоналу: цілі та завдання. Введення у посаду
- Адвокатура в Україні: основні завдання і функції
- Аконність залишення засуджених у слідчому ізоляторі для роботи з господарського обслуговування.
| <== попередня сторінка | | | наступна сторінка ==> |
| З використанням поліадичної системи | | | Завдання для самостійної роботи |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |