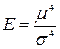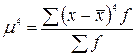РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лекція №4 – 5
Тема №7 « Аналіз рядів розподілу»
План лекції.
1. Показники центру розподілу;
2. Показники варіації;
3. Показники форми розподілу;
4. Моделювання розподілу.
В результаті зведення та групування одержують ряди розподілу. В залежності від статистичної природи групувальної ознаки (х) ряди розподілу розділяють на атрибутивні та варіаційні ( за кількісною ознакою). В свою чергу варіаційні ряди поділяються на інтервальні та дискретні. Ряди розподілу складаються із варіант(х) та частот f або часток d. Ряди розподілу з абсолютними частотами f характеризують склад сукупності, а з відносними(частками d) структуру сукупності. Якщо ряд розподілу є інтервальним з нерівними інтервалами то аналізуючи розподіл використовують щільність частоти( частки) на одиницю інтервалу :
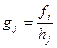 ;
; 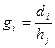
Ряди розподілу характеризуються моментами розподілу.
Моментом розподілу - називають середню арифметичну к-го степеня відхилення варіант х від сталого числа А. Загальний вигляд моментів:
 ,
,
Якщо А=0, отримує початкові моменти:
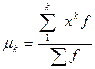 ,
,
Якщо А=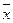 , отримаємо центральні моменти
, отримаємо центральні моменти
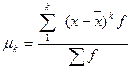 ,
,
Якщо  і
і 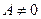 , отримаємо умовні моменти
, отримаємо умовні моменти
 .
.
Ряди розподілу характеризуються показниками центру розподілу, варіації та показниками форми розподілу.
До характеристикцентру розподілу відносять середню арифметичну зважену, а також порядкові середні: моду, медіану та інші квантилі.Середня арифметичнахарактеризує типовий рівень ознаки в сукупності. За даними ряду розподілу середня розраховується, як середня арифметична зважена:
| на основі частот | на основі часток |

|
Середня арифметична зазнає впливу всіх індивідуальних значень. Середня арифметична зважена – це початковий момент 1-го порядку.
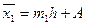 ;
;  - умовний момент 1-го порядку;
- умовний момент 1-го порядку;
 , А- довільне число , як правило це варіанта, яка має найбільшу частоту; h це розмір інтервалу групування.
, А- довільне число , як правило це варіанта, яка має найбільшу частоту; h це розмір інтервалу групування.
Приклад.№1Визначити середню величину кредитного портфеля банків.
| Групи банків за розміром кредитного портфеля (млн..грн.) | Число банків f | Середина інтервалу х | X*f | 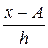
| (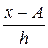 )f )f
| S |
| 5-10 | 7,5 | -2 | -8 | |||
| 10-15 | 12,5 | 62,5 | -1 | -5 | ||
| 15-20 | 17,5 | |||||
| 20-25 | 22,5 | 67,5 | ||||
| 25-30 | 27,5 | |||||
| Разом | -6 |
А=17,5; h=5
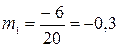 ;
; 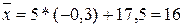 млн.грн.
млн.грн.
 млн.грн.
млн.грн.
Різновидом середніх величин є порядкові середні – це мода, медіана та інші квантилі.
Мода М0 –це найпоширеніше значення ознаки в рядах розподілу, тобто варіанта, яка в ряду розподілу має найбільшу частоту (частку).
У дискретному ряду М0 визначається візуально за максимальною частотою, або часткою.
Приклад №2.При аналізі проданого взуття, що до розміру взуття отримали наступні данні:
| Розмір взуття | Число проданих пар | S |
| Разом |
Мо=38 розмір.
В інтервальних рядах моду визначають за формулою Орженського:
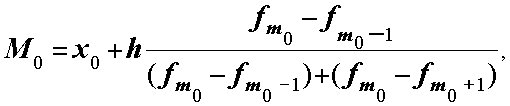 де x0 та h- відповідно нижня межа та ширина модального інтервалу.
fm0 , fm0-1, fm0+1 - частоти (частки) модального, передмодального та післямодального інтервалу.
Модальним називають інтервал, якому відповідає найбільша частота, він визначається візуально.
Приклад №3.Розрахуємо моду для кредитного портфеля банків за даними приклада №1. де x0 та h- відповідно нижня межа та ширина модального інтервалу.
fm0 , fm0-1, fm0+1 - частоти (частки) модального, передмодального та післямодального інтервалу.
Модальним називають інтервал, якому відповідає найбільша частота, він визначається візуально.
Приклад №3.Розрахуємо моду для кредитного портфеля банків за даними приклада №1.
 млн.грн.
Медіана Ме - це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини.
Для визначення Ме у ряду використовують кумулятивні ( нагромаджені) частоти Sf або Sd.
У дискретному ряду медіаною буде значення ознаки, для якої Sf ≥ 0,5. Якщо сукупність має непарну кількість елементів то Ме визначають за її номером. млн.грн.
Медіана Ме - це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини.
Для визначення Ме у ряду використовують кумулятивні ( нагромаджені) частоти Sf або Sd.
У дискретному ряду медіаною буде значення ознаки, для якої Sf ≥ 0,5. Якщо сукупність має непарну кількість елементів то Ме визначають за її номером. 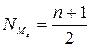 , де n= , де n= Якщо сукупність має парну кількість елементів, то медіану визначають, як середню арифметичну між двома середніми значеннями.
В нашому випадку
Якщо сукупність має парну кількість елементів, то медіану визначають, як середню арифметичну між двома середніми значеннями.
В нашому випадку  , отже 10 і 11 пара будуть припадати на 38 розмір, відповідно медіаною буде 38 розмір.
Вінтервальному ряду медіана визначається за формулою Фехнера: , отже 10 і 11 пара будуть припадати на 38 розмір, відповідно медіаною буде 38 розмір.
Вінтервальному ряду медіана визначається за формулою Фехнера:
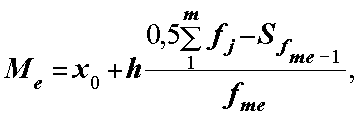 де x0 та h – нижня межа та розмір медіального інтервалу;
Sme-1 – кумулятивна частота предмедіального інтервалу;
fme- частота медіального інтервалу.
Приклад№4. За даними приклада №1 розрахуємо медіальне значення для кредитного портфеля банків.
де x0 та h – нижня межа та розмір медіального інтервалу;
Sme-1 – кумулятивна частота предмедіального інтервалу;
fme- частота медіального інтервалу.
Приклад№4. За даними приклада №1 розрахуємо медіальне значення для кредитного портфеля банків. 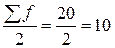 , отже оскільки кумулятивна частота третього інтервалу відповідає умові Sf ≥ 0,5, то третій інтервал є медіальним, х 0= 15, Sme-1= 9, fme= 6, h= 5. , отже оскільки кумулятивна частота третього інтервалу відповідає умові Sf ≥ 0,5, то третій інтервал є медіальним, х 0= 15, Sme-1= 9, fme= 6, h= 5.
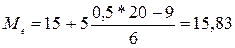 . Отже половина досліджених банків мають кредитний портфель до 15,83 млн.грн., а друга половина більше 15,83 млн. грн.
До структурних показників рядів розподілу відносяться квартилі, децилі і просентеміллі.
Квартилі Q — це значення варіант, які ділять упорядкований ряд за обсягом сукупності на чотири рівних частини,а децилі D – на десять рівних частин. Просетеміллі на сто.
Отже, в ряду розподілу визначаються три квартилі та дев’ять децилів. Медіана є водночас другим квартилем та п’ятим децилем. Розрахунок квартилів та децилів грунтується на кумулятивних частотах (частках).
Для дискретних упорядкованих рядів квартилі визначаються:
Перша квартіль буде відповідати ознака з номером . Отже половина досліджених банків мають кредитний портфель до 15,83 млн.грн., а друга половина більше 15,83 млн. грн.
До структурних показників рядів розподілу відносяться квартилі, децилі і просентеміллі.
Квартилі Q — це значення варіант, які ділять упорядкований ряд за обсягом сукупності на чотири рівних частини,а децилі D – на десять рівних частин. Просетеміллі на сто.
Отже, в ряду розподілу визначаються три квартилі та дев’ять децилів. Медіана є водночас другим квартилем та п’ятим децилем. Розрахунок квартилів та децилів грунтується на кумулятивних частотах (частках).
Для дискретних упорядкованих рядів квартилі визначаються:
Перша квартіль буде відповідати ознака з номером  ,
третій квартилі відповідає ознака з номером ,
третій квартилі відповідає ознака з номером  Для вирохування кварти лей застосовують наступні правила:
1. Якщо індекс квартилі задається цілим числом, значенням квартилі рахується елемент з вказаним індексом;
2. Якщо індекс квартилі задається величиною, яке є середньою величиною з двох цілих чисел, квартіль дорівнює середньому арифметичному, яке вираховується з елементів, індекси яких дорівнюють цим числам .
3. Якщо індекс квартилі задається величиною, яке не цілим числом і не кратна 1/2, воно закруглюється до найближчого цілого.
Для вирохування кварти лей застосовують наступні правила:
1. Якщо індекс квартилі задається цілим числом, значенням квартилі рахується елемент з вказаним індексом;
2. Якщо індекс квартилі задається величиною, яке є середньою величиною з двох цілих чисел, квартіль дорівнює середньому арифметичному, яке вираховується з елементів, індекси яких дорівнюють цим числам .
3. Якщо індекс квартилі задається величиною, яке не цілим числом і не кратна 1/2, воно закруглюється до найближчого цілого.

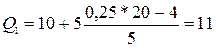

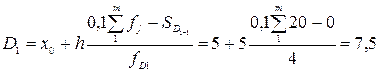
 Варіація - це мінливість, коливання, різноманітність значень ознаки (у) одиниць сукупності під дією різних чинників.
Варіація, яка виникає під впливом суттєвих чинників і має систематичний характер( спостерігається послідовна зміна варіантів ознак в визначеному напрямку) називається систематичною варіацією .
Варіація, яка виникає під дією випадкових факторів , називається випадковою варіацією.
Варіація ознаки у під дією всіх чинників називається загальною варіацією.
Показники варіації використовують для:
- вивчення закономірностей розподілу;
- оцінки взаємозв’язку між ознаками;
- проведення вибіркових спостережень;
- оцінки ступеня однорідності сукупності (чим меншою є варіації, тим більш однорідною є сукупність);
- міжрегіональних та міжнародних порівнянь.
Для вимірювання та оцінки розміру варіації використовується система статистичних показників:
1. Розмах варіації (R), що характеризує максимальну амплітуду коливань значень ознаки у сукупності:
R = Хmax – Хmin,
де Хmax, Хmin — відповідно найбільше та найменше значення ознаки у сукупності.
В інтервальних рядах розподілу розмах варіації визначається як різниця між верхньою межею останнього та нижньою межею першого інтервалу. Перевагою даного показника є простота обчислення та ясність економічної інтерпретації. Головний недолік полягає у тому, що він визначається лише по двох граничних величинах, які часто є випадковими, та не дає уявлення про ступінь варіації в середині сукупності. . Квартильний розмах.
Варіація - це мінливість, коливання, різноманітність значень ознаки (у) одиниць сукупності під дією різних чинників.
Варіація, яка виникає під впливом суттєвих чинників і має систематичний характер( спостерігається послідовна зміна варіантів ознак в визначеному напрямку) називається систематичною варіацією .
Варіація, яка виникає під дією випадкових факторів , називається випадковою варіацією.
Варіація ознаки у під дією всіх чинників називається загальною варіацією.
Показники варіації використовують для:
- вивчення закономірностей розподілу;
- оцінки взаємозв’язку між ознаками;
- проведення вибіркових спостережень;
- оцінки ступеня однорідності сукупності (чим меншою є варіації, тим більш однорідною є сукупність);
- міжрегіональних та міжнародних порівнянь.
Для вимірювання та оцінки розміру варіації використовується система статистичних показників:
1. Розмах варіації (R), що характеризує максимальну амплітуду коливань значень ознаки у сукупності:
R = Хmax – Хmin,
де Хmax, Хmin — відповідно найбільше та найменше значення ознаки у сукупності.
В інтервальних рядах розподілу розмах варіації визначається як різниця між верхньою межею останнього та нижньою межею першого інтервалу. Перевагою даного показника є простота обчислення та ясність економічної інтерпретації. Головний недолік полягає у тому, що він визначається лише по двох граничних величинах, які часто є випадковими, та не дає уявлення про ступінь варіації в середині сукупності. . Квартильний розмах.
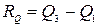 , охоплює 50% обсягу сукупності,
Децільний розмах. , охоплює 50% обсягу сукупності,
Децільний розмах.
 , охоплює 80% обсягу сукупності.
На практиці широко використовуються характеристики, що ґрунтуються на відхиленні індивідуальних значень від середньої величини , охоплює 80% обсягу сукупності.
На практиці широко використовуються характеристики, що ґрунтуються на відхиленні індивідуальних значень від середньої величини  2.Середнє лінійне відхилення (l), що характеризує середній розмір коливань значень ознаки навколо середнього рівня .
Просте середнє лінійне відхилення визначається по незгрупованих даних
2.Середнє лінійне відхилення (l), що характеризує середній розмір коливань значень ознаки навколо середнього рівня .
Просте середнє лінійне відхилення визначається по незгрупованих даних
 , а зважене середнє лінійне відхилення по згрупованим даним
, а зважене середнє лінійне відхилення по згрупованим даним
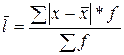 3.Дисперсія — це середній квадрат відхилень значень ознаки від середнього рівня:
Для не згрупованих даних Для згрупованих даних
3.Дисперсія — це середній квадрат відхилень значень ознаки від середнього рівня:
Для не згрупованих даних Для згрупованих даних
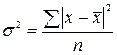  Термін дисперсія в перекладі з латинської мови означає розсіювати. Дисперсія величина не іменована.
Дисперсія служить не тільки показником варіації, але використовується при вимірюванні взаємозв’язків, перевірки гіпотез, при вибірковим спостереженні тощо.
Дисперсія, як і будь яка середня, має математичні властивості:
1. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А дисперсія не зміниться;
2. Якщо всі варіанти помножити на будь-яке число k то дисперсія збільшиться в k2;
3. У разі заміни частот частками дисперсія не зміниться.
Скориставшись математичними властивостями дисперсії в інтервальних рядах з рівними інтервалами дисперсію можна визначити методом «моментів» за формулою:
Термін дисперсія в перекладі з латинської мови означає розсіювати. Дисперсія величина не іменована.
Дисперсія служить не тільки показником варіації, але використовується при вимірюванні взаємозв’язків, перевірки гіпотез, при вибірковим спостереженні тощо.
Дисперсія, як і будь яка середня, має математичні властивості:
1. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А дисперсія не зміниться;
2. Якщо всі варіанти помножити на будь-яке число k то дисперсія збільшиться в k2;
3. У разі заміни частот частками дисперсія не зміниться.
Скориставшись математичними властивостями дисперсії в інтервальних рядах з рівними інтервалами дисперсію можна визначити методом «моментів» за формулою:
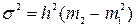 , де , де 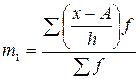 , , 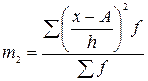 Приклад.№5Визначити середню величину кредитного портфеля банків.
Приклад.№5Визначити середню величину кредитного портфеля банків.
А=17,5; h=5
Дисперсію обчислюють також за способом різниці квадратів.
Для згрупованих Якщо ряд розподілу представлено якісною ознакою, яка має 2 взаємовиключні значення (альтернативи) – «1» і «0», а розподіл характеризується 2 частками – d1 , d0 дисперсія розраховується, як добуток часток 5. Середнє квадратичне відхилення (σ) — показує, на скільки в середньому відхиляються значення ознаки від середнього рівня: Для не згрупованих даних Для згрупованих даних
Величина іменована. Середнє квадратичне відхилення найчастіше використовується у статистичному аналізі, тому його називають стандартним відхиленням. Зрозуміло, що чим меншою є його величина, тим слабкішою є варіація і більш однорідною - статистична сукупність. Властивості середнього квадратичного і середнього лінійного відхилення. 1. 2. У симетричному, близькому до нормального розподілу . 6. Квартильне відхилення :
Для порівняння варіації різних ознак використовують відносні показники варіації : - коефіцієнт осциляції: VR = - лінійний коефіцієнт варіації: - квадратичний коефіцієнт варіації: Vσ = Vσ – вживається для оцінки однорідності сукупності. Вважається, що сукупність є однорідною, якщо V £ 33 % .Крім цього, наведений коефіцієнт варіації застосовують для оцінки ступеня варіації: V < 15% — слабка; 15 £ V £ 25% — середня; V > 25% — сильна. - квартильний коефіцієнт варіації
- децильний коефіцієнт варіації :
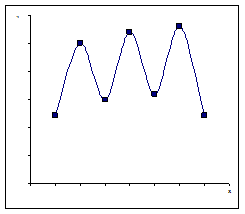
VD використовують в міжнародній статистиці для розрахунку 10% доходів найбагатших людей в країні та 10% найбідніших людей в країні . В розвинутих країнах цей показник має бути не більше 7, якщо він наближається до 10 ситуація вважається загрозливою. Характеристики форми розподілу. При вивченні форми розподілу в залежності від значень частот розрізняють одно-, дво- та багатовершинні ряди розподілу. Якісно однорідні сукупності мають одновершинний (одномодальний) розподіл одиниць. Наявність декількох вершин свідчить про неоднорідність сукупності. .
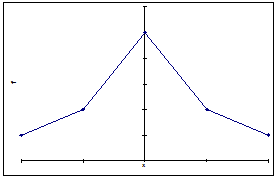
Багатовершинний розподіл Одновершинний розподіл. Серед одновершинних рядів розподілу розрізняють симетричні та асиметричні, гостро- та плосковершинні. У симетричних рядах розподілу середня арифметична, мода і медіана співпадають.
Якщо
Якщо
Напрямок та міру асиметрії характеризують відносними показниками асиметрії, які обчислюються за формулами: При правосторонній асиметрії А > 0, при лівосторонній А < 0, при симетричному розподілі А = 0. Вважається, що при |A| < 0,25 асиметрія слабка, при 0,25<|A|<0,5 – середня, при |A| > 0,5 – сильна. Асиметрія виникає в наслідок обмеженої варіації в одному напрямку. Для порівняння ступеня скошеності використовують момент 3-го порядку розраховують коефіцієнти асиметрії:
Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини і називається ексцесом. За ексцесом поділяють розподіл на гостровершиний і плосковершиний.
|
Гостровершиний Е >3 Плосковершиний Е <3
В симетричних рядах близьких до нормального Е =3 . Для вимірювання ексцесу використовується стандартизований момент 4-го порядку :
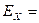
 , де
, де 
За допомогою середньої квадратичної похибки асиметрії  і середньої квадратичної похибки ексцесу
і середньої квадратичної похибки ексцесу 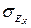 встановлюється істотність кожного з цих показників для розподілу ознаки в генеральній сукупності. Якщо :
встановлюється істотність кожного з цих показників для розподілу ознаки в генеральній сукупності. Якщо :
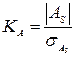 >3, де
>3, де  , то асиметрія істотна і розподіл ознаки в генеральній сукупності несиметричний.( n- кількість одиниць сукупності).
, то асиметрія істотна і розподіл ознаки в генеральній сукупності несиметричний.( n- кількість одиниць сукупності).
Якщо виконується умова :
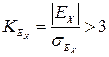
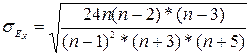 то ексцес є властивим для генеральної сукупності.
то ексцес є властивим для генеральної сукупності.
Закономірність розподілу одиниць сукупності за значеннями варіючої ознаки можна описати певною функцією, яка має назву теоретичної кривої розподілу. Серед безлічі кривих розподілу найбільш часто зустрічається нормальна крива розподілу, а сам розподіл, котрий можна описати цією кривою, має назву нормального розподілу. Він має наступні властивості:







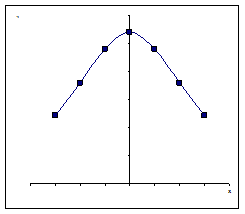
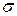
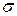
1. Крива симетрична відносно шкали ординат, а максимальна ордината відповідає значенню  ;
;
2. Крива асимптотично наближається до осі абсцис, продовжуючись в дві сторони до безкінечності;
3. крива має дві точки перетину з віссю абсцис , які знаходяться від  на відстані
на відстані  ;
;
4. Якщо  , то із збільшенням
, то із збільшенням 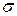 крива стає більш пологою. Якщо
крива стає більш пологою. Якщо 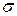 = const , то із зміною
= const , то із зміною  крива не змінить своєї форми, а лише зсуватиметься праворуч або ліворуч по вісі абсцис;
крива не змінить своєї форми, а лише зсуватиметься праворуч або ліворуч по вісі абсцис;
5.В межах ± σ знаходяться 68,3% одиниць сукупності; в межах ± 2σ - 95,5% ; 99,7% — в межах ± 3σ.
Останній запис називають правилом трьох сигм -згідно з цим правилом вірогідно, що нормально розподілена випадкова величина практично може відхилятися від свого середнього квадратичог значення не більше, ніж на потроєне середнє квадратичне відхилення.
Криву розподілу використовують для наближеного моделювання розподілу. Моделювання зводиться до вирівнювання емпіричного ряду розподілу за нормальною кривою. Суть вирівнювання полягає у знаходженні теоретичних частот на основі емпіричних даних при цьому використовуються стандартна функція нормального розподілу.
Якщо для вирівнювання ряду розподілу використовується диференційна функція Лапласа: 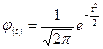 , то тоді теоретичні частоти визначаються за формулою:
, то тоді теоретичні частоти визначаються за формулою: 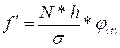 ,
,
де N = Σf – обсягу сукупності, або сума частот варіаційного ряду;
h – інтервал групування;
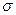 - середнє квадратичне відхилення.
- середнє квадратичне відхилення.
Функція 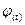 також табульована і її значення знаходимо в таблицях, попередньо визначивши нормовані відхилення
також табульована і її значення знаходимо в таблицях, попередньо визначивши нормовані відхилення 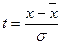 , де х – середина інтервалу групування.
, де х – середина інтервалу групування. 
Якщо для вирівнювання розподілу використовується інтегральна функція Лапласа: 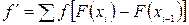 , де
, де
F(x) = 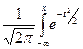 dt - інтегральна функція нормального розподілу Лапласа, яка табульована. Функція F(x) ґрунтується на стандартизованих відхиленнях.
dt - інтегральна функція нормального розподілу Лапласа, яка табульована. Функція F(x) ґрунтується на стандартизованих відхиленнях.
t = , де
, де  - верхня межа інтервалу групування. при від’ємних значеннях t, функція становить: F (-t) = [ 1 – F(x) ].
- верхня межа інтервалу групування. при від’ємних значеннях t, функція становить: F (-t) = [ 1 – F(x) ].
Для об’єктивного судження про відповідність емпіричного розподілу кривій нормального розподілу використовуються спеціальні критерії відповідності (Пірсона, Колмогорова, Ястремського та ін.).
1.Критерій Пірсона ( Хі-квадрат) визначається за формулою:
 ,де
,де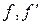 -емпіричні та теоретичні частота відповідно. Значення χ2 табульовані для ймовірності 1 -
-емпіричні та теоретичні частота відповідно. Значення χ2 табульовані для ймовірності 1 -  та числа ступенів волі k = m–r-1, де m – число груп, r- число параметрів( для нормальної кривої r=2(
та числа ступенів волі k = m–r-1, де m – число груп, r- число параметрів( для нормальної кривої r=2(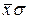 )). У тому випадку, коли χ2 < χ2таб, розподіл можна вважати наближено нормальним, а при χ2 > χ2таб — навпаки, розподіл не можна вважати наближеним до нормального.
)). У тому випадку, коли χ2 < χ2таб, розподіл можна вважати наближено нормальним, а при χ2 > χ2таб — навпаки, розподіл не можна вважати наближеним до нормального.
2. Критерій Колмогорова обчислюється за формулою:
λ = 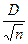 , де D = max |
, де D = max |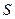 -
-  |;
|;
Із спеціальних таблиць ймовірностей для λ знаходять величину р(λ). Якщо це значення близьке до нуля — розподіл не можна вважати наближено нормальним, якщо р(λ) прямує до 1 — розподіл нормальний.
Читайте також:
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вид заняття: лекція
- Вступна лекція
- Вступна лекція 1. Методологічні аспекти технічного регулювання у
- Клітинна селекція рослин.
- Колекція фонограм з голосами осіб, які анонімно повідомляли про загрозу вибуху
- ЛЕКЦІЯ (4): Мануфактурний період світової економіки
- Лекція - Геополітика держави на міжнародній арені
- Лекція 02.04.2013
| <== попередня сторінка | | | наступна сторінка ==> |
| Ігри ХХІХ Олімпіади, Пекін, 8 серпня – 24 серпня 2008 р. | | | Критерій згоди Романовського |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |



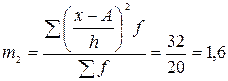
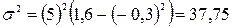

 для не згрупованих даних,
для не згрупованих даних,
 ,для альтернативної ознаки
,для альтернативної ознаки 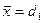
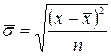
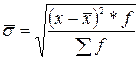
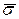 >
> .
.
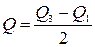
 100 %
100 %
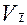 =
=  100 %
100 %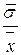 100
100 =
=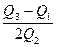
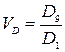

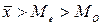 то маємо правосторонню асиметрію. AS >0 Е >3
то маємо правосторонню асиметрію. AS >0 Е >3
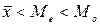 маємо лівосторонню асиметрію. AS <0 Е <3.
маємо лівосторонню асиметрію. AS <0 Е <3.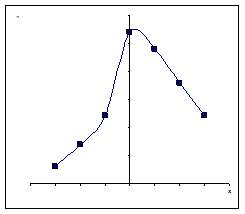

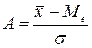

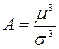
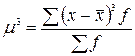 ;
;