• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Методи оптимізації систем із рециклом

Системи із зворотним зв'язком, або рециклом, часто застосовуються в тих випадках, коли ступінь вилучення продукту з сировини чи вихідна реакція при одноразовому проходженні ланцюга послідовних апаратів виявляються дуже малими. Тоді частина продукту з виходу останнього апарату ланцюга прямує на вхід першого апарату і знову проходить всю послідовність апаратів. Частка продукту, що повертається на вхід першого апарату, називається ступенем рециркуляції.

…

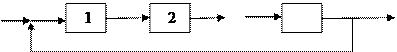
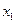
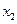Рис. 19. Система послідовно сполучених апаратів з рециклом

У послідовності ланок із зворотним зв'язком (рис. 19) вхід системи позначений , а вихід — . Постановка задачі керування не відрізняється від такої в системі послідовно сполучених ланок: знайти такі керуючі впливи 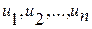,які б забезпечували максимум цільової функції:

за умов

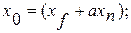
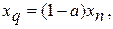
де — ступінь рециркуляції.

Умови для 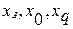являють собою рівняння зворотного зв'язку.

Оптимізація послідовності ланок із рециклом у ряді випадків може бути легко зведена до оптимізації послідовності апаратів без рецикла. Якщо вхідні і вихідні змінні схеми вільні, то задачу оптимізації розв¢язують для відповідної розімкненої схеми з вільним входом і виходом, а потім визначають значення вхідних і вихідних змінних за формулами:

.

Якщо вхідні і вихідні змінн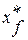і і 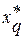задані, завдання керування зводиться до оптимізації розімкненої схеми із заданими входом і виходом :

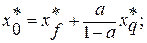
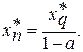
Коли вхідні змінні вільні, а вихідні задані, завдання оптимізації також зводиться до аналогічного завдання для розімкненої схеми. Тільки один варіант, а саме той, коли вхідні змінні задані, а вихідні вільні, не зводиться до задач оптимізації відповідної розімкненої схеми. Для рішення цієї задачі можуть бути використані методи динамічного програмування, принцип максимуму і ін.

Розрахунок може здійснюватися за методом розриву зворотних зв'язків. Ідея методу розриву зворотних зв'язків полягає в тому, що зворотний зв'язок умовно розривається, величини 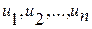і 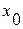вважають незалежними змінними, а керування зв'язку — обмеженням у формі рівності, накладеним на варійовані параметри. Далі розрахунок ведеться за будь-яким методом, що застосовується для розрахунку систем послідовної структури.

Розглянемо послідовність екстракторів, охоплених зворотним зв'язком. На вхід системи надходить 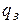м³/год розчину. У кожен екстрактор надходить м³/год води, яка виходить з екстрактора з концентрацією відмиваючої речовини 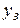. Приймемо, що в екстракторі досягається рівновага, тобто [де 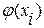- рівняння кривої рівноваги]. Частина готового продукту 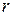м³/год повертається з виходу останньої ланки на вхід першої.

Рівняння зміщення (зворотному зв'язку)

(12)

Цільова функція, як і в раніше розглянутому прикладі,

,

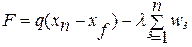де — відносна вартість води.

Якщо для вирішення завдачі використовувати метод розриву зворотного зв'язку, то функція Лагранжа має вигляд

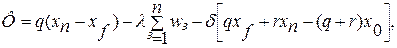
де — невизначений множник Лагранжа. Після перетворення отримуємо

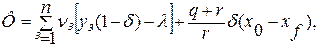
де перший член справа характеризує дохід в системі без зворотного зв'язку, що залежить від множника .

Для вирішення даної задачі оптимізації необхідно наступне: 1) знайти оптимальне керування, що залежить від параметра для розімкненої системи;

2) знайти 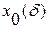, що забезпечує максимум Ф; 3) підставивши , і 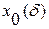в рівняння змішення, знайти , що забезпечує виконання рівності (12).

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. II. Бреттон-Вудська система (створена в 1944 р.)
6. III етап. Системний підхід
7. IV. Розподіл нервової системи
8. IV. Система зв’язків всередині центральної нервової системи
9. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
10. IV. Філогенез кровоносної системи
11. OSI - Базова Еталонна модель взаємодії відкритих систем
12. POS-системи

Переглядів: 653