• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Методи керування системою послідовно працюючих апаратів

Методи оптимізації систем із ре циклом.

Методи керування системою послідовно працюючих апаратів.

План

Системи послідовно з’єднаних ланок широко поширені в харчовій промисловості. При цьому можуть послідовно з'єднуватися апарати одного (наприклад, екстрактори) або різних (наприклад, теплообмінник, реактор, екстрактор і т. д.) типів. У системі послідовно з¢єднаних ланок (рис. 18) вектор входу в i-у ланку позначений вектор виходу —.

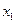
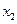
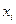
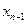
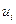
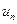
Рис. 18. Система послідовно з¢єднаних апаратів

Завдання керування ставиться таким чином: знайти керуючі впливи 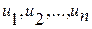, що забезпечують максимум цільової функції для системи послідовно з¢єднаних апаратів

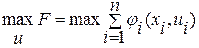(11)

за умов

.

Вибір методу рішення задачі (11) залежить від виду цільової функції 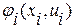і моделі апарату, тобто:

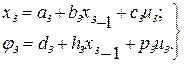
то задача керування виявляється задачею лінійного програмування. Якщо ж моделі і цільові функції нелінійні, то рішення задачі керування системою послідовних апаратів виявляється більш складнішим. Найбільш загальний метод рішення цих задач — метод динамічного програмування. Максимум цільової функції при цьому визначається послідовним застосуванням рекурентної формули Беллмана. Послідовність розрахунку залежить від того, яка величина (вхід системи 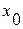або вихід системи 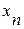) заздалегідь задана.

Розглянемо керування системою послідовної структури.

Нехай необхідно оптимально керувати системою, що складається з n послідовно з¢єднаних масообмінних апаратів — екстракторів. У екстрактор надходить 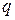м³/год розчину. Концентрація відмиваючої речовини на вході в екстрактор , на виході з i-го екстрактора . Керуючою змінною на кожній кроці є витрата промивної води . Концентрація речовини, що промивається, в промивній воді, що виходить з i-гo екстрактора, .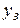

Припустимо, що в екстракторі досягається рівновага, тобто . Ефективність процесу визначається сумарною кількістю речовини, що вилучається з розчину. Витрати пов'язані з витратою промивної води. Цільова функція — дохід установки

,

де 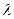— відносна вартість води.

Використовуючи рівняння матеріального балансу для кожного екстрактора , записуємо цільову функцію у вигляді

,

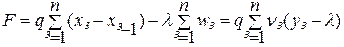де

Задача розв’язується методом динамічного програмування. Оптимізація проводиться від кінця на початку процесу. Якщо рівняння кривої рівноваги лінійне, тобто 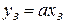, то задача оптимізації може бути розв’язана аналітично. При цьому витрата води через всі екстрактори буде однаковою, тобто

Читайте також:

1. D-тригер з динамічним керуванням
2. Автократично-демократичний континуум стилів керування.
3. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
4. Автоматизація меліоративних помпових стацій. Автоматизація керування помповими агрегатами.
5. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
6. Агресивне керування портфелем акцій
7. Адаптовані й специфічні методи дослідження у журналістикознавстві
8. Адміністративні (прямі) методи регулювання.
9. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
10. Адміністративні методи управління
11. Адміністративні, економічні й інституційні методи.
12. Адміністративно-правові (організаційно-адміністративні) методи мотивації

Переглядів: 676