• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок ступеня окиснення

Речовини, що в окисно-відновних реакціях втрачають електрони, називаються відновниками, а речовини, що приєднують електрони, – окисниками.

Висновок. Зазначена вище еволюція суспільних функцій держави торкається в тій чи іншій мірі усі без винятку, сучасні держави. Разом з тим відбувається еволюція функцій, що охоплює лише окремі держави, особливо в економічній сфері, зокрема тоді, коли конкре­тні суспільства розвиваються в напрямку ринкової економіки, переходять від соціалістичних, розподільних відносин до товарно-грошових, від тоталітарних режимів до ліберально-демократичних.

[1] Фома Аквінський був першим просвітителем нашої доби (від народження Христа) , хто заклав підвалини не схоластичного, а наукового пояснення реального світу завдяки використанню вчення древніх філософів.

[2] Держава, як суспільна організація, по своїй сутності була створена в першу чергу як соціальний інститут, направлений на забезпечення життєдіяльності людей.

[3] В соціально-економічній науці можна навести приклади двозначного трактування сутності категорій, які вживаються для пояснення суспільних явищ. Так, зокрема, можна стверджувати одяг заробітна плата є доходом, як і доходи це також заробітна плата у вузькому розумінні. В той же час, доходи людей включають не тільки заробітну плату, а й проценти, дивіденди, ренту тощо.

4 Геродот. История в девяти книгах. - Л., 1982 с. 164-166

⁷ Конституція України. Офіційне видання Ст.2

Для обчислення ступеня окиснення елемента слід враховувати наступні положення:

1. Ступінь окиснення атомів у простих речовинах дорівнює нулю (,).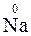

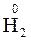2. Алгебраїчна сума ступенів окиснення всіх атомів, що входять до складу молекули, завжди дорівнює нулю, а в складному йоні ця сума дорівнює заряду йона.

3. Постійний ступінь окиснення мають атоми: лужних металів (+1), лужноземельних металів (+2), Гідрогену (+1) (крім гідридів NaH, CaH₂ і ін., де ступінь окиснення Гідрогену –1), Оксигену (–2) (крім F₂O і пероксидів, що містять групу –O–O–, у якій ступінь окиснення Оксигену –1).

4. Для елементів позитивний ступінь окиснення не може перевищувати величину, яка дорівнює номеру групи періодичної системи. Наприклад: ; ; ; ; .

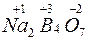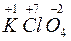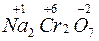Читайте також:

1. II. За зміною ступенів окиснення елементів, які входять до складу реагуючих речовин
2. Автоматичний розрахунок суми проведення.
3. Аеродинамічний розрахунок
4. Аеродинамічний розрахунок ротора вітроустановки
5. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
6. Аналітичний розрахунок завантаження горловин
7. Аналітичний розрахунок сумарного завантаження типових перетинань
8. Види норм праці, їх розрахунок
9. ВИЗНАЧЕННЯ НЕОБХІДНОГО СТУПЕНЯ ОЧИЩЕННЯ ПО БПКПОЛН.
10. ВИЗНАЧЕННЯ НЕОБХІДНОГО СТУПЕНЯ ОЧИЩЕННЯ ПО ЗВАЖЕНИХ РЕЧОВИНАХ.
11. ВИЗНАЧЕННЯ НЕОБХІДНОГО СТУПЕНЯ ОЧИЩЕННЯ.
12. ВИЗНАЧЕННЯ СТУПЕНЯ УРАЖЕНОСТI ЛРС КОМIРНИМИ ШКIДНИКАМИ.

Переглядів: 1089