
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Імпульсна характеристика лінійної стаціонарної системи
Вступ
Системи, які застосовуються для обробки, перетворення та передачі сигналів, досить різноманітні по принципах внутрішнього пристрою та зовнішніх характеристик. Для того щоб їх можна було порівнювати та класифікувати, сформулюємо вихідні поняття.
Радіотехнічна система – сукупність фізичних об'єктів, між якими існують певні взаємодії. Безвідносно до призначення та рівня складності система завжди має вхід, на який подається зовнішній вхідний сигнал, у загальному випадку багатомірний, і вихід, з якого знімається перетворений вихідний сигнал. Якщо цікавляться лише зв'язком між сигналами на вході та виході і не описують внутрішні процеси в системі, то кажуть, що система являє собою «чорний ящик».
Формально система являє собою системний оператор (алгоритм) перетворення вхідного сигналу 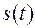 – впливуабо збудження, та сигнал на виході системи
– впливуабо збудження, та сигнал на виході системи 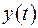 – відгукабо вихідна реакція системи. Символічне позначення операції перетворення (трансформації сигналу):
– відгукабо вихідна реакція системи. Символічне позначення операції перетворення (трансформації сигналу): 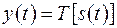 .
.
Системні оператори.Унайбільш простому випадку, як вхідний сигнал 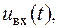 так і вихідний сигнал
так і вихідний сигнал 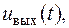 описуються одиночними функціями часу. У більш загальному випадку вхідний сигнал представляється у вигляді
описуються одиночними функціями часу. У більш загальному випадку вхідний сигнал представляється у вигляді 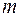 - мірного вектора
- мірного вектора

|
а вихідний сигнал - у вигляді n-мірного вектора
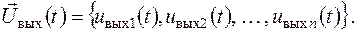
|
Закон зв'язку між сигналами 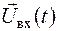 та
та 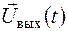 задають системним оператором Т, результатом впливу, якого на сигнал
задають системним оператором Т, результатом впливу, якого на сигнал 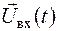 служить сигнал
служить сигнал 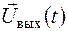 :
:
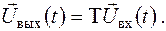
| (2.1) |
Системний операторT– це набір правил перетворення (transformation) сигналу 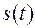 в сигнал
в сигнал 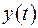 . Так, наприклад, у самому найпростішому випадку таким правилом може бути таблиця перекодування вхідних сигналів у вихідні.
. Так, наприклад, у самому найпростішому випадку таким правилом може бути таблиця перекодування вхідних сигналів у вихідні.
Для детермінованих вхідних сигналів співвідношення між вихідними та вхідними сигналами завжди однозначно задається системним оператором. У випадку надходження на вході системи випадкового вхідного процесу в ній відбуваються зміни статистичних характеристик сигналу (математичного очікування, дисперсії, кореляційній функції та ін.), які також визначаються системним оператором.
Щоб повністю задати систему, крім оператора системи варто вказати або визначити область 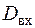 деякого функціонального простору, що називається областю допустимих вхідних впливів. Завдання цієї області описує характер вхідних сигналів, які можуть бути безперервними або дискретними, детермінованими або випадковими. Подібним же чином повинна бути зазначена область
деякого функціонального простору, що називається областю допустимих вхідних впливів. Завдання цієї області описує характер вхідних сигналів, які можуть бути безперервними або дискретними, детермінованими або випадковими. Подібним же чином повинна бути зазначена область 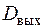 допустимих вихідних сигналів.
допустимих вихідних сигналів.
Математичною моделлю системиназивають сукупність системного оператора 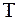 та двох областей допустимих сигналів
та двох областей допустимих сигналів 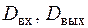 .
.
Класифікацію систем проводять на підставі істотних властивостей їх математичних моделей.
Стаціонарні та нестаціонарні системи. Система вважається стаціонарною та має постійні параметри, якщо її властивості (математичний алгоритм оператора перетворення) у межах заданої точності не змінюються ні в часі, ні від яких-небудь інших зовнішніх факторів. У противному випадку система є нестаціонарною, та називається параметричною або системою зі змінними параметрами. Серед останніх велике значення мають так звані адаптивні системи обробки даних. У цих системах відбувається, наприклад, оцінювання певних параметрів вхідних та вихідних сигналів, за результатами, порівняння яких здійснюється підстроювання параметрів перетворення (перехідної характеристики системи) таким чином, щоб забезпечити оптимальні по продуктивності умови обробки сигналів або мінімізувати похибку обробки.
Прийнято казати, що система стаціонарна, якщо її вихідна реакція не залежить від того, у який момент часу надходить вхідний сигнал. Якщо Т - оператор стаціонарної системи, то з рівності (2.1) слідує, що
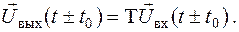
| (2.2) |
при будь-якому значенні 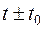 . Стаціонарні системи називають також системами з постійними в часі параметрами. Якщо ж властивості системи не інваріантні щодо вибору початку відліку часу, то таку систему називають нестаціонарною (системою зі змінними в часі параметрами або параметричною системою).
. Стаціонарні системи називають також системами з постійними в часі параметрами. Якщо ж властивості системи не інваріантні щодо вибору початку відліку часу, то таку систему називають нестаціонарною (системою зі змінними в часі параметрами або параметричною системою).
Теоретичне вивчення нестаціонарних систем, як правило, представляє набагато більш складну задачу, чим дослідження стаціонарних систем
Обидва зазначених класи систем широко застосовуються в радіотехніці, та будуть вивчатися в даному курсі.
Лінійні та нелінійні системи. Найважливіший принцип класифікації систем заснований на тому, що різні системи по-різному поводяться при подачі на вхід суми декількох сигналів. Якщо оператор системи такий, що справедливі рівності
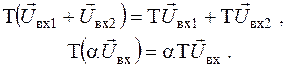
| (2.3) |
де 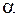 – довільне число, то дана система називається лінійною. Умови (2.3) виражають фундаментальні принципи суперпозиції та пропорційної подоби.
– довільне число, то дана система називається лінійною. Умови (2.3) виражають фундаментальні принципи суперпозиції та пропорційної подоби.
Якщо ці умови не виконуються, то кажуть, що система є нелінійною.
Строго кажучи, всі фізичні системи, з якими має справа радіотехніка, у тому або іншому ступені нелінійні. Однак існує багато систем, які досить точно описуються лінійними моделями. Так, практично завжди можна знехтувати не лінійністю звичайних резисторів, конденсаторів та деяких індуктивних елементів.
Нелінійні радіотехнічні пристрої містять у собі звичайно такі елементи, як напівпровідникові діоди та транзистори, що мають вольт-амперні характеристики складного виду.
Теорія нелінійних систем виявляється, як правило, досить складною. Далеко не всі результати можуть бути отримані тут аналітичним шляхом. Однак саме за допомогою нелінійних елементів здійснюються найважливіші перетворення радіотехнічних сигналів. Методи аналізу та розрахунку деяких нелінійних радіотехнічних пристроїв розглянуті в п. 2.4.
Лінійні та нелінійні системи становлять два основних класи систем обробки сигналів.
Термін лінійності (linear) означає, що система перетворення сигналів повинна мати довільну, але в обов'язковому порядку лінійний зв'язок між вхідним сигналом (збудженням) і вихідним сигналом (відгуком). У нелінійних (nonlinear) системах зв'язок між вхідним та вихідним сигналом визначається довільним нелінійним законом з доповненням частотного складу вхідного сигналу частотними складовими, які відсутні у вхідному сигналі.
Система вважається лінійною, якщо її реакція на вхідні сигнали адитивна (виконується принцип суперпозиції сигналів) і однорідна (виконується принцип пропорційної подоби). Інакше кажучи, відгук лінійної системи на зважену суму вхідних сигналів повинен дорівнювати зваженій сумі відгуків на окремі вхідні сигнали незалежно від їхньої кількості та для будь-яких вагових коефіцієнтів, у тому числі комплексних.
При програмній реалізації лінійних систем на ЕОМ особливих труднощів із забезпеченням лінійності в розумних межах значень вхідних і вихідних сигналів, як правило, не виникає. При фізичній (апаратній) реалізації систем обробки даних діапазон вхідних та вихідних сигналів, у якому забезпечується лінійність перетворення сигналів, завжди обмежений та повинен бути спеціально зазначений.
Зосереджені та розподілені системи. Інший критерій класифікації радіотехнічних систем заснований на порівнянні фізичних розмірів системи та робочої довжини хвилі. Якщо характерний розмір системи (наприклад, найбільша довжина з’єднаних провідників кола) виявляється набагато менше довжини хвилі, то виходить зосереджена система.
У зосередженому електричному колі завжди можна виділити фізичні області з переважною локалізацією енергії електричного поля (конденсатори) та магнітного поля (індуктивні елементи). Властивості зосереджених кіл слабко залежать від конфігурації з’єднаних провідників, тому для опису таких кіл прийнято використовувати їх абстрактні моделі, які мають назву принципові схеми.
У радіотехніці зосереджені системи широко застосовують аж до робочих частот у кілька сотень мегагерц. Аналіз та розрахунок зосереджених радіотехнічних систем проводять за допомогою законів Кірхгофа.
На частотах у кілька тисяч мегагерц, у так званому надвисокочастотному (НВЧ) діапазоні, фізичні розміри більшості пристроїв виявляються порівнянними з довжиною хвилі переданих коливань, так що стає необхідним врахування кінцевого часу поширення сигналу. Звичайні електричні кола у такому високочастотному діапазоні вже не можуть використовуватися та на зміну їм приходять системи з розподіленими параметрами (розподілені або хвильові системи). Так, замість з’єднаних провідників застосовуються відрізки металевих труб - хвилеводи, замість коливальних LC-контурів - їх розподілені аналоги, так називані об'ємними резонаторами. Теорія, методи аналізу та проектування розподілених систем досить складні і становлять зміст окремих радіотехнічних дисциплін.
Закінчивши короткий огляд принципів класифікації систем, сконцентруємо увагу на найпростішому їх виді - лінійних стаціонарних системах із зосередженими параметрами.
Основні системні операції. До базових лінійних операцій, з яких можуть бути сформовані будь-які лінійні оператори перетворення, є операції:
скалярного множення, 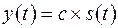 ,
,
зсуву 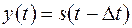 та
та
додавання сигналів 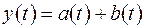 .
.
Для нелінійних систем виділимо важливий тип безінерційних операцій нелінійної трансформації сигналу, результати якої залежать тільки від його вхідних значень. До них відносяться, наприклад, операції обчислення квадрата, модуля та логарифмування сигналу:
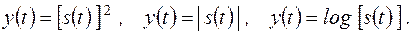
|
Інваріантність систем до зсуву. Система називається інваріантною до зсуву, якщо зсув вхідного сигналу по аргументах (часу, координатам простору й т.п.) викликає відповідний зсув вихідного сигналу:
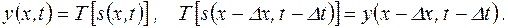
|
Це означає, що форма вихідного сигналу залежить тільки від вхідного сигналу, і не залежить від часу надходження сигналу на вхід системи. Інваріантність системи до зсуву є одним з підтверджень сталості її параметрів.
Лінійність та інваріантність до зсуву є незалежними властивостями систем і не визначають один одного. Так, наприклад, операція обчислення квадрату сигналу інваріантна до зсуву, але нелінійна.
У теорії аналізу та обробки даних основне місце займають системи, лінійні та інваріантні до зсуву ( ЛІС-системи). Вони мають досить широкі практичні можливості при відносній простоті математичного апарата. Надалі, якщо це спеціально не обмовляється, будемо мати на увазі саме такі системи.
Перевага, що віддається ЛІС-системам у методах обробки інформації, базується на можливості розкладання вхідного сигналу кожної, як завгодно складної форми, на складові найпростіших форм, відгук системи на які відомий і добре вивчений, з наступним обчисленням вихідного сигналу у вигляді суми відгуків на всі складові вхідного сигналу. Як найпростіші форми розкладання сигналів використовуються, як правило, одиничні імпульси та гармонічні складові. Розкладання по одиничних імпульсах застосовується при динамічному представленні сигналу залежно від реальних фізичних аргументів (часу, координат та ін.) та використовується операція згортки. Розкладання на гармонічні складові використовується при спектральному (частотному) представленні сигналу та перетворенні Фур'є.
З'єднання ЛІС-систем.При послідовному (каскадному) з'єднанні систем вихідний сигнал однієї системи служить вхідним сигналом для другої й т.д. залежно від кількості складових систем каскаду. Стосовно загальної системної операції перетворення порядок з'єднання вхідних елементів системи значення не має. Так, для двох послідовно з'єднаних систем на рис. 2.4:
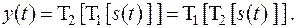
При паралельному з'єднанні вхідний сигнал надходить одночасно на входи всіх складових систем, а вихідні сигнали систем підсумуються:
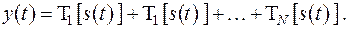
Утворені в результаті з'єднань система в цілому також є ЛІС-системою, якщо лінійні та інваріантні до зсуву елементи даної системи.
Чудова особливість лінійних систем - справедливість принципу суперпозиції - відкриває прямий шлях до систематичного рішення задач про проходження різноманітних сигналів через такі системи. У теорії сигналів є можливість представляти їх у вигляді сум елементарних імпульсів (спосіб динамічного представлення). Якщо вдасться тому або іншому способу знайти реакцію на виході, що виникає під впливом елементарного імпульсу на вході, то остаточним етапом рішення задачі буде підсумовування таких реакцій.
Намічений шлях аналізу заснований на часовому поданні властивостей сигналів та систем. Рівною мірою застосуємо, а часом і набагато більше зручний аналіз у частотній області, коли сигнали задаються рядами або інтегралами Фур'є. Властивості систем при цьому описуються їхніми частотними характеристиками, які вказують закон перетворення елементарних гармонійних сигналів.
Тестові сигнали (test signal). В якості тестових сигналів, які застосовуються при моделюванні та дослідженні систем обробки даних, звичайно використовуються сигнали найпростішого типу: гармонійні сінус-косинусні функції, дельта-функція та функція одиничного стрибка.
Дельта-функція або функція Дірака (рис.2.5). По визначенню, дельта-функція описується наступними математичними виразами (у сукупності):
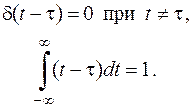
| (2.4) |
Функція 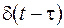 не є диференцируємою, і має розмірність, зворотну розмірності її аргументу, що безпосередньо слідує з без розмірності результату інтегрування. Значення дельта-функції дорівнює нулю скрізь за винятком точки
не є диференцируємою, і має розмірність, зворотну розмірності її аргументу, що безпосередньо слідує з без розмірності результату інтегрування. Значення дельта-функції дорівнює нулю скрізь за винятком точки 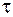 , де вона являє собою нескінченно вузький імпульс із нескінченно великою амплітудою, при цьому площа імпульсу дорівнює 1.
, де вона являє собою нескінченно вузький імпульс із нескінченно великою амплітудою, при цьому площа імпульсу дорівнює 1.
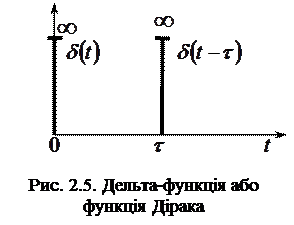 Дельта-функція є зручною математичною абстракцією. На практиці такі функції не можуть бути реалізовані з абсолютною точністю, тому що неможливо реалізувати значення, рівне нескінченності, у точці
Дельта-функція є зручною математичною абстракцією. На практиці такі функції не можуть бути реалізовані з абсолютною точністю, тому що неможливо реалізувати значення, рівне нескінченності, у точці 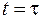 на аналоговій часовій шкалі, тобто певної за часом також з нескінченною точністю. Але у всіх випадках, коли площа імпульсу дорівнює 1, тривалість імпульсу досить мала, а за час його дії на вході якої-небудь системи сигнал на її виході практично не змінюється (реакція системи на імпульс значно перевищує тривалість самого імпульсу), вхідний сигнал можна вважати одиничною імпульсною функцією із властивостями дельта-функції.
на аналоговій часовій шкалі, тобто певної за часом також з нескінченною точністю. Але у всіх випадках, коли площа імпульсу дорівнює 1, тривалість імпульсу досить мала, а за час його дії на вході якої-небудь системи сигнал на її виході практично не змінюється (реакція системи на імпульс значно перевищує тривалість самого імпульсу), вхідний сигнал можна вважати одиничною імпульсною функцією із властивостями дельта-функції.
При всій своїй абстрактності дельта-функція має цілком певний фізичний зміст. Уявимо собі імпульсний сигнал прямокутної форми 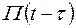 тривалістю q, амплітуда якого дорівнює 1/q, а площа відповідно дорівнює 1. При зменшенні значення тривалості q імпульс, скорочуючись по тривалості, зберігає свою площу, рівну 1, і зростає по амплітуді. Межа такої операції при
тривалістю q, амплітуда якого дорівнює 1/q, а площа відповідно дорівнює 1. При зменшенні значення тривалості q імпульс, скорочуючись по тривалості, зберігає свою площу, рівну 1, і зростає по амплітуді. Межа такої операції при 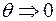 і має назву дельта-імпульса. Цей сигнал
і має назву дельта-імпульса. Цей сигнал  зосереджений в одній координатній точці
зосереджений в одній координатній точці 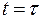 , конкретне амплітудне значення сигналу не визначене, але площа (інтеграл) залишається рівною 1. Це не миттєве значення функції в точці
, конкретне амплітудне значення сигналу не визначене, але площа (інтеграл) залишається рівною 1. Це не миттєве значення функції в точці 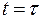 , а саме імпульс (імпульс сили в механіці, імпульс струму в електротехніці та т.п.) – математична модель короткої дії, значення якого дорівнює 1.
, а саме імпульс (імпульс сили в механіці, імпульс струму в електротехніці та т.п.) – математична модель короткої дії, значення якого дорівнює 1.
Дельта-функція має фільтруючу властивість. Суть його полягає в тому, що якщо дельта-функція 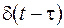 входить під інтеграл якої-небудь функції як множник, то результат інтегрування дорівнює значенню підінтегральної функції в точці t, де розташовується дельта-імпульс, тобто:
входить під інтеграл якої-небудь функції як множник, то результат інтегрування дорівнює значенню підінтегральної функції в точці t, де розташовується дельта-імпульс, тобто:
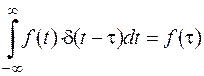 . .
| (2.5) |
Інтегрування в цьому виразі може обмежуватися найближчими околицями точки 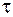 .
.
Функція одиничного стрибка або функція Хевісайда іноді називається також функцією включення (рис.2.6). Математичний вираз функції:
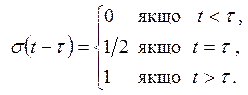
| (2.6) |
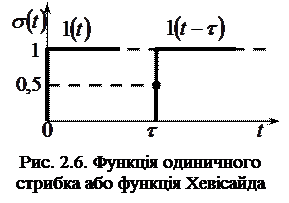 Іноді, функцію одиничного стрибка позначають як
Іноді, функцію одиничного стрибка позначають як 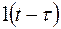 .
.
При моделюванні сигналів і систем значення функції стрибка в точці 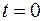 дуже часто приймають рівним 1, якщо це не має принципового значення.
дуже часто приймають рівним 1, якщо це не має принципового значення.
Функція одиничного стрибка використовується при створенні математичних моделей сигналів кінцевої тривалості. При множенні будь-якої довільної функції, у тому числі періодичної, на прямокутний імпульс, сформований із двох послідовних функцій одиничного стрибка
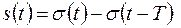 , ,
|
з її вирізається ділянка на інтервалі 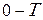 , та обнуляються значення функції за межами цього інтервалу.
, та обнуляються значення функції за межами цього інтервалу.
Функція одиничного стрибка пов'язана з 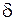 -функцією
-функцією
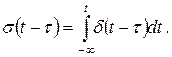
|
Функція Кронекера. Для дискретних та цифрових систем розрізнювальна здатність по аргументу сигналу визначається інтервалом його дискретизації 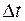 . Це дозволяє як одиничний імпульс використовувати дискретний інтегральний аналог дельта-функції – функцію одиничного відліку
. Це дозволяє як одиничний імпульс використовувати дискретний інтегральний аналог дельта-функції – функцію одиничного відліку 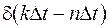 , що дорівнює 1 у координатній точці
, що дорівнює 1 у координатній точці 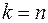 , і нулю у всіх інших точках. Функція
, і нулю у всіх інших точках. Функція 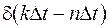 може бути визначена для будь-яких значень
може бути визначена для будь-яких значень 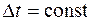 , але тільки для цілих значень координат
, але тільки для цілих значень координат 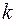 і
і 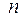 , оскільки інших номерів відліків у дискретних функціях не існує.
, оскільки інших номерів відліків у дискретних функціях не існує.
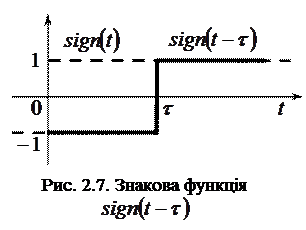 При описі сигналів часто використовується знакова функція (перемикаюча функція) – функція
При описі сигналів часто використовується знакова функція (перемикаюча функція) – функція 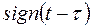 , що відповідає умові (рис. 2.7):
, що відповідає умові (рис. 2.7):
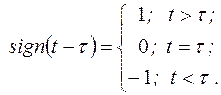
У математиці імпульсну характеристику називають функцією Гріна розглянутого оператора.
Намічений шлях аналізу заснований на часовому представленні властивостей сигналів та систем. Нехай деяка лінійна стаціонарна система описується оператором 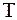 . Для простоти будемо вважати, що вхідний та вихідний сигнали одномірно. По визначенню, імпульсною характеристикою системи називається функція
. Для простоти будемо вважати, що вхідний та вихідний сигнали одномірно. По визначенню, імпульсною характеристикою системи називається функція 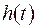 , що є відгуком системи на вхідний сигнал
, що є відгуком системи на вхідний сигнал 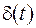 . Це означає, що функція
. Це означає, що функція 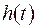 задовольняє рівнянню
задовольняє рівнянню
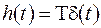 . .
| (2.7) |
Оскільки система стаціонарна, аналогічне рівняння буде й у випадку, якщо вхідний вплив зміщений у часі на довільну величину 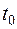 :
:
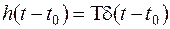 . .
| (2.8) |
Варто ясно уявити собі, що імпульсна характеристика, так само як і її породжена дельта-функція, є результатом розумної ідеалізації. З фізичної точки зору імпульсна характеристика приблизно відображає реакцію системи на вхідний імпульсний сигнал довільної форми з одиничною площею за умови, що тривалість цього сигналу достатньо мала в порівнянні з характерним часовим масштабом системи, наприклад періодом її власних коливань.
Інтеграл Дюамеля.Знаючи імпульсну характеристику лінійної стаціонарної системи, можна формально вирішити будь-яке завдання про проходження детермінованого сигналу через таку систему. Дійсно, у п. 1.2 було показано, що вхідний сигнал завжди допускає представлення виду
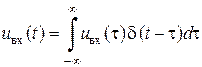 . .
|
Вихідна реакція, що відповідає йому
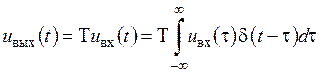 . .
| (2.9) |
Тепер візьмемо до уваги, що інтеграл є граничне значення суми, тому лінійний оператор 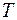 на підставі принципу суперпозиції може бути внесений під знак інтеграла. Далі, оператор
на підставі принципу суперпозиції може бути внесений під знак інтеграла. Далі, оператор 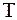 «діє» лише на величини, що залежать від поточного часу
«діє» лише на величини, що залежать від поточного часу 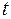 , але не від змінної інтегрування
, але не від змінної інтегрування 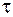 . Тому з виразу (2.9) слідує, що
. Тому з виразу (2.9) слідує, що
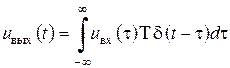 . .
|
Миттєве значення вихідного сигналу є функціоналом від вхідного сигналу. Тому імпульсну характеристику варто розглядати, строго кажучи, як узагальнену функцію (див. п. 1.2)або остаточно
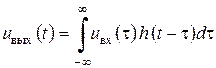 . .
| (2.10) |
Ця формула, що має фундаментальне значення в теорії лінійних систем, називається інтегралом Дюамеля. Співвідношення (2.10) свідчить про те, що вихідний сигнал лінійної стаціонарної системи являє собою згортку двох функцій - вхідного сигналу та імпульсної характеристики системи. Очевидно, формула (2.10) може бути записана також у вигляді
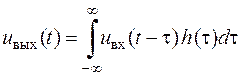 . .
| (2.11) |
 Отже, якщо імпульсна характеристика
Отже, якщо імпульсна характеристика 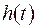 відома, то подальші етапи рішення зводяться до повністю формалізованих операцій.
відома, то подальші етапи рішення зводяться до повністю формалізованих операцій.
Якщо інтеграли (2.10) і (2.11) не вдається знайти аналітично, завжди можливий чисельний аналіз за допомогою ЕОМ
Приклад 2.4.Деяка лінійна стаціонарна система, внутрішній пристрій якої несуттєвий, має імпульсну характеристику, що представляє собою прямокутний відеоімпульс тривалістю 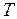 (рис.2.8). Імпульс виникає при
(рис.2.8). Імпульс виникає при 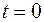 та має амплітуду
та має амплітуду 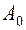 .
.
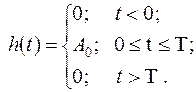
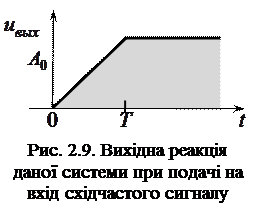
Визначити вихідну реакцію даної системи при подачі на вхід східчастого сигналу 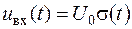 .
.
Застосовуючи формулу інтеграла Дюамеля (2.10), варто звернути увагу на те, що вихідний сигнал буде виглядати по-різному залежно від того, перевищує чи ні поточне значення 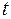 тривалість імпульсної характеристики. При
тривалість імпульсної характеристики. При 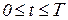 маємо
маємо
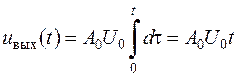 . .
|
 Якщо ж
Якщо ж 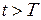 , то при
, то при 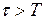 функція
функція 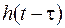 прямує в нуль, тому
прямує в нуль, тому 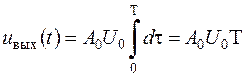 .
.
Знайдена вихідна реакція відображається кусочно-лінійним графіком (рис. 2.9).
Узагальнення на багатомірний випадок.Дотепер передбачалося, що як вхідний, так і вихідний сигнали одномірні. У більш загальному випадку системи із 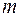 входами й
входами й 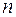 виходами варто ввести парціальні імпульсні характеристики
виходами варто ввести парціальні імпульсні характеристики 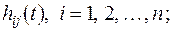
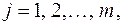 кожна з яких відображає сигнал на
кожна з яких відображає сигнал на 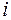 -м виході при подачі на
-м виході при подачі на 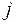 -й вхід дельта-функції. Сукупність функцій утворить матрицю імпульсних характеристик
-й вхід дельта-функції. Сукупність функцій утворить матрицю імпульсних характеристик
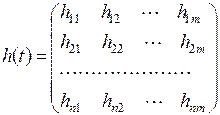 . .
| (2.12) |
Формула інтеграла Дюамеля в багатомірному випадку здобуває вид
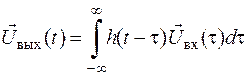 . .
| (2.13) |
де 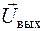 – n-мірний вектор;
– n-мірний вектор; 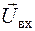 – m-мірний вектор.
– m-мірний вектор.
Умова фізичної реалізуємості.Який би не був конкретний вид імпульсної характеристики фізично здійсненної системи, завжди повинен виконуватися найважливіший принцип: вихідний сигнал, що відповідає імпульсному вхідному впливу, не може виникнути до моменту появи імпульсу на вході.
Звідси випливає дуже просте обмеження на вид припустимих імпульсних характеристик:
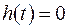 при при 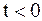 . .
| (2.14) |
Такій умові задовольняє, наприклад, імпульсна характеристика системи, яка розглянута в прикладі 2.4.
Легко бачити, що для фізично реалізованої системи верхня межа у формулі інтеграла Дюамеля може бути замінена на поточне значення часу:
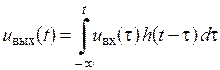 . .
| (2.15) |
Формула (2.15) має ясний фізичний зміст: лінійна стаціонарна система, виконуючи обробку сигналу, який надходить на вхід, проводить операцію зваженого підсумовування всіх його миттєвих значень, що існували «у минулому» при  . Роль вагової функції виконує при цьому імпульсна характеристика системи. Принципово важливо, що фізично реалізована система, ні за яких умов не здатна оперувати «майбутніми» значеннями вхідного сигналу.
. Роль вагової функції виконує при цьому імпульсна характеристика системи. Принципово важливо, що фізично реалізована система, ні за яких умов не здатна оперувати «майбутніми» значеннями вхідного сигналу.
Фізично реалізована система повинна бути, крім того, стійкою. Це означає, що її імпульсна характеристика повинна задовольняти умові абсолютної інтегруємості (рис.2.10)
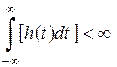 . .
| (2.16) |
Читайте також:
- I. Загальна характеристика політичної та правової думки античної Греції.
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
- II. ВИРОБНИЧА ХАРАКТЕРИСТИКА ПРОФЕСІЇ
- II. Морфофункціональна характеристика відділів головного мозку
- IV. Розподіл нервової системи
- IV. Система зв’язків всередині центральної нервової системи
- IV. Філогенез кровоносної системи
- POS-системи
- VI. Філогенез нервової системи
- Аварії на хімічно-небезпечних об’єктах та характеристика зон хімічного зараження.
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Перехідна характеристика лінійної стаціонарної системи |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |