• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Математичний опис динамічної системи

Вступ

Лінійними динамічними системами прийнято називати пристрої, які характеризуються наступною властивістю: їх вихідний сигнал визначається не тільки величиною вхідного сигналу в розглядаємий момент часу, але й «передісторією» цього сигналу. Інакше кажучи, динамічна система має деяку кінцеву або нескінченну «пам'ять», від характеру якої залежать особливості перетворення вхідного сигналу.

Серед різноманітних динамічних систем велике значення для теоретичної радіотехніки мають ті, які описуються диференціальними операторами. У загальному випадку мова йде про системи, для яких зв'язок між одномірними вхідним та вихідним сигналами встановлюється за допомогою наступного диференціального рівняння:

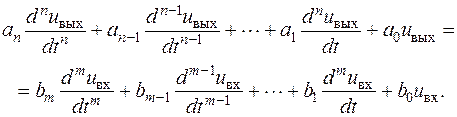
(2.32)

Саме такий виявляється динамічний зв'язок між миттєвими значеннями вхідного та вихідного сигналів в електричному колі із зосередженими параметрами. Якщо коло лінійне та стаціонарне, то всі коефіцієнти 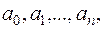та 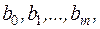– постійні дійсні числа.

Припустимо, що вхідний сигнал 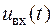заданий. Тоді права частина рівняння (2.32), яку можна умовно позначити , є відомою функцією. Аналіз поводження системи зводиться при цьому до добре вивченій в математиці проблемі рішення лінійного диференціального рівняння n-го порядку з постійними коефіцієнтами:

(2.33)

Порядок цього рівняння прийнято називати порядком динамічної системи.

Розглянемо кілька прикладів динамічних систем і відповідних їм диференціальних рівнянь.

Приклад 2.6. Дане RC-коло виду 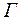- подібного чотириполюсника, яке збуджується джерелом ЕРС 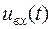. Вихідним сигналом служить напруга на конденсаторі (рис.2.14).

(2.34)

Оскільки струм у колі 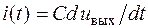, використовуючи другий закон Кірхгофа, одержуємо диференціальне рівняння RC-кола, яке є

системою першого порядку, та має назву інерційного елемента.

Отже, RC - коло є прикладом динамічної системи 1-го порядку. Найважливіший параметр цього кола – постійна часу , що визначає характерний часовий масштаб протікання процесів у системі.

Приклад 2.7. Дана більш складна система (рис.2.15), яка утворена двома - колами, які розділені ідеальним підсилювачем з коефіцієнтом підсилення 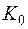. Вхідний опір підсилювача необмежено великий, а вихідний опір нескінченно малий, тому посилювач є ідеальним елементом розв'язки між колами.

Уводячи два постійні час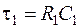и й 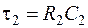за аналогією з попереднім прикладом маємо наступні диференціальні рівняння 1-го порядку:

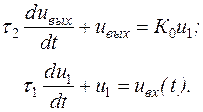
Виключивши звідси допоміжну величину 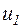одержуємо диференціальне рівняння кола:

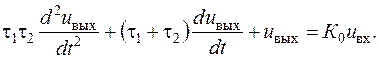
(2.35)

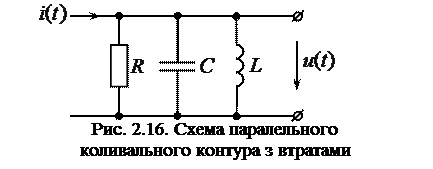
Розглянуте тут більш складне RC - коло виявляється вже системою 2-го порядку.

Приклад2.8. Знайти диференціальне рівняння паралельного коливального контуру із втратами (рис.2.16), враховуючи, що вхідним сигналом служить струм 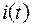, а вихідним сигналом є напруга 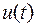на контурі.

Підсумовуючи струми

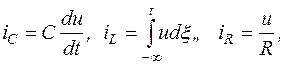
одержуємо рівняння

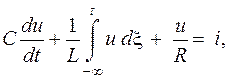
яке шляхом однократного диференціювання за часом приводиться до виду

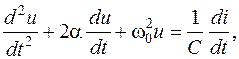
(2.36)

де 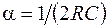– коефіцієнт загасання контуру, 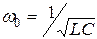частота власних коливань у контурі без втрат.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. VI. Філогенез нервової системи
9. Автокореляційна характеристика системи
10. АВТОМАТИЗОВАНІ СИСТЕМИ ДИСПЕТЧЕРСЬКОГО УПРАВЛІННЯ
11. АВТОМАТИЗОВАНІ СИСТЕМИ УПРАВЛІННЯ ДОРОЖНІМ РУХОМ
12. Автоматизовані форми та системи обліку.

Переглядів: 1505