• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Власні коливання динамічних систем

Щоб повністю визначити поводження динамічної системи, яка описується рівнянням (2.33), потрібно врахувати початкові умови, які характеризують внутрішній стан системи в деякий фіксований момент часу. Звичайно прийнято задавати шукану функцію і її 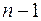похідну при :

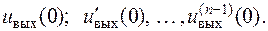
(2.36)

З теорії диференціальних рівнянь відомо [9], що рішенням рівняння (2.33), що задовольняє будь-яким початковим умовам, є сума деякого часткового рішення неоднорідного рівняння, у якого права частина відмінна від нуля, і загального рішення однорідного рівняння

(2.37)

Проблема рішення однорідного диференціального рівняння пов'язана зі знаходженням кореня характеристичного рівняння системи

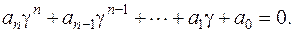
(2.38)

Дане рівняння має рівно коренів. Оскільки коефіцієнти рівняння дійсні, корені 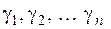можуть бути або дійсними, або комплексно-спряженими. Якщо всі корені різні, то загальне рішення однорідного рівняння (2.37), що описує власні коливання системи, має вигляд

(2.39)

де – постійні числа, які обумовлені початковими умовами.

Якщо ж деякі з коренів виявляються кратними, то складові загального рішення однорідного рівняння трохи ускладнюються за рахунок появи секулярних (вікових) множників. Так, якщо являє собою k-кратний корінь, то йому відповідає сукупність власних коливань виду

Розглянемо приклади власних коливань у лінійних стаціонарних колах.

Приклад 2.9. Аперіодична розрядка конденсатора ємністю , попередньо зарядженого до напруги та у момент часу, що замикається на резистор опором 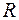(рис.2.17).

Коло описується наступним диференціальним рівнянням щодо змінної 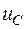– напруги на конденсаторі:

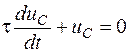
при єдиній початковій умові .

Характеристичне рівняння має корінь .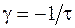

Звідси знаходимо загальне рішення рівняння вільних коливань:

.

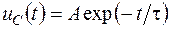Постійна часу .

Для того щоб задовольнити початковій умові, варто прийняти 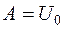. Остаточно маємо .

Отже, негативному дійсному кореню характеристичного рівняння відповідає власне коливання, яке експоненціально зменшується в часі.

Постійна часу 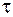даного кола є проміжок часу, протягом якого вільний процес загасає в 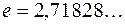раз (рис. 2.18).

Приклад2.10. Коливальна розрядка конденсатора (рис. 2.19). Нехай попередній приклад ускладнений тим, що в колі є також індуктивний елемент .

У контурі з індуктивним елементом струм не може змінитися стрибком. Диференціальне рівняння кола щодо струму , складене на підставі другого закону Кірхгофа, має вигляд

(2.40)

де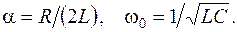

Перша початкова умова 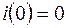обумовлена наявністю в контурі індуктивного елемента.

Напруга на резисторі в початковий момент часу дорівнює нулю в силу першої умови.

У початковий момент часу напруга на конденсаторі врівноважується ЕРС самоіндукції:

звідки треба друга початкова умова:

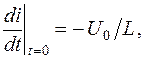
Характеристичне рівняння даного кола

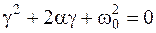
має комплексно-спряжений корінь

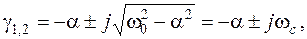
де – частота власних коливань системи. Якщо втрати в контурі досить малі, то , тому .

Загальне рішення однорідного рівняння

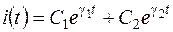
(2.41)

містить коефіцієнти та 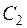, які задовольняють системі алгебраїчних рівнянь (див. початкові умови):

звідки

Підставивши ці коефіцієнти у вираз (2.41), одержимо остаточно (рис. 2.20)

2.42

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. II. Бреттон-Вудська система (створена в 1944 р.)
6. III етап. Системний підхід
7. IV. Розподіл нервової системи
8. IV. Система зв’язків всередині центральної нервової системи
9. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
10. IV. Філогенез кровоносної системи
11. OSI - Базова Еталонна модель взаємодії відкритих систем
12. POS-системи

Переглядів: 1048