• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Частотні характеристики лінійних стаціонарних систем

До них відносять частотний коефіцієнт передачі, що включає амплітудно-частотну та фазочастотну характеристики.

Частотний коефіцієнт передачі. При математичному дослідженні систем особливий інтерес представляють такі вхідні сигнали, які, будучи перетворені системою, залишаються незмінними за формою. Якщо є рівність

,

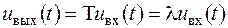(2.21)

то 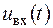є власною функцією системного оператора 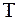, а число 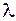, у загальному випадку комплексне,— його власним значенням.

Покажемо, що комплексний сигнал 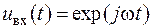при будь-якому значенні частоти 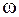є власна функція лінійного стаціонарного оператора. Для цього скористаємося інтегралом Дюамеля виду (2.11) і обчислимо

.

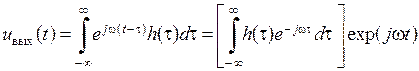(2.22)

Звідси видно, що власним значенням системного оператора є комплексне число:

.

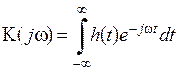(2.23)

називане частотним коефіцієнтом передачі системи. Формула (2.23) установлює принципово важливий факт – частотний коефіцієнт передачі й імпульсна характеристика лінійної стаціонарної системи зв'язані між собою перетворенням Фур'є. Тому завжди, знаючи функцію 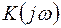можна визначити імпульсну характеристику

.

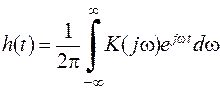(2.24)

Ми підійшли до найважливішого положення теорії лінійних стаціонарних систем - будь-яку таку систему можна розглядати або в часовій області за допомогою її імпульсної або перехідної характеристик, або в частотній області, задаючи частотний коефіцієнт передачі. Обидва підходи рівноцінні й вибір одного з них диктується зручностями одержання вихідних даних про систему й простоту обчислень.

На закінчення відзначимо, що частотні властивості лінійної системи, що має 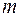входів і 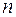виходів, можна описати матрицею частотних коефіцієнтів передачі

.

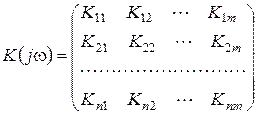(2.25)

Тут 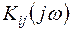– частотний коефіцієнт передачі між j-м входом і i-м виходом.

Між матрицям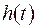и й 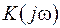існує закон зв'язку, аналогічний тому, що заданий формулами (2.23), (2.24).

Амплітудно-частотна та фазочастотна характеристики. Функція 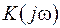має просту інтерпретацію: якщо на вхід системи надходить гармонічний сигнал з відомою частотою 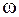й комплексною амплітудою 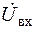, те комплексна амплітуда вихідного сигналу (рис. 2.11)

.

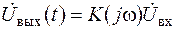(2.26)

Часто користуються представленням частотного коефіцієнта передачі в показовій формі:

.

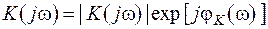(2.27)

Обидві вхідні сюди дійсні функції носять спеціальні назви: 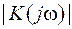– амплітудно-частотна характеристика (АЧХ), 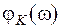– фазочастотна характеристика (ФЧХ) системи.

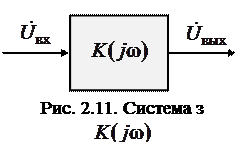Є прилади, що дозволяють експериментально вимірювати АЧХ і ФЧХ радіотехнічних пристроїв у всіляких діапазонах частот.

Обмеження, що накладаються на частотний коефіцієнт передачі. Далеко не кожна функція 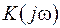може бути частотним коефіцієнтом передачі фізично реалізованої системи. Найпростіше обмеження пов'язане з тим, що імпульсна характеристика 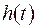такої системи зобов'язана бути дійсною. У силу властивостей перетворення Фур'є (див. п. 1.3) це означає, що

.

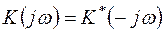(2.28)

Відповідно до формули (2.28) модуль частотного коефіцієнта передачі (АЧХ) є парна, а фазовий кут (ФЧХ) - непарна функція частоти.

Набагато складніше відповістити на запитання про те, яким повинен бути частотний коефіцієнт передачі для того, щоб виконувалися умови фізичної реалізуємості (2.14) і (2.16). Приведемо без доказу остаточний результат, відомий за назвою критерію Пелі-Вінера: частотний коефіцієнт передачі фізично реалізованої системи повинен бути таким, щоб існував інтеграл

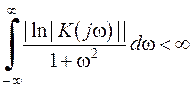– критерій Пелі-Вінера

(2.29)

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. II. Бреттон-Вудська система (створена в 1944 р.)
6. II. Критерій найбільших лінійних деформацій
7. III етап. Системний підхід
8. IV. Розподіл нервової системи
9. IV. Система зв’язків всередині центральної нервової системи
10. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
11. IV. Філогенез кровоносної системи
12. OSI - Базова Еталонна модель взаємодії відкритих систем

Переглядів: 1228