• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Стійкість динамічних систем

По визначенню, лінійна динамічна система називається стійкою, якщо всі її власні коливання загасають у часі. Необхідною й достатньою умовою стійкості системи є заперечність дійсних частин всіх коренів характеристичного рівняння (2.38).

Ці корені не повинні бути також і чисто уявними. Хоча при цьому власні коливання є гармонічні функції виду

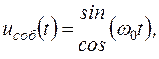
невеликі випадкові зміни параметрів системи можуть привести до переходу її в нестійкий режим, коли 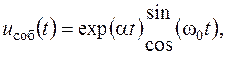являють собою експоненціальну наростаючі по амплітуді коливання (рис. 2.25).

Якщо порядок динамічної системи досить високий, то пряма перевірка стійкості, заснована на пошуку коренів характеристичного рівняння, може виявитися досить скрутною. Тому були розроблені спеціальні критерії стійкості, що дозволяють визначати наявність коренів із позитивними дійсними частинами безпосередньо по виду коефіцієнтів, минаючи саме рішення характеристичного рівняння.

Виникнення наростаючих власних коливань в електричних колах можливо лише тоді, коли в складі кола, крім пасивних елементів 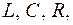містяться активні елементи, що передають у коло частину енергії від зовнішніх джерел. Розповсюдженою моделлю такого активного елемента служить резистор з негативним опором.

Розглянута система буде самовільно збуджуватися, якщо наявний в ній негативний опір

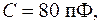
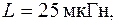
Приклад 2.14. Коливальний контур з параметрами 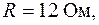містить резистор з негативним опором 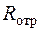, який включений паралельно індуктивному елементу (рис. 2.26). Визначити критичне значення цього опору, при якому виникає нестійкість кола.

Диференціальне рівняння даного кола, складене щодо напруги на індуктивному елементі, має вигляд

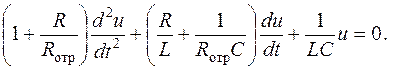
(2.46)

Корен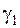і і 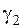характеристичного рівняння мають дійсні частини

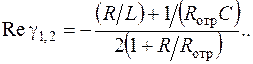
Система переходить у нестійкий режим, коли величина 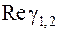обертається в нуль. Звідси знаходимо критичне значення негативного опору:

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. II. Бреттон-Вудська система (створена в 1944 р.)
6. III етап. Системний підхід
7. IV. Розподіл нервової системи
8. IV. Система зв’язків всередині центральної нервової системи
9. IV. УЗАГАЛЬНЕННЯ І СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО
10. IV. Філогенез кровоносної системи
11. OSI - Базова Еталонна модель взаємодії відкритих систем
12. POS-системи

Переглядів: 966