
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Необхідна та достатня умови
В ®`А – обернене до протилежного або протилежне до оберненого
А ®`В – протилежне твердження
В ® А – обернене твердження
А ® В – пряме твердження
Розглянемо кілька тверджень, що одержуються з простих тверджень А та В за допомогою операцій імплікації та заперечення.
Обернене та протилежне твердження
IV. Застосування математичної логіки
Твердженнями такої логічної форми ми багато раз користувались при вивченні математики. Виникає питання: які з цих тверджень між собою логічно еквівалентні? На жаль, тільки не велика кількість тих, хто почав вивчати математичну логіку, мають розвинену логічну інтуїцію і правильно відповідають на це питання. Більшість вважають, що логічно еквівалентні твердження 1-2, 1-3 або 2-4. Кілька хвилин достатньо, щоб скласти таблицю істинності і правильно відповісти на поставлене питання.
| А В | `А | `В | А ® В | В ®А | `А ®`В | `В ®`А |
| 0 0 0 1 1 0 1 1 |
Бачимо, що А ® В =`В ®`А та В ® А =`А ®`В тобто, логічно еквівалентні пряме твердження і обернене до протилежного та обернене і протилежне твердження. Як легко побачити, тут немає двох видів зв’язку між логічними формами, тут тільки один вид зв’язку, бо з першого твердження одержується четверте точно так же, як з другого одержується трете твердження.
Більшість логічних помилок при вивченні математики пов’язана з нерозумінням того, що перше і друге твердження (А ® В, В ® А ) не є логічно еквівалентними, їх не можна підміняти одне одним. Такі помилки не випадкові, бо логічний аналіз шкільного підручника геометрії [5] говорить про те, що цим питанням не приділено достатньо уваги.
Введемо позначення: D – достатня умова, Т – твердження, N – необхідна умова.
Означення. Достатньою умовою по відношенню до деякого твердження називають таку умову, з якої це твердження випливає.
Цьому означенню відповідає формула D®T
Означення. Необхідною умовою по відношенню до деякого твердження називають таку умову, яка з цього твердження випливає.
Цьому означенню відповідає формула T®N
Пригадуючи зв’язок між прямим твердженням та оберненим до протилежного маємо:

Саме в формі заперечення використовують практично означення необхідної умови, і в такій же формі воно зустрічається в математичній літературі.
Означення. Необхідною умовою по відношенню до деякого твердження називають таку умову, при невиконанні якої твердження не виконується)
Проаналізуємо форму теорем з необхідною і достатньою умовами.
Теорема. Для А необхідно і досить В.
В цій теоремі А є твердженням по відношенню до якого В є як необхідною, так і достатньою умовами. За означенням, з твердження випливає необхідна умова. Тому маємо:
Необхідність. А ® В.
За означенням достатньої умови, з достатньої умови випливає твердження. Тому маємо:
Достатність. В ® А.
В шкільній математиці поняття необхідної і достатньої умов використовуються так, що вони завжди виражаються одним і тим самим твердженням. Створюється помилкове враження, що необхідна умова завжди є достатньою і навпаки. Тому корисними є приклади в яких необхідна умова не є достатньою і достатня не є необхідною.
| Достатня умова | Твердження | Необхідна умова |
Сума цифр числа 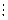 3
Число 3
Число 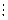 9
Число =15
Число = 10 × 10 -1 9
Число =15
Число = 10 × 10 -1
| Число 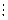 3
Число 3
Число 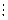 3
Число 3
Число 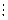 3
Число 3
Число 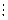 3 3
| Сума цифр числа 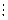 3
Число > 2
Число ≠ 7
Число не є простим 3
Число > 2
Число ≠ 7
Число не є простим
|
Тотожність (D ® T)(T ® N) ® (D ® N) º 1 (ДС) виражає те, що для фіксованого твердження з любої достатньої умови випливають всі необхідні умови.
Поняття необхідної і достатньої умови є відносними, вони визначаються по відношенню до деякого твердження. Якщо потрібно визначити яка умова використовується в змістовній формі, то спочатку знаходимо твердження, а потім визначаємо яка це умова. Наприклад, в теоремі А → В, якщо Т = А, то В = N, а якщо Т = В, то А = D.
DTN – ключ для пригадування означень D®T та T®N.
Читайте також:
- Аналогія як умовивід
- Блок 4. Умови та охорона праці.
- Блок перевірки умови
- БУДОВА ТА УМОВИ ФОРМУВАННЯ ШАРУВАТИХ ТОВЩ
- Види аудиторських висновків та умови їх надання
- Види і типи організаційних структур та умови їх ефективного застосування
- Види й типи організаційних структур та умови їх ефективного застосування
- Винесення внутрішніх, розумових дій назовні називають екстеріоризацією.
- Вирішення суперечок між суб'єктами страхування. Умови припинення дії договору.
- Відносно невисокий економічний потенціал Франції, пасивність буржуазії, зумовили відставання країни у завоюванні колоній та зовнішній торгівлі.
- Вплив ресурсних обмежень на умови розвитку міст
- Всебічний розвиток особистості людини як необхідна умова соціального розвитку персоналу організації
| <== попередня сторінка | | | наступна сторінка ==> |
| ІІІ. Бульова алгебра | | | Ознаки, властивості, означення |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |