
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ІІІ. Бульова алгебра
8. Означення бульової алгебри
Запишемо основні тотожності бульової алгебри.
1. x y=y
y=y x
x
2. x y=y
y=y x
x
3. x (y
(y z)=(x
z)=(x y)
y)  z
z
4. x (y
(y z)=(x
z)=(x y)
y)  z
z
5. x (y
(y z)=(x
z)=(x y)
y)  (x
(x z)
z)
6. x (y
(y z)=(x
z)=(x y)
y)  (x
(x z)
z)
7. 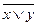 =
=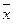

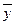
8. 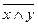 =
=

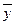
9. x x=x
x=x
10. x x=x
x=x
11. x 0=x
0=x
12. x 1=x
1=x
13. x
 =1
=1
14. x
 =0
=0
15. x 1=1
1=1
16. x 0=0
0=0
17. 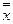 =x
=x
Тотожності 1 – 6 виражають комутативний (переставний), асоціативний (сполучний), дистрибутивний (розподільний) закони відповідно для диз’юнкції та кон’юнкції. Тотожності 7- 8 мають назву правил Де Моргана. Тотожністі 13 та 14 називають відповідно законами виключеного третього та суперечності. Звичайно, всі тотожності виконуються в алгебрі висловлень.
Означення. Бульовою алгеброю називають числення висловлень, в якому операції заперечення, кон’юнкція та диз’юнкція (¯ , 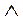 ,
, 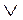 ) визначаються тотожностями 1 -- 17.
) визначаються тотожностями 1 -- 17.
9. Доведеня тотожностей в бульовій алгебрі
Якщо в алгебрі висловлень два основних питання (рівносильність і тотожня істинність) вирішуються таблицями істинності, то в бульовій алгебрі ці ж питання вирішуються за допомогою тотожних перетворень. Доведемо наступні дві тотожності:
18. x xy=x
xy=x
19. x(x y)=x
y)=x
Спочатку доведемо, що ці тотожності еквівалентні, тобто, якщо виконується одна з них, то інша теж виконується.
x xy =6 ( x
xy =6 ( x x )
x )  ( x
( x y )=9 x
y )=9 x ( x
( x y ).
y ).
Ми довели, що ліві частини обох тотожностей є рівносильні формули, з чого і випливає еквівалентність обох тотожностей. Тепер доведемо одну з цих тотожностей.
x xy =12 (x
xy =12 (x 1)
1)  (x
(x y)=5 x
y)=5 x (1
(1 y)=1 x
y)=1 x (y
(y 1)=15 x
1)=15 x 1=12 x.
1=12 x.
Як бачимо, дослідження формул за допомогою тотожних перетворень значно складніше, ніж за допомогою таблиць. Такими тотожними перетвореннями не можна дослідити нерівносильні формули. Тому в бульовій алгебрі вводять формули у досконалих формах, які відіграють таку ж роль, що й таблиці істинності алгебри висловлень.
10. Елементарні добутки
Починаємо вивчати формули у досконалих формах. Цих форм є дві:
Д Д Н Ф – досконала диз’юнктивна нормальна форма.
Д К Н Ф – досконала кон’юнктивна нормальна форма.
Означення. Елементарним добутком для n-місної бульової функції називають формулу, що являє собою логічний добуток n різних змінних, взятих із запереченням або без нього.
Наприклад: 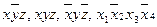 .
.
Розглянемо властивості елементарних добутків.
Властивість 1. Бульова функція, що виражається елементарним добутком, приймає значення 1 і тільки на одному наборі.
Випливає з означення елементарного добутку і означення кон’юнкції.
Приклади: 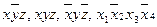 . Ці елементарні добутки приймають значення 1 відповідно на наборах 1 0 1, 1 1 1, 0 1 0, 1 0 1 0.
. Ці елементарні добутки приймають значення 1 відповідно на наборах 1 0 1, 1 1 1, 0 1 0, 1 0 1 0.
Властивість 2. Якщо бульова функція приймає значення 1 тільки на одному наборі, то її можна представити формулою у вигляді елементарного добутку.
Випливає з означення елементарного добутку і означення кон’юнкції.
11. Означення формули у ДДНФ. Перехід від таблиці до формули
ДДНФ – досконала диз’юнктивна нормальна форма.
Означення. Формулою у ДДНФ для n-місної бульової функції називають логічну суму різних n-місних елементарних добутків.
Приклади: 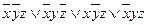 ,
, 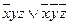 ,
, 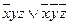

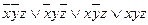 .
.
Властивість. Кожній одиниці з таблиці значень бульової функції відповідає елементарний добуток, який входить як логічний доданок у відповідну формулу в Д Д Н Ф.
Ця властивість випливає з 2-ої властивості елементарних добутків і означення логічної операції диз’юнкція.
З властивості формул у Д Д Н Ф випливає, що для того щоб записати формулою бульову функцію, яка задана таблицею, потрібно записати доданками стільки елементарних добутків, скільки є одиниць в таблиці значень бульової функції і проставити заперечення над тими змінними, проти яких у відповідних одиничних наборах стоять нулі.
Приклад. Бульові функції 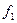 та
та  задані таблицями своїх значень. Побудувати для них формули у Д Д Н Ф.
задані таблицями своїх значень. Побудувати для них формули у Д Д Н Ф.
  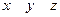 
| 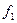
| 
| 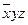
| 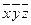
| 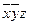
| 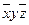
| 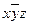
|
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |

Для кращого розуміння побудови формул, в таблиці наведені значення функцій для відповідних елементарних добутків.
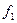 =
=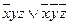 ,
,  =
=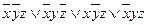 .
.
12. Теорема про представлення бульової функції формулою у ДДНФ
Теорема. Довільну бульову функцію, що не дорівнює тотожно нулю, можна представити формулою у Д Д Н Ф.
Доведення. Нехай бульова функція задана таблицею значень. В цій таблиці повинна бути хоч одна одиниця, бо тотожно хибна формула в Д Д Н Ф не представляється.
| x1 x2 ... xn-1 xn | 
| 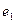
| 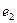
| 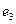
| ... | 
|
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 ....................... 1 1 1 0 1 1 1 1 | ... | ... | ... | ... | ... ... ... ... ... ... ... | ... |
Для функції  будуємо допоміжні функції
будуємо допоміжні функції 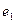 ,
, 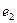 ,
, 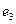 , ...,
, ...,  так, щоб кожній одиниці функції
так, щоб кожній одиниці функції  відповідала одна і тільки допоміжна функція
відповідала одна і тільки допоміжна функція  яка приймає значення 1 на тому ж наборі, що і функція
яка приймає значення 1 на тому ж наборі, що і функція  . Запишемо допоміжні функції формулами в формі елементарних добутків.
. Запишемо допоміжні функції формулами в формі елементарних добутків.
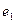 =
=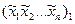 ,
, 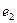 =
=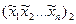 ,
, 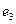 =
=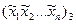 , ...,
, ...,  =
=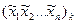 .
.
Хвилясті лінії над змінними означають, що заперечення може бути, а може і не бути. Ці формули допоміжних функцій відрізняються одна від одної розташуванням заперечень. Доведемо рівність  =
=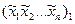

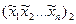

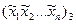
 ...
... 
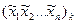 .
.
Доведення: 
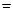
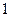
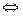
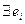
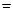
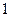
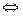
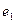

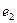
 ...
...
 =
=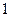 .
.
Наслідок. Представлення бульової функції формулою у Д Д Н Ф єдине з точністю до розташування логічних доданків і логічних співмножників в них.
Наслідок випливає з теореми і з того, що представлення бульової функції таблицею єдине.
13. Алгоритм зведення формули до ДДНФ
Алгоритм зведення формули до Д Д Н Ф полягає у виконанні тотожних перетворень за формулами наступних п’яти пунктів.
1. 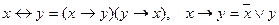
2. 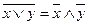 ,
, 
3. 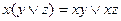
4. 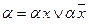 , де
, де 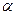 - добуток змінних без х
- добуток змінних без х
5. 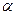

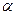 =
=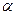 , де
, де 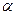 - елементарний n – місний добуток
- елементарний n – місний добуток
В разі потреби для спрощення формул використовують тотожності 1 - 17
Приклад. №34(4), стор. 15, [3]. Звести до Д Д Н Ф формулу 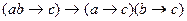 .
.
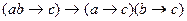 =1
=1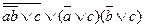 =2
=2 =3
=3
=3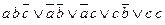 =4
=4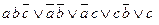 =5
=5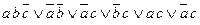 =6
=6
=6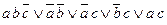 =7
=7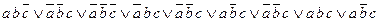 =8
=8
=8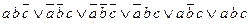 .
.
Пояснення.
1) Позбавляємось від імплікації, використовуючи тотожність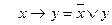 1-го пункту алгоритму.
1-го пункту алгоритму.
2) Використовуємо правило Де Моргана 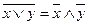 2-го пункту алгоритму.
2-го пункту алгоритму.
3) Використовуємо тотожність  з тотожностей 1 – 17 та тотожність
з тотожностей 1 – 17 та тотожність 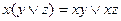 з 3–го пункту алгоритму.
з 3–го пункту алгоритму.
4) Використовуємо тотожність 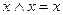 з тотожностей 1 – 17.
з тотожностей 1 – 17.
5) Використовуємо тотожність 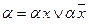 4–го пункту алгоритму.
4–го пункту алгоритму.
6) Використовуємо тотожність 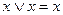 з тотожностей 1 – 17.
з тотожностей 1 – 17.
7) Використовуємо тотожність 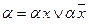 4–го пункту алгоритму.
4–го пункту алгоритму.
8) Використовуємо тотожність 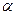

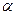 =
=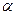 5–го пункту алгоритму.
5–го пункту алгоритму.
14. Елементарні суми
Означення. Елементарною сумою для n-місної бульової функції називають формулу, що являє собою логічний суму n різних змінних, взятих із запереченням або без нього.
Наприклад:  .
.
Розглянемо властивості елементарних сум.
Властивість 1. Бульова функція, що виражається елементарною сумою, приймає значення 0 і тільки на одному наборі.
Випливає з означення елементарного суми і означення диз’юнкції.
Приклади:  . Ці елементарні суми приймають значення 0 відповідно на наборах 0 1 0, 0 0 0, 1 0 1, 0 1 0 1.
. Ці елементарні суми приймають значення 0 відповідно на наборах 0 1 0, 0 0 0, 1 0 1, 0 1 0 1.
Властивість 2. Якщо бульова функція приймає значення 0 тільки на одному наборі, то її можна представити формулою у вигляді елементарноі суми.
Випливає з означення елементарного суми і означення диз’юнкції.
15. Означення формули у ДКНФ. Перехід від таблиці до формули
ДКНФ – досконала кон’юнктивна нормальна форма.
Означення. Формулою у ДКНФ для n-місної бульової функції називають логічний добуток різних n-місних елементарних сум.
Приклади:  ,
, 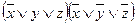 .
.
Властивість. Кожному нулю з таблиці значень бульової функції відповідає елементарна сума, яка входить як логічний множник у відповідну формулу в Д К Н Ф.
Ця властивість випливає з 2-ої властивості елементарних сум і означення логічної операції кон’юнкція.
З властивості формул у Д К Н Ф випливає, що для того щоб записати формулою бульову функцію, яка задана таблицею, потрібно записати множниками стільки елементарних сум, скільки є нулів в таблиці значень бульової функції і проставити заперечення над тими змінними, проти яких у відповідних нульових наборах стоять одиниці.
Приклад. Бульові функції 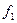 та
та  задані таблицями своїх значень. Побудувати для них формули у Д К Н Ф.
задані таблицями своїх значень. Побудувати для них формули у Д К Н Ф.
 
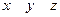 
|
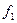
|

|
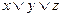
|
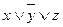
|

|
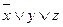
|
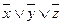
|
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |

Для кращого розуміння побудови формул, в таблиці наведені значення функцій для відповідних елементарних сум.
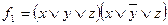 ,
, .
.
16. Теорема про представлення бульової функції формулою у ДКНФ
Теорема. Довільну бульову функцію, що не дорівнює тотожно одиниці, можна представити формулою у Д К Н Ф.
Доведення. Нехай бульова функція задана таблицею значень. В цій таблиці повинен бути хоч один нулик, бо тотожно істина формула в Д К Н Ф не представляється.
| x1 x2 ... xn-1 xn | 
| 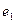
| 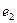
| 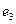
| ... | 
|
| 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 ....................... 1 1 1 0 1 1 1 1 | ... | ... | ... | ... | ... ... ... ... ... ... ... | ... |
Для функції  будуємо допоміжні функції
будуємо допоміжні функції 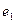 ,
, 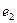 ,
, 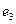 , ...,
, ...,  так, щоб кожному нулю функції
так, щоб кожному нулю функції  відповідала одна і тільки допоміжна функція
відповідала одна і тільки допоміжна функція  яка приймає значення 0 на тому ж наборі, що і функція
яка приймає значення 0 на тому ж наборі, що і функція  . Запишемо допоміжні функції формулами в формі елементарних сум.
. Запишемо допоміжні функції формулами в формі елементарних сум.
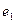 =
=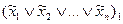 ,
, 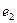 =
=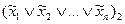 ,
, 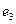 =
= , ...,
, ...,  =
=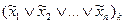 .
.
Хвилясті лінії над змінними означають, що заперечення може бути, а може і не бути. Ці формули допоміжних функцій відрізняються одна від одної розташуванням заперечень. Доведемо рівність
 =
=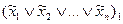
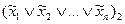
 ...
... 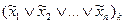 .
.
Доведення: 
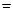 0
0 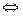
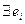
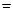 0
0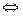
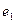
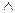
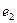
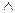 ...
...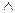
 = 0.
= 0.
Наслідок. Представлення бульової функції формулою у Д К Н Ф єдине з точністю до розташування логічних співмножників і логічних доданків в них.
Наслідок випливає з теореми і з того, що представлення бульової функції таблицею єдине.
17. Алгоритм зведення формули до ДКНФ
Алгоритм зведення формули до Д К Н Ф полягає у виконанні тотожних перетворень за формулами наступних п’яти пунктів.
1. 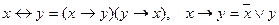
2. 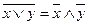 ,
, 
3. 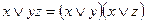
4. 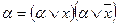 , де
, де 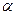 - логічна сума змінних без х
- логічна сума змінних без х
5. 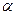
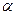 =
=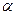 , де
, де 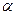 - елементарна n – місна сума
- елементарна n – місна сума
В разі потреби для спрощення формул використовують тотожності 1 - 17
Приклад. №34(4), стор. 15, [3]. Звести до Д К Н Ф формулу 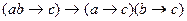 .
.
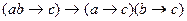 =1
=1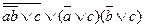 =2
=2 =3
=3
=3 =4
=4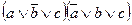 .
.
Пояснення.
1) Позбавляємось від імплікації, використовуючи тотожність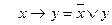 1-го пункту алгоритму.
1-го пункту алгоритму.
2) Використовуємо правило Де Моргана 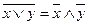 2-го пункту алгоритму.
2-го пункту алгоритму.
3) Використовуємо тотожність  з тотожностей 1 – 17 та тотожність
з тотожностей 1 – 17 та тотожність 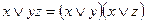 з 3–го пункту алгоритму.
з 3–го пункту алгоритму.
4) Використовуємо тотожність 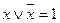 та
та 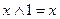 з тотожностей 1 – 17.
з тотожностей 1 – 17.
18. Рівносильні та тотожно істинні формули в бульовій алгебри
З теорем про представлення бульової функції формулою у досконалих формах випливає, що такі представлення єдині. Тому, щоб перевірити дві формули на рівносильність, достатньо звести їх до однієї із досконалих форм і порівняти.
Тотожно істинна формула в Д Д Н Ф містить 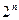 доданків, а в Д К Н Ф не містить жодної елементарної суми. Тому при дослідженні формули на тотожну істинність зведенням її до Д Д Н Ф слід перевірити присутність всіх
доданків, а в Д К Н Ф не містить жодної елементарної суми. Тому при дослідженні формули на тотожну істинність зведенням її до Д Д Н Ф слід перевірити присутність всіх 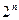 доданків. А при зведенні тотожно істинної формули до Д К Н Ф вираз спрощується і одержуємо константу 1.
доданків. А при зведенні тотожно істинної формули до Д К Н Ф вираз спрощується і одержуємо константу 1.
Тотожно хибна формула в Д К Н Ф містить 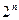 множників, а в Д Д Н Ф не містить жодного елементарного добутку. Тому при дослідженні формули на тотожну хибність зведенням її до Д К Н Ф слід перевірити присутність всіх
множників, а в Д Д Н Ф не містить жодного елементарного добутку. Тому при дослідженні формули на тотожну хибність зведенням її до Д К Н Ф слід перевірити присутність всіх 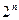 множників. А при зведенні тотожно хибної формули до Д Д Н Ф вираз спрощується і одержуємо константу 0.
множників. А при зведенні тотожно хибної формули до Д Д Н Ф вираз спрощується і одержуємо константу 0.
Приклад. Перевірити, чи рівносильні формули:  ,
,  .
.
Бачимо, що перша формула відразу ж зводиться до Д К Н Ф.  =
= =
= .
.
Зведемо і другу формулу до Д К Н Ф.  =
=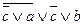 =
=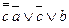 =
=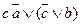 =
=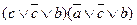 =
=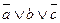 .
.
Висновок: 
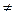
 , формули не рівносильні, нульові набори 0 0 1 та 1 0 1 відповідно.
, формули не рівносильні, нульові набори 0 0 1 та 1 0 1 відповідно.
19. Зв’язок між рівносильними і тотожно істинними формулами
Теорема. Для того, щоб формули 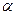 та
та  були рівносильні, необхідно і досить щоб формула
були рівносильні, необхідно і досить щоб формула 
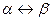 була тотожно істинною.
була тотожно істинною.
Необхідність. 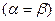
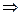
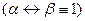 .
.
Доведення. 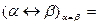
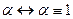 .
.
Достатність. 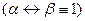
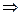
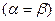 .
.
Доведемо твердження обернене до протилежного: 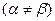
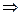
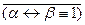 .
.
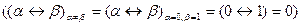
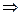
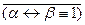 .
.
Читайте також:
- Алгебра випадкових подій
- Алгебра множин
- Алгебра подій
- Алгебраїчний спосіб визначення точки беззбитковості
- Алгебраїчні критерії стійкості
- Алгебраїчні операції
- Алгебраїчні системи
- ІІ. Алгебра висловлень
- Мінори та алгебраїчні доповнення.
- Однорідні системи лінійних алгебраїчних рівнянь.
- Основні алгебраїчні структури
| <== попередня сторінка | | | наступна сторінка ==> |
| ІІ. Алгебра висловлень | | | Необхідна та достатня умови |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |