• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Перетворення координат Лоренца.

Розглянемо дві інерціальні системи відліку: K і 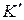, яка рухається відносно K вздовж осі Oх з швидкістю 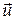(див. рис.). Нехай в початковий 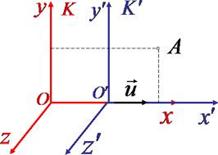момент часу 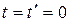, коли початки O і 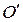збігаються, випромінюється світловий імпульс. Швидкість світла в обох системах одна і та сама і дорівнює c. Тому, якщо за час t в системі K сигнал дійде до деякої точки A, пройшовши відстань

,

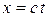то в системі 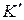координата світлового імпульсу в момент досягнення точки А

. .

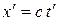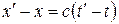Оскільки 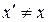, тому що система 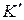переміщається відносно до системи K, то 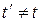. В результаті відлік часу має відносний характер.

Ейнштейн показав, що в теорії відносності перехід від однієї інерціальної системи відліку до іншої описується перетвореннями Лоренца:

, , , ;

, , , ;

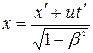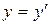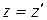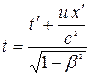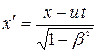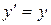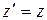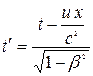де .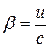

Перетворення Лоренца переходять у перетворення Галілея, якщо .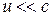

5. Релятивістський закон додавання швидкостей. Відносність довжин та проміжків часу. Інтервал між подіями.

Розглянемо рух матеріальної точки в системі 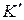, яка рухається відносно системи K із швидкістю u. Якщо в системі K рух точки в кожний момент часу t визначається координатами x, y, z, а в системі 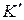в момент часу t – координатами 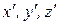, то

, , ,

, ,

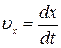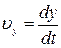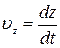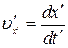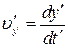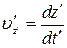
є проекціями вектора швидкості точки відносно систем K і 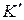на відповідні координатні осі. Використаємо перетворення Лоренца

, , ,

, .

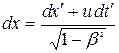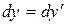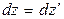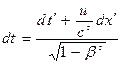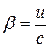Розділимо перші три рівності на четверту:

,

,

.

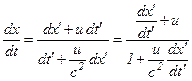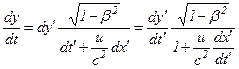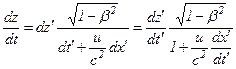В результаті отримуємо формули перетворення швидкостей при переході від однієї системи відліку до іншої:

, , .

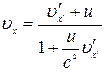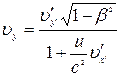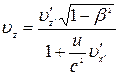Аналогічно

, , .

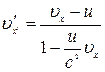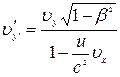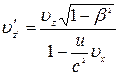Якщо матеріальна точка рухається паралельно осі Ох, то швидкість 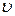відносно системи K збігається з 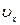, а швидкість 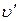відносно 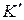– з 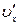. Тоді

, .

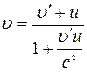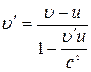Якщо швидкості 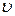, 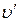і u малі порівняно з швидкістю c, то

, .

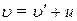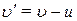Якщ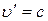о , то

.

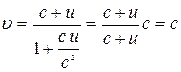Нехай .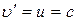

.

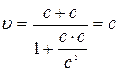При додаванні довільних швидкос­тей їх сума не може перевищити швид­кості світла c у вакуумі.

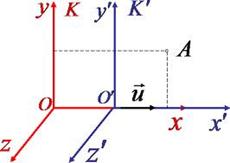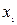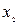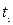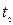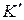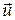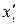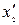Нехай в системі K в точках з координатами і в моменти часу і відбуваються дві події. В системі , яка рухається відносно K з швидкістю вздовж осі Oх, цим подіям відповідають координати і в моменти часу 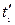і 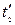(рис. ). Якщо події в системі K відбуваються в одній точці 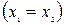і є одночасними 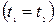, то згідно з перетвореннями Лоренца

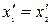і ,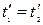

тобто ці події є одночасними і такими, що просторово збігаються для довільної інерціальної системи відліку.

Якщо події в системі K просторово розділені 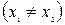, але одночасні 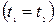, то в системі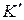

, ,

, ,

, .

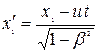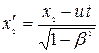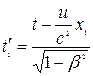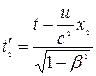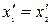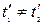Отже, в системі 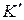ці події, залишаючись просторово розділеними, виявляються і неодночасними.

Знак різниці 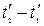визначається знаком виразу 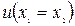, тому в різних точках системи 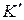(при різних u) різниця 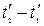буде неоднаковою за величиною і за знаком.

Нехай в деякій точці, яка нерухома в системі K, відбувається подія, тривалість якої 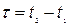. Тривалість цієї події в системі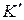

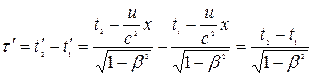
або

.

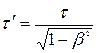Отже, 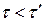і тривалість події, що відбувається в деякій точці, найменша в тій інерціальній системі відліку, відносно якої ця точка нерухома.

Отже, годинники, які рухаються відносно інерціальної системи відліку, йдуть повільніше від нерухомих годинників.

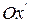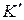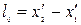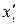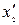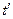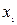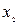Нехай деяке тіло (наприклад, стержень) розміщене вздовж осі , рухається разом з системою відліку і має в цій системі довжину , де і – координати початку і кінця стержня, які не змінюються з часом . Визначимо довжину стержня в системі K, відносно якої він рухається зі швидкістю u. Для цього треба виміряти координати його кінців і в системі K в один і той самий момент часу t:

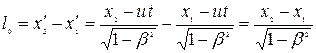
тобто

.

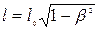Отже, довжина стрижня, яка ви­міряна в системі, відносно якої він руха­ється, є меншою від довжини, виміряної в системі, відносно якої стрижень знаходиться у стані спокою.

Поперечні розміри тіла не залежать від швидкості його руху і однакові у всіх інерціальних системах відліку.

6. Основний закон релятивістської динаміки. Релятивістський імпульс. Взаємозв’язок маси та енергії.

У релятивістській динаміці рівняння, що описують рух тіл під дією сил, повинні бути незалежними від вибору системи відліку, інваріантними відносно перетворень Лоренца. Перший постулат А.Ейнштейна вимагає збереження форми фундаментальних законів фізики в усіх інерціальних системах відліку. Фундаментальним є другий закон І.Ньютона.

А.Ейнштейн показав, що запис другого закону І.Ньютона у формі

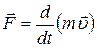
зберігається , якщо під імпульсом розуміти вираз

,

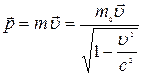де 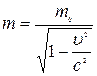– релятивістська маса частинки,

а 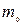– маса спокою частинки, тобто маса, яка виміряна в тій інерціальній системі відліку, відносно якої частинки знаходиться в стані спокою.

Основний закон релятивістської динаміки: швидкість зміни імпульсу матеріальної точки дорівнює силі, що діє на цю точку, тобто

.

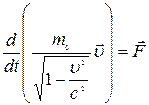А.Ейнштейн отримав закон взаємозв’язку маси і енергії – довільна зміна маси Δm супроводжується зміною повної енергії матеріальної точки:

.

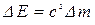Звідси А.Ейнштейн дійшов до універсальної залежності між повною енергією тіла E і його масою m:

.

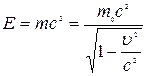Релятивістська залежність між повною енергією й імпульсом частинки:

.

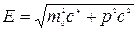Якщо тіло нерухоме, то

,

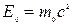де 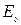– енергія спокою тіла.

Загальний висновок теорії відносності:простір і час органічно пов’язані між собою і утворюють єдину форму існування матерії – просторово-часову. Тільки тому просторово-часовий інтервал між двома подіями є абсолютним, в той час як просторовий і часовий проміжки між подіями відносні.

7. Границі застосовності класичної механіки.

Класична механіка дає точні результати для систем, які ми зустрічаємо в повсякденні. Але вони стають некоректними для систем, швидкість яких наближається до швидкості світла. Тоді класична механіка замінюється релятивістською механікою, або для дуже малих систем квантовою механікою.

Читайте також:

1. Адаптивні хвилькові перетворення : Хвилькові пакети.
2. Вантажообіг і координати магазинів, які обслуговуються
3. Визначення перетворення за Лапласом
4. Визначення скалярного добутку через координати.
5. Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
6. Визначте соціальні перетворення в процесі радянізації українського суспільства.
7. Виконаємо лінійне перетворення
8. Вимірювальні сигнали, перетворення вимірювальних сигналів, форми вимірювальної інформації
9. Вираження мішаного добутку через координати векторів.
10. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
11. Вирішення проблеми не міститься в існуючому знанні та не може бути отримане шляхом перетворення наявної наукової інформації.
12. Властивості зворотного перетворення за Лапласом

Переглядів: 1109