• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Зображення булевої функції многочленом Жегалкіна

Зобразимо будь-яку функцію формулою над базисом .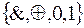

Означення. Одночленом будемо називати будь-який вираз вигляду 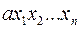, де 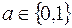. Сума за модулем 2 різних одночленів називається многочленом Жегалкіна.

Простіше кажучи, многочлен Жегалкіна – це вираз вигляду

, ,

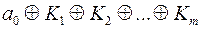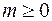де 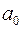– стала 1 або 0 (звичайно 0 не пишуть) і при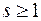 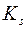– попарно різні елементарні кон’юнкції, які не містять заперечень.

Приклад многочлена Жегалкіна; .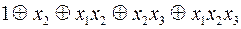

Запишемо загальне означення.

Означення. Многочленом Жегалкіна називається формула вигляду

,

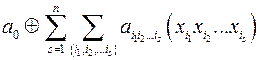де множина 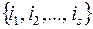перебігає всі можливі підмножини множини 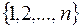, , 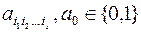а додавання відбувається за модулем 2.

Приклад. Загальний вигляд многочлена Жегалкіна від двох змінних:

.

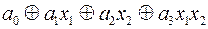Загальний вигляд многочлена Жегалкіна від трьох змінних:

.

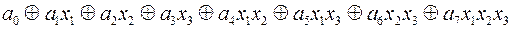Теорема (Жегалкіна). Будь-яка булева функція, відмінна від константи 0, може бути єдиним чином представлена у вигляді многочлена Жегалкіна:

=,

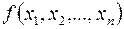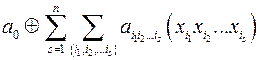де множина 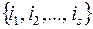перебігає всі можливі підмножини множини 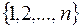, , 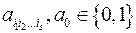а додавання відбувається за модулем 2.

(Тут єдиність розуміють з точністю до порядку доданків у сумі і порядку множників у кон’юнкціях.)

Доведення. Існування. Нехай 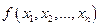– булева функція. Зобразимо її у вигляді формули через кон’юнкцию і додавання за модулем 2, використовуюси числа 0 і 1. Це можна зробити, оскільки система 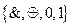є повною (приклад 7). В силу дистрибутивності кон’юнкції відносно додавання за модулем 2: 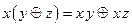, в формулі можна розкрити всі дужки і привести подібні. В результаті отримаємо многочлен від 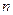змінних, який складається з членів вигляду 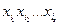, які з’єднані знаком 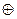, тобто многочлен Жегалкіна.

Єдиність. Доведемо єдиність представлення. Підрахуємо число різних многочленів Жегалкіна від 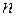змінних, тобто число варіацій виду 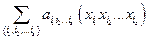. Число наборів 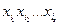дорівнює числу різних підмножин множини з 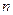елементів , сюди входить і порожня множина (при 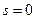). Число підмножин скінченної множини дорівнює 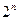, а оскільки кожен набір входить з коефіцієнтом 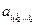, який набуває два значення: 0 або 1, то число всіх можливих многочленів дорівнює 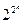, тобто числу всіх булевих функцій від 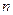змінних. Звідси випливає єдиність зображення функцій многочленом Жегалкіна. □

Існують наступні методи зображення булевої функції многочленом Жегалкіна:

1. Метод заміни. Цей спосіб зручний, коли функція задана формулою. Булеву функцію зображаємо формулою у ДДНФ над системою 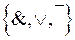і робимо заміну , .

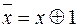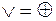Приклад. Зобразити многочленом Жегалкіна функцію, задану формулою

.

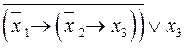Розв’язання.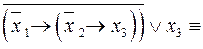

.

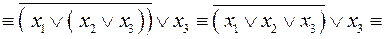
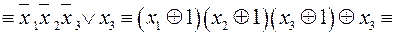
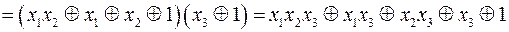Зауваження. При зведенні подібних треба пам’ятати, що парне число однакових доданків в сумі за модулем 2 дає 0.

2. Метод невизначених коефіцієнтів. Цей спосіб зручний, коли функція задана таблицею. Визначаємо коефіцієнти у загальному вигляді многочлену Жегалкіна, використовуючи значення функції на всіх наборах. Підставляємо в обидві частини різні значення змінних, отримаємо систему лінійних рівнянь (одне рівняння для кожного рядка таблиці). Розв’язавши систему, підставляємо знайдені коефіцієнти в многочлен.

Приклад. Зобразити многочленом Жегалкіна функцію 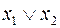, задану таблицею

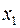
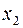
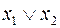
Розв’язання. Запишемо функцію у вигляді многочлена Жегалкіна від двох змінних у загальному вигляді:

=.

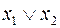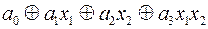Визначимо коефіцієнти, використовуючи значення функції на всіх наборах. Підставимо в обидві частини різні значення змінних 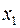, , 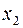отримаємо систему рівнянь (одне рівняння для кожного рядка таблиці). Розв’язавши систему, підставимо знайдені коефіцієнти в многочлен.

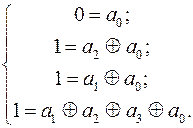
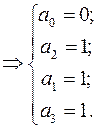
Отже, =.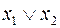

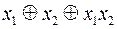3. Метод трикутника Паскаля. Цей спосіб зручний, коли функція задана вектором своїх значень. Коефіцієнти многочлена Жегалкіна можна отримати за допомогою трикутника Паскаля, побудованого за вектором значень функції, по одиницях його лівої сторони.

Приклад. Зобразити многочленом Жегалкіна функцію 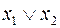, задану таблицею, за допомогою трикутника Паскаля.

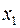
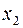
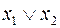
Одночлени				трикутник Паскаля
				0 1 1 1
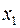
				1 0 0
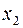
				1 0
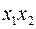
				1

Верхня сторона трикутника є вектор значень функції. Будь-який інший елемент трикутника є сума за модулем 2 двох сусідніх елементів попереднього рядка. Ліва сторона трикутника містить три одиниці. Отже, многочлен Жегалкіна буде містити три доданки. Перша одиниця трикутника відповідає набору (0 1). Отже, перший доданок многочлена Жегалкіна є 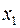. Друга одиниця трикутника відповідає набору (1 0). Отже, другий доданок многочлена Жегалкіна є 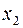. Так само для третьої одиниці. Зліва від наборів показані доданки многочлена Жегалкіна.

Остаточно маємо =.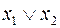

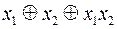Читайте також:

1. Адвокатура в Україні: основні завдання і функції
2. Алгоритм знаходження ДДНФ (ДКНФ) для даної булевої функції
3. Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції .
4. Аналіз коефіцієнтів цільової функції
5. АРХІВНІ ДОВІДНИКИ В СИСТЕМІ НДА: ФУНКЦІЇ ТА СТРУКТУРА
6. Асимптоти графіка функції
7. Базальні ядра, їх функції, симптоми ураження
8. Базові функції, логічні функції
9. Банки як провідні суб’єкти фінансового посередництва. Функції банків.
10. Банківська система та її основні функції
11. Банківська система та її структура. Функції Центрального банку.
12. Банківська система: сутність, принципи побудови та функції. особливості побудови банківської системи в Україн

Переглядів: 2971