Тривалість виготовлення книжкових полиць

Таблиця 4

Верстат	Тривалість обробки полиці моделі, хв.	Ресурс робочого часу верстатів, год. на тиждень
А	В

Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у. о., а моделі В — 30 у. о. Вивчення ринку збуту показало, що тижневий попит на книжкові полиці моделі А ніколи не перевищує попиту на модель В більш як на 30 одиниць, а продаж полиць моделі В не перевищує 80 одиниць на тиждень.

Необхідно визначити обсяги виробництва книжкових полиць цих двох моделей, що максимізують прибуток фірми.

Побудуємо економіко-математичну модель поставленої задачі та розв’яжемо її графічно.

Побудова математичної моделі. Змінними в моделі є тижневі обсяги виробництва книжкових полиць моделей А та В.

Нехай:

х₁ – кількість полиць моделі А, виготовлених фірмою за тиждень,

х₂ — кількість полиць моделі В.

Цільова функція задачі – максимум прибутку фірми від реалізації продукції: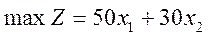

Обмеження задачі враховують тривалість роботи верстатів 1 та 2 для виготовлення продукції та попит на полиці різних моделей.

Обмеження на тривалість роботи:

для верстата 1:

30х₁ + 15х₂ ≤ 2400 (хв);

для верстата 2:

12х₁ + 26х₂ ≤ 2160 (хв).

Обмеження на попит :

х₁ – х₂ ≤ 30 та х₂ ≤ 80.

Економіко-математичну модель:

max Z = 50х₁ + 30х₂ (2.20)

за умов:

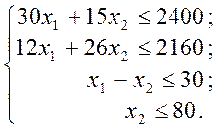
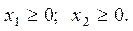
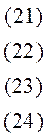
Ця економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.

Розв’язання. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис. 14). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис. 14 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

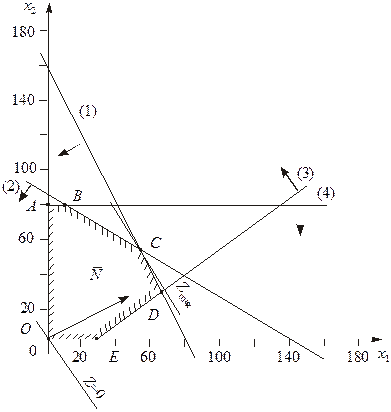
Рис. 14

Умова невід’ємності змінних х₁ ≥ 0, х₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат.

Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE.

Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’ємності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого значення.

Для цього побудуємо вектор , координатами якого є коефіцієнти при змінних у цільовій функції задачі.

Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х₁ = с₁; х₂ = с₂).

У нашій задачі вектор 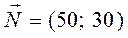. Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.

Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 50х₁ + 30х₂ = 0, яка перпендикулярна до вектора 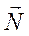і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50х₁ + 30х₂ = 0 паралельно самій собі згідно з напрямом вектора доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.

Із рис. 14 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі, тобто такими обсягами виробництва книжкових полиць видів А та В, що забезпечують максимум прибутку від їх реалізації за даних умов.

Координати точки С є розв’язком системи рівнянь (17) і (18):

звідси маємо: х₁ = 50; х₂ = 60.

Отже, Х^* = (50; 60);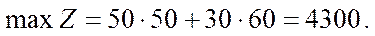

Висновок: якщо фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 — моделі В, то вона отримає максимальний прибуток – 4300 у.о., а це потребуватиме повного використання тижневих ресурсів робочого часу верстатів 1 та 2.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Розв’язати графічним методом задачу лінійного програмування	\|	Емпіричні соціологічні дослідження

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.03 сек.