• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Потенціальна енергія та її зв’язок з потенціальними силами

Нехай деяке тіло рівномірно піднімається над Землею. Рівномірне піднімання тіла можливе за рахунок дії зовнішньої сили, що зрівноважує силу тяжіння.

Кінетична енергія тіла не змінюється, бо піднімання тіла здійснюється при сталій швидкості. Виконувана зовнішньою силою робота тратиться на збільшення енергії взаємодії в системі тіло – Земля. Таку частину механічної енергії називають потенціальною .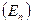

Робота А сили тяжіння дорівнює роботі зовнішньої сили взятій зі знаком мінус. Отже, можна написати, що

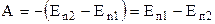. (1.67)

Зміст цієї рівності полягає в тому, що робота консервативних сил дорівнює зменшенню потенціальної енергії. Вона позволяє за відомим виразом консервативної сили знайти вираз потенціальної енергії з точністю до деякої довільної сталої. Зауважимо, що універсальної формули для вираження потенціальної енергії не має; її вираз залежить від характеру взаємодії.

Елементарна робота потенціальних сил дорівнює елементарному зменшенню потенціальної енергії

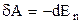або .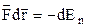

Для переміщення матеріальної точки вздовж осі маємо

.

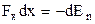Звідки (, ).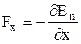

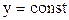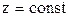Для компоненти сил по осях 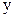і 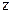отримуються аналогічні вирази. Отже,

; ; ,

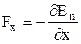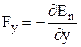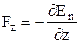або

; ; ,

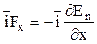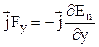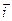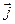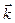(, , – орти координатних осей).

Додавши почленно ліві і праві частини цих рівностей, отримуємо

.

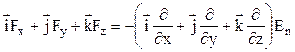Вектор 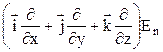називається градієнтом потенціальної енергії і позначається .

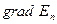Таким чином,

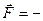gradE_n.

За отриманою формулою розв’язують обернену задачу, тобто за відомою потенціальною енергією знаходять потенціальну силу.

Читайте також:

1. Алкени – вуглеводні, в молекулах яких є один подвійний зв’язок між атомами вуглецю . Алкені називають також олефінами або етиленовими вуглеводнями.
2. Аналогія величин і рівнянь поступального і обертального руху. Кінетична енергія обертання тіла
3. Антиінфляційна політика. Взаємозв’язок інфляції та безробіття.
4. Біосфера, її складові, взаємозв’язок між ними.
5. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
6. Важливим параметром конденсаторів є пробивна напруга конденсатора. Чим вона більша, тим надійніший конденсатор, тим більша енергія може сконцентруватись на ньому.
7. Взаємозв’язок бюджету з іншими фінансовими планами
8. Взаємозв’язок витрат і доходу. «Хрест» Кейнса
9. Взаємозв’язок економічних і бухгалтерських витрат і прибутку
10. Взаємозв’язок елементів управління
11. Взаємозв’язок етики з іншими науками, що вивчають мораль
12. Взаємозв’язок з освітніми системами інших країн, відповідність вищої освіти України світовому рівню.

Переглядів: 1177