• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Лекція №2.

Лекція №1.

Література

1) А.Н.Ремезов Медична і біологічна физика:М. «Вища школа»1996г.

2) Л.Ємчик, Я.Кміт Медічна біофізика: Львів, 1998р.

3) Під ред. Проф. О.В.Чалого Медічна і біологічна фізика, Київ, 2005р.

Лекція складена доц. О.І.Івановою.

Вступ у дисципліну

“Прикладний функціональний аналіз”

1. Поняття числової множини.

2. Означення числової функції дійсної та комплексної змінної.

3. Означення границі функції та її неперервність.

План лекції

1. Дійсні числа – раціональні та ірраціональні.

2. Числові множини відрізок, інтервал, проміжок, обмежені необмежені.

3. Числова функція. Границя числової функції. Неперервність функції на мові ε-δ та на мові околів.

Лекція зрозуміла.

Поняття множини. Операції над множинами. Відображення множин.

1. Основні означення.

2. Операції над множинами.

3. Узагальнене поняття функції, як відображення та її властивості

Означення множини не має. (Пояснити чому). Позначаються множини великими буквами латинського алфавіту, а елементи множин малими буквами: Множини A, B, …;Елементи множин a, b c. Належність елемента множині позначають так: a А.

Операції над множинами.

1. Об’єднання двох множин 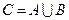. (Графічне зображення)

2. Перетин двох множин 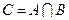. (Графічне зображення)

3. Різниця двох множин 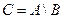. (Графічне зображення)

Властивості:

1.

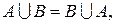
2.

3. ,

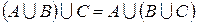4. ,

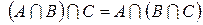5. , ,

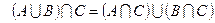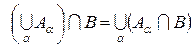6. , .

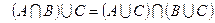7.

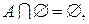
8. .

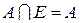Різницею множини A та B називають сукупність тих елементів в А, які не належать В, та позначають .

Доповненням 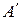множини називають сукупність тих елементів із 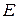, які не належать :

9. ,

10. ,

11. ,

12. ,

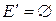13. ,

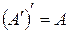14. ,

15. ,

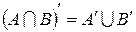Симетричною різницею двох множин A та B називають сукупність тих елементів, які визначаються наступним чином:

.

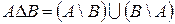Якщо А є підмножиною множини В (графічно зобразити), то позначають так: .

Відображення – узагальнення поняття функції. .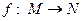

Якщ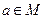о , то 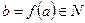називають образом елемента 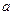. Сукупність усіх тих елементів 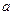, які відображаються функцією в елемент називають повним прообразом елемента та позначають .

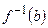Нехай множина А є підмножиною М: 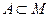. Тоді сукупність елементів 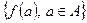називають образом множини А відображенням 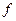і позначають . Аналогічно, для кожної підмножини В із визначається повний прообраз 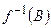множини В, тобто, це така підмножина множини М, яка відображається у множину В.

Основні властивості відображення:

Теорема 1. Прообраз суми двох множин дорівнює сумі прообразів цих множин:

Доведення. ….

Теорема 2. Прообраз перетину двох множин дорівнює перетину прообразів цих множин:

.

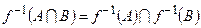Доведення. ….

Розбиття на класи. Еквівалентність Множини можна розбивати на суму підмножин, що не перетинаються. Наприклад, площину можна розбити на сукупність прямих, паралельних осі Ох. І т.д.

Розбиття здійснюється за допомогою певного признаку. Однак ці признаки повинні задовольняти певним умовам (не можуть бути абсолютно довільними). Щоб встановити властивості признаку введемо поняття відношення еквівалентності.

Нехай М – деяка множина та нехай деяка пара елементів цієї множини є відміченою: 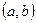. Тоді будемо говорити, що елемент 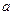пов'язаний з елементом деяким відношенням φ. Позначимо це відношення так: . Наприклад, якщо розглянути розбиття трикутників на класи по признаку рівновеликих трикутників, то означає, що площа трикутника 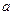дорівнює площі трикутника . Таке відношення називають відношенням еквівалентності, якщо воно задовольняє властивостям:

1. Рефлексивність: для всіх елементів .

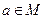2. Симетричність: якщо , то .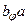

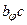3. Транзитивність: якщо та , то .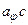

Ці умови є необхідними та достатніми для того, щоб відношення φ розбивало би множину М на класи.

Це поняття розбиття множини на класи тісно пов’язано з відображенням .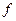

Нехай 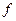– є відображенням множини А у множину В. Зібравши в один клас усі ті елементи множини А, образи яких у В співпадають, тримаємо деяке розбиття множини на класи.

Еквівалентність множин.

Упорядковані та цілком упорядковані множини.

1. Скінченні та нескінченні множини.

2. Зліченні множини

3. Еквівалентність множин. Потужність множин.

4. Упорядковані множини.

5. Цілком упорядковані множини.

Означення. Якщо у множині А скінченне число елементів, то множина скінченна. Якщо ж елементів нескінченне число, то множина нескінченна.

Скінченні множини можна порівнювати по кількості елементів. У цьому випадку множини називають еквівалентними, якщо у них однакова кількість елементів, нехтуючи їхньою природою.

Як же порівнювати між собою нескінченні множини?

Серед нескінченних множин можна виділити зліченні множини. Це такі, які можна перелічити, застосовуючи натуральні числа 1, 2, …, n, …

До зліченних множин відносяться:

1. Множина цілих чисел.

2. Множина парних чисел.

3. Множина непарних чисел.

4. Множина раціональних чисел.

Властивості зліченних множин:

1. Всяка підмножина зліченної множини є або скінченною, або зліченною.

2. Сума довільного скінченного або зліченного числа зліченних множин є зліченною множиною.

3. Всяка нескінченна множина містить зліченну множину.

Наслідок. Серед нескінченних множин зліченна є найменшою нескінченною множиною.

Еквівалентність множин.

Означення. Дві множини і 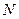називають еквівалентними, якщо між їхніми елементами можна встановити взаємно однозначну відповідність. Позначають так:

.

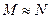У нескінченній множині можна вибрати таку нескінченну підмножину, яка буде еквівалентна даній множині. Таку підмножину називають істинною підмножиною. Наприклад, серед цілих чисел істинною підмножиною є натуральні числа.

Виявляється, що серед нескінченних множин є такі, які незліченні. До них відноситься множина дійсних чисел.

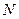Теорема Кантора-Бернштейна. Нехай і дві довільні множини. Якщо існує взаємно однозначне відображення 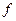множини на підмножину множини 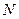та взаємно однозначне відображення 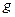множини 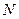на підмножину множини , то і 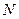еквівалентні.

Потужність множини. У скінченних множинах потужність може визначатись кількістю елементів множини. Як же визначати потужність нескінченних множин? Якщо множини еквівалентні, то у них однакова потужність. Якщо ж у множини 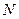елементів більше, ніж у , то потужність множини 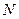буде більшою за потужність множини . Потужність зліченних множин позначають читається алеф нуль. Потужність множини дійсних чисел є континуум 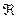. Очевидно, що 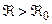. Чи існують проміжні потужності між та ?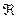

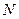Нехай і – дві довільні множини, , 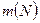– їхні потужності. Тоді можливі лише три випадки:

1. , , .

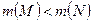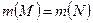Теорема3. Нехай – деяка множина та – множина усіх підмножин множини . Тоді Множина має більшу потужність ніж . Потужність множини позначають: 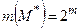, де .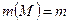

Множина усіх підмножин зліченної множини є континуумом, тобто .

Упорядковані множини.

Читайте також:

1. Вид заняття: лекція
2. Вид заняття: лекція
3. Вид заняття: лекція
4. Вид заняття: лекція
5. Вид заняття: лекція
6. Вступна лекція
7. Вступна лекція 1. Методологічні аспекти технічного регулювання у
8. Клітинна селекція рослин.
9. Колекція фонограм з голосами осіб, які анонімно повідомляли про загрозу вибуху
10. ЛЕКЦІЯ (4): Мануфактурний період світової економіки
11. Лекція - Геополітика держави на міжнародній арені
12. Лекція 02.04.2013

Переглядів: 696