Поняття бінарного відношення. Способи перетворення бінарних відношень і дії над ними

Основні поняття та операції над бінарними відношеннями

Бінарні відношення, функції та механізми вибору

Лекція 2

v Основні поняття та операції над бінарними відношеннями

v Подання системи переваг бінарними відношеннями

v Функції та механізми вибору

Бінарні відношення – теоретичне підґрунтя теорії прийняття рішень, оскільки для дослідження переваг децидента використовують основні типи бінарних відношень, а властивості бінарних відношень інтерпретуються якісно в термінах системи переваг децидента. Доведені твердження дають можливість побудувати алгоритми перевірки експериментальних відношень на наявність таких важливих властивостей, як транзитивність, ациклічність, лінійність, щоб виявляти і корегувати суперечності в міркуваннях децидента.

Апарат бінарних відношень у теорії прийняття рішень є теоретичним підґрунтям для оцінювання переваг альтернатив шляхом попарних порівнянь. Такий підхід достатньо поширений, оскільки він дає змогу виявляти переваги децидента чи експертів «у чистому вигляді»: децидентові значно простіше порівняти дві альтернативи, ніж багато.

Відношення — це твердження, що відображає взаємний зв’язок між двома чи більшою кількістю об’єктів.

Наприклад, «Ганна – сестра Івана», «число 12 більше за число 10», «золото важче, ніж алюміній», «весна та зима – пори року». Ці твердження інформують нас про те, що об’єкти належать до одного класу («діти одного батька», «пори року»), або про певний порядок об’єктів у системі («більше», «важче»). У цих прикладах об’єкти і відношення мають конкретні назви, і після підстановки інших об’єктів у твердження відношення може бути правильним або ж утратить сенс.

Отже, необхідною передумовою для побудови відношення є описання множини об’єктів, на яких воно буде визначене, тобто множини–носія відношення. Нехай А – множина певних об’єктів (наприклад, можливих варіантів рішень). Множина всіх пар (х, у), хÎА, уÎА, є декартовим добутком множини А саму на себе, А×А.

ОЗНАЧЕННЯ 2.1. Бінарним відношенням на множині А називається підмножина R Í А×А. Якщо пара (х, у) знаходиться у відношенні R, то цей факт позначається як xRy або (х, у)ÎR. Множина А називається носієм відношення R.

Приклад 2.1. Відношення R «знаходиться на колі з одиничним радіусом і центром у початку координат» записується як R = {(x, y) Î А×А | х² + у² = 1}, де А – множина дійсних чисел, що є областю визначення (носієм) відношення.

Приклад 2.2. Нехай А = В = N, де N – множина натуральних чисел. Розглянемо відношення «£», тобто R = {(m, n) | m, n Î N, m £ n}. Воно виконується для пар (5, 7), (2, 2), але не виконується для пари (5, 4).

Приклад 2.3. Нехай А = В = N. Відношення «мати спільний дільник, відмінний від 1» виконується для пар (2, 4), (3, 15), але не виконується, наприклад, для будь–якої пари (n, n + 1).

Бінарне відношення можна задати переліком пар, що перебувають у ньому, або за допомогою правила, яке дає змогу з’ясувати, чи перебуває пара в певному відношенні, чи ні.

Розглянемо основні типи бінарних відношень і можливі операції над ними в матричному та графовому представленні.

Нехай бінарне відношення R означено на скінченній n–елементній множині А. Перенумеруємо елементи цієї множини числами від 1 до n, і розглянемо квадратну матрицю В розміром n×n, у якій i–й рядок та і–й стовпець відповідають і–му елементу множини А. Визначимо елементи матриці В залежно від виконання відношення:

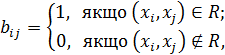
де х_i Î A, х_j Î A.

Отже, відношення R на скінченній n–елементній множині А можна задати матрицею

B(R) = ||b_ij(R)||.

Оскільки елементи множини А можна перенумерувати довільним чином і існує n! різних нумерацій, то відповідно існує n! матриць, що описують конкретне бінарне відношення. У подальшому для скорочення вживатимемо запис R замість B(R), якщо з контексту зрозуміло, що йдеться про матрицю.

Приклад 2.4. Нехай А = {1, 2, 3, 4, 5} – носій бінарного відношення «£». Для цього відношення відповідна матриця має вигляд

ОЗНАЧЕННЯ 2.2. Областю визначення бінарного відношення R називається множина

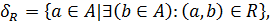
тобто до області визначення належать ті елементи множини–носія А, для яких знайдеться хоча б один елемент цієї множини, з яким вони перебувають у відношенні aRb.

Приклад 2.5. Нехай А = {1, 2, 3, 4, 5, 6, 7}, R = «£». Область визначення відношення R є .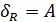

Приклад 2.6. Нехай А = {1, 2, 3, 4, 5, 6}, R = {(a, b) | a, b Î A, a = b + 3}. Тоді d_R = {1, 2, 3}.

ОЗНАЧЕННЯ 2.3. Областю значення бінарного відношення R називається множина

тобто до області значення належать ті елементи множини–носія, для яких знайдеться хоча б один елемент, який перебуває з ними у відношенні R.

Приклад 2.7. Нехай А = {1, 2, 3, 4, 5, 6}, R = {(a, b) | a, b Î A, a = b + 2). У цьому випадку d_R = {1, 2, 3, 4}, r_R = {3, 4, 5, 6}.

Поставимо у взаємно однозначну відповідність елементам множини А = {х₁, х₂, ..., х_n} вершини графа G(R) = áL, Nñ. Тут N = {1, ..., n) — множина вершин графа G, L – множина його дуг, причому L = {(і, j) | х_іRx_j}, тобто дуга в графі G з’єднує вершину і з вершиною j лише тоді, коли x_i Î A, x_j Î A перебувають у відношенні R: х_іRx_j (коли х_іRx_i, дуга перетворюється на петлю). Отже, бінарне відношення можна подати у вигляді орієнтованого графа G(R).

Відношення R можна також описати за допомогою перетенів множини А.

ОЗНАЧЕННЯ 2.4. Верхнім перетином R⁺(x) відношення R множиною–носієм А відносно елемента х називають множину

R⁺(x) = {y Î А | (у, х) Î R}.

ОЗНАЧЕННЯ 2.5. Нижнім перетином R^–(х) відношення R множиною–носієм А відносно елемента х називають множину

R^–(x) = {y Î А | (х, у) Î R}.

У літературі зустрічаються також терміни «прообраз» та позначення R^–1(х) = R⁺(x) і «образ» для R(x) = R^–(x).

Приклад 2.8. Нехай А = {1, 2, 3, 4, 5, 6}, R = «£», х = 2. Тоді R^–(2) = {2, 3, 4, 5, 6}.

Приклад 2.9. Нехай А = {1, 2, 3, 4, 5, 6}, R = «>», х = 3. Тоді R^–(3) = {4, 5, 6}.

Отже, R⁺(х) – це множина всіх елементів уÎА, таких, що знаходяться у відношенні R із фіксованим елементом х, a R^–(x) – множина всіх елементів уÎА, з якими елемент х знаходиться у відношенні R.

Щоб однозначно описати відношення R за допомогою перерізів, слід задати множину верхніх перерізів R⁺(x) для всіх елементів хÎА, або множину нижніх перерізів R^–(x) для всіх хÎА, тобто

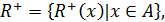
Важлива особливість цього способу завдання відношень полягає в тому, що він дає змогу представляти (зображати) відношення на нескінченних множинах. Отже, бінарні відношення можна подавати у вигляді формальних співвідношень, матриць, графів і за допомогою множин верхніх або нижніх перетинів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад 2.5	\|	Елементарні типи бінарних відношень

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.