• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

СТИСЛИЙ конспект лекцІй

Висновки

Кількість фаз, що перебувають у стані рівноваги, менша або дорівнює кількості компонентів плюс два.

Ми вивели правило фаз із співвідношення кількості змінних та кількості рівнянь. Якщо кількість змінних дорівнює кількості рівнянь, то можна знайти значення усіх змінних, і всі вони будуть мати однозначне, визначене значення. Якщо кількість рівнянь менша від кількості змінних, то не можна знайти значення усіх перемінних, можна знайти тільки зв¢язок між ними. Наприклад, якщо взяти одне рівняння з двома невідомими х + у = а, то не можна знайти значення х і у окремо. Рівняння передає тільки зв¢язок між х і у. Довільно можна міняти одну змінну, а інша буде набувати цілком визначених значень, що визначаються рівняннями. Іншими словами, існує один ступінь свободи. Якщо б було три змінних і одне рівняння, то можна було б змінювати довільно дві змінні, тобто мати два ступені свободи тощо.

У загальному випадку кількість ступенів свободи дорівнює різниці між кількістю змінних та кількістю рівнянь, що їх зв¢язують. Іншими словами, кількість ступенів свободи – це кількість змінних, які можна змінювати довільно. Значення інших змінних будуть визначатися з рівнянь. Знайдемо у відповідності до цього кількість ступенів свободи С, як різницю між кількістю змінних рівнянь:

С = 2Ф + ( К – 1)×Ф – (Ф – 1)×(К + 2)

або

С = К – Ф + 2. (6.19)

Кількість ступенів свободи рівноважної термодинамічної системи, на яку із зовнішніх чинників впливають тільки температура та тиск, дорівнює кількості незалежних компонентів мінус кількість фаз плюс два.

Це ще одне формулювання правила фаз, що найбільш часто використовується.

У окремому випадку, коли розглядають систему при постійному тиску або температурі, правило фаз набуває вигляду

С = К – Ф + 1. (6.20)

Якщо на рівновагу у системі, крім температури та тиску, можуть впливати інші зовнішні чинники, наприклад, електричні та магнітні поля, поле тяжіння на ін., то кількість зовнішніх чинників n буде більше від двох і

С = К – Ф + n. (6.21)

Кількість ступенів свободи характеризує варіантність системи, тобто кількість незалежних змінних (тиск, температура і концентрація компонентів), які можна змінювати у деяких межах так, щоб кількість і вигляд фаз залишилися без змін.

При класифікації систем їх прийнято розділяти за кількістю фаз на однофазові, двофазові тощо, за кількістю компонентів - на однокомпонентні, двокомпонентні, трикомпонентні тощо, за кількістю ступенів свободи – на інваріантні (С = 0), моноваріантні (С = 1), біваріантні (С = 2) тощо.

Дано загальну характеристику фазовим переходам. Проведена їх класифікація. Виведено рівняння Клапейрона-Клаузіуса у диференціальному й інтегральному вигляді для фазових переходів першого роду. Розглянуто практичне значення цього рівняння.

Представлені загальні умови фазової рівноваги і сформульовано правило фаз. Введено поняття числа ступенів свободи. Проведено класифікацію систем за кількістю фаз, числом компонентів і числом ступенів свободи.

Як відомо, залежно від зовнішніх умов одна й та сама речовина може перебувати у різних фазах, що відповідають різним агрегатним станам речовини. Речовина може переходити із однієї фази в іншу. Такий перехід називається фазовим переходом або фазовим перетворенням.

Фазовий перехід супроводжується низькою особливостей. Відповідно до характеру цих особливостей фазові переходи можуть бути першого та другого родів. Фазовий перехід, що характеризується однаковістю енергій Гіббса, співіснуючих у рівновазі фаз, і стрибкоподібним зміненням ентропії та об¢єму при переході речовини із однієї фази в іншу, називається переходом першого роду. Фазові переходи першого роду супроводжуються виділенням або поглинанням теплоти, яка називається прихованою теплотоюфазового перетворення DН_ф (температура залишається незмінюваною, незважаючи на підведення або відведення теплоти).

Прикладами фазових переходів першого роду є випарювання, конденсація, плавлення, кристалізація, сублімація, а також переходи твердих речовин із однієї кристалічної модифікації в іншу (перехід сірого олова у біле, графіту у алмаз, моноклінної сірки у ромбічну тощо).

Крім фазових переходів першого роду, існують фазові переходи другого роду. Для них характерна не тільки однаковість енергій Гіббса, але й однаковість ентропій та об¢ємів співіснуючих у рівновазі фаз, тобто відсутність теплового ефекту процесу та змінення об¢єму при температурі перетворення. Зате мають місце стрибки фізичних величин, що виражені похідними ентропій та об¢єму: теплоємність С = T(dS/dT)_P та коефіцієнт термічного розширення

b = ∙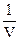

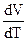
Прикладами фазових переходів другого роду є перехід речовини у надпровідниковий стан, перехід парамагнетику у ферромагнетик, перехід рідкого гелію у надтекучий стан.

Рівняння Клапейрона-Клаузіуса відображає особливості фазових переходів першого роду. Для процесу випарювання

DН_в = T(V_п –V_р).

Це рівняння Крапейрона-Клаузіуса у диференціальному вигляді. Його можна записати і для інших фазових переходів. Так, для возгонки (сублімації)

DН_С = T(V_п –V_т ) .

Для плавлення

DН_пл = T(V_р –V_т ) .

Для фазових переходів з участю пари (випарювання, сублімація, конденсація) отримане рівняння Клапейрона-Клаузіуса можна перетворити у більш зручне для практичного використання рівняння. Для цього необхідно зробити такі припущення:

1 Пар мати за ідеальний газ, для одного моля якого PV = RT;

2 Знехтувати мольним об¢ємом рідкої або твердої речовини порівняно до мольного об¢єму пари (V_п»V_р або V_п»V_т);

3 Знехтувати залежністю теплоти фазового переходу від температури (це справедливо для невеликих інтервалів температур).

Отримаємо для процесу випарювання

.

Для процесу сублімації

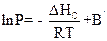
Рівняння показують, що логарифм тиску пари над твердою і рідкою речовиною лінійно залежить від зворотної температури.

Розглянемо тепер рівновагу між фазами, тобто гетерогенну рівновагу. Нехай у системі співіснують Ф фаз, кожна з яких складається із К компонентів. Система перебуває у гетерогенній рівновазі, коли всі фази будуть у термодинамічній, механічній та хімічній рівновазі. Термічна рівновага виражається однаковістю температури у всіх фазах, механічна – тисків, хімічна – однаковістю хімічних потенціалів.

Т₁ = Т₂ = Т₃ = … = Т_ф,

Р₁ = Р₂ = Р₃ = … = Р_ф,

m₁¹ = m₂¹ = m₃¹ = … = m_ф¹,

m₁² = m₂² = m₃² = … = m_ф²,

…………………………..,

m₁^к = m₂^к = m₃^к = … = m_ф^к.

Розрахуємо тепер кількість незалежних змінних, що входять до складу цих равенств та кількість рівнянь, що зв¢язують ці змінні. Кількість рівнянь не може перевищувати кількості перемінних, оскільки у противному разі рівняння будуть наслідками одне одного або несумісними. Тому можна записати Ф£К+2. Це одна з форм запису правила фаз:

Читайте також:

1. Види лекцій
2. Викладення лекційного матеріалу
3. ГИСТОЛОГИЯ. КОНСПЕКТ ЛЕКЦИЙ.
4. Електронний конспект лекцій
5. Завдання лекційних занять
6. І. ПРОСЛУХОВУВАННЯ ТА КОНСПЕКТУВАННЯ ЛЕКЦІЙ
7. ІІ. МАТЕРІАЛИ ДО КУРСУ ЛЕКЦІЙ
8. ІІI. Тематика лекцій
9. ІІІ. ПЛАН ПРОВЕДЕННЯ ЛЕКЦІЙНОГО ЗАНЯТТЯ
10. Індивідуальний метод обліку кількості знесених яєць проводять у селекційних стадах, застосовують для цього контрольні гнізда, або утримання в індивідуальних клітках.
11. Коновалова М.Д.Экспериментальная психология: конспект лекций. - Высшее образование. – 2006.
12. КОНСПЕКТ

Переглядів: 718