• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

В. Друга теорема про розклад.

Б. Перша теорема про розклад.

Теорема 1. Якщо ряд Лорана зображення функції має вигляд

,

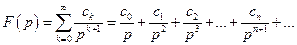то .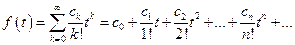

Приклад 3. Знайти оригінал функції 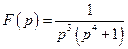, використовуючи першу теорему розкладу.

Розв’язання. Маємо , якщо .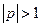

Тоді, .

Приклад 4. Знайти оригінал функції .

Розв’язання. Маємо . Тоді, .

Нехай 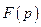– дробово-раціональна функція, тобто вона є відношенням двох многочленів

,

де 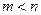і коефіцієнти 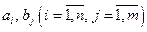– дійсні числа. Знайдемо всі корені многочлена у знаменнику і розкладемо його на множники. Тоді

,

де – корінь знаменника кратності (полюс порядку функції ).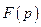

Теорема 2. Якщо 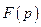– правильна дробово-раціональна функція, полюси якої , то

.

З теорії лишків відомо, що 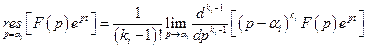, тому .

Приклад 5. Знайти оригінал за зображенням .

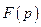Розв’язання.Подамо це зображення у вигляді . Точки та є полюсами функції другого порядку. Обчислимо лишки функції в цих точках:

,

.

За другою теоремою розкладу

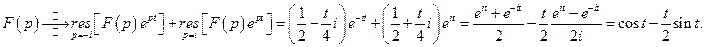
Застосування операційного числення

1. Розв’язування лінійних диференціальних рівнянь

зі сталими коефіцієнтами операційним методом.

Розглянемо задачу Коші для лінійного диференціального рівняння 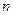-го порядку зі сталими коефіцієнтами: знайти розв’язок рівняння

,

що задовольняє початкові умови

.

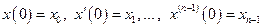Загальна схема розв’язування задачі Коші для лінійних диференціальних рівнянь зі сталими коефіцієнтами операційним методом:

1) від диференціального рівняння і початкових умов прямим перетворенням Лапласа переходимо до рівняння в зображеннях, яке називається операторним рівнянням;

2) розв’язуємо отримане алгебраїчне рівняння, тобто знаходимо зображення шуканого розв’язку;

3) переходимо від зображення розв’язку до шуканого розв’язку в просторі оригіналів.

Приклад 1. Знайти розв’язок задачі Коші , .

Розв’язання. Нехай . Тоді

, , .

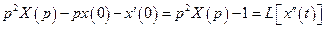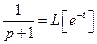Операторне рівняння має вигляд 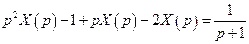, звідки

.

Оскільки , то розв’язок задачі Коші .

Припустимо, що потрібно знайти розв’язок рівняння

,

що задовольняє початкові умови

.

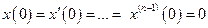Якщо відомо 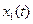розв’язок відповідного рівняння при з тими ж початковими умовами, то

Справді, при переході до операторних рівнянь матимемо

,

.

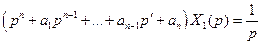Поділивши ці рівності отримаємо, що 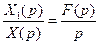, тобто . Залишилось скористатися формулою Дюамеля і врахувати, що .

Приклад 2.Знайти розв’язок задачі Коші ,

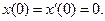
Розв’язання. Розглянемо рівняння 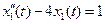. Відповідне операторне рівняння має вигляд

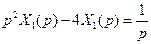. Тоді , а отже,

Тоді

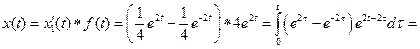
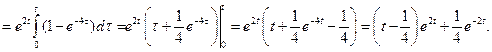
1. Розв’язування систем лінійних диференціальних рівнянь

зі сталими коефіцієнтами операційним методом.

Розглянемо задачу Коші для системи лінійних диференціальних рівнянь з сталими коефіцієнтами вигляду

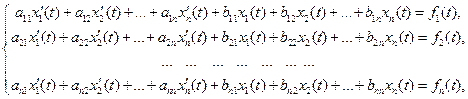
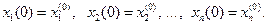
Якщо до цієї системи застосувати перетворення Лапласа, то отримаємо лінійну систему алгебраїчних рівнянь відносно невідомих Розв’язавши отриману систему для знаходження розв’язку вихідної системи залишається лише повернутись від зображень до їх оригіналів.

Приклад 1.Знайти розв’язок

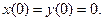
Розв’язання. Відповідна система операторних рівнянь має вигляд

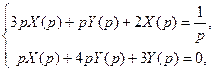або

Застосуємо метод Крамера:

Тоді

Отже,

Читайте також:

1. I. Грецький період (друга половина VII — середина
2. Вересня 1939 р. з нападу фашистської Німеччини на Польщу розпочалася Друга світова війна.
3. Друга акція громадської непокори.
4. Друга група показників (непрямі).
5. Друга екваторіальна система координат
6. Друга закономірність: пропорційність виробництва і управління.
7. Друга контрольна робота
8. Друга контрольна робота
9. Друга модульна контрольна робота
10. Друга модульна контрольна робота
11. Друга науково-технічна революція

Переглядів: 2011