Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Статистичне вивчення варіації.

План.

1. Суть варіації. Необхідність її статистичного вивчення.

2. Характеристики або показники варіації.

3. Методи обчислення дисперсії.

4. Види дисперсії. Правила додавання дисперсій.

5. Характеристики форми розподілу.

6. Криві розподілу.

До характеристик варіації відносяться наступні показники: розмах варіації, середнє лінійне відхилення, середній квадрат відхилення, середнє квадратичне відхилення, коефіцієнти варіації.

Найпростішим показником варіації є її розмах (R). Його визначають як різницю відхилення між максимальним і мінімальним значенням ознаки.

R= X_max – X_min

Розмах варіації використовується в тих випадках, коли важливо встановити амплітуду варіації ознаки. Для прикладу: оцінити варіацію цін на товари за певний проміжок часу, встановити зміну попиту на продукцію.

Точнішою характеристикою варіації ознаки служить середнє лінійне відхилення. Показник середнього лінійного відхилення будується на припущенні, що в однорідній сукупності типовою, однаковою для всіх одиниць ознакою може бути її середнє значення.

Залежно від інформації середнє лінійне відхилення (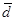) вираховується за наступними формулами:

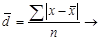для індивідуальних показників;

для показників у згрупованій сукупності.

Середнє квадратичне відхилення, як і середнє лінійне відхилення., служить абсолютною мірою варіації. Середнє квадратичне відхилення обчислюють за формулою:

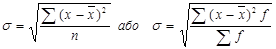Дисперсія являє собою середній квадрат відхилень індивідуальних значень ознаки від їх

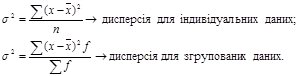середньої величини і визначається за такими формулами:

Показники варіації - розмах варіації, середнє лінійне відхилення, дисперсія та середнє квадратичне відхилення - є абсолютними величинами, і завжди виражаються в одиницях виміру досліджуваного явища. Між вказаними абсолютними показниками зберігаються конкретні співвідношення при умові нормального розподілу одиниць в сукупності за конкретною ознакою: 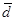≈ 0,8 σ або σ ≈ 1,25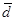

Розрізняють такі відносні показники варіації:

- коефіцієнт осциляції VR;

- лінійний коефіцієнт варіації Vd;

- коефіцієнт варіації γ.

Формули відносних показників варіації:

Коефіцієнт варіації γ використовується як показник однорідності сукупності. Вважається, що при γ ≤ 33% сукупність є однорідною, а отже, 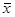– типовою і надійною характеристикою сукупності.

Правило додавання дисперсій

Виділяють три види дисперсії: загальну, групову і міжгрупову.

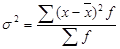Загальна дисперсія σ² характеризує варіацію ознаки під впливом усіх, без винятку, умов і факторів, які обумовили цю варіацію. Як відомо, вона визначається за формулами:

Загальна дисперсія визначається для всіх, без винятку, одиниць сукупності. Якщо сукупність поділяється на групи, то зрозуміло, що в окремих групах також можна визначити свою дисперсію. Дисперсія ознаки в групах буде знаходитися під впливом тільки тих факторів і умов, що діють всередині групи.

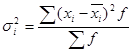Групова дисперсія (σ²і) характеризує варіацію ознаки окремих частин або груп загальної сукупності. Вона є частиною загальної варіації, обумовленою впливом неврахованих факторів, і не залежить від ознаки – фактора, закладеного в основу групування.

де: 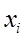- величина ознаки в ігрупі;

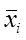- середня ознаки в кожній окремій групі.

У наведеній формулі групової дисперсії чітко видно, що вона враховує тільки квадрати відхилень групової ознаки від середньої групової. Після обчислення групових дисперсій обчислюють середню внутрішньо групову дисперсію (остаточну) за такими формулами ():

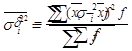Міжгрупова дисперсія (δ²) характеризує варіацію результативної ознаки за рахунок групувальної ознаки. Вона є середнім квадратом відхилень групових середніх від загальної середньої, тобто

де 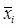середня для і-ї групи, ¯х – середня для сукупності

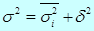Між наведеними видами дисперсій існує співвідношення: загальна дисперсія дорівнює сумі середньої із групових та міжгрупової дисперсій:

У прийнятих символах це співвідношення відоме як правило додавання дисперсій.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.