• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Критерій Пірсона. Критерій Колмогорова

Нехай випадкова величина X розподілена за законом F (x_i; q_j) і нехай на ос­нові вибірки х₁, х₂, .... , х_n, здобутої із генеральної сукупності з функцією розпо­ділу F (x_i; q_j), робимо деякі припущення (гіпотези): або про вид функції F (x_i; q_j), або про параметри q_j цієї функції. Припущення такого роду називаються статистичними гіпотезами.

Статистична гіпотеза називається параметричною, якщо в ній сформульовані припущення відносно значень параметрів функції розподілу відомого виду, непараметричною - якщо в ній сформульовані припущення відносно виду самої функції розподілу. Статистичні гіпотези поділяються на нульові Н₀ (основні) і альтернативні Н₁ (конкуруючі).

Перевірка статистичних гіпотез здійснюється на основі даних вибірки. Для цього застосовують певну виборчу статистику К, яка є функцією спостережених значень, точний або приблизний розподіл якої відомий. Випадкову величину К, за допомогою якої приймається рішення про прийняття або відхилення нуль - гіпоте­зи, називаються статистичним критерієм. Статистичним критерієм значущості називається правило відхилення нульової гіпотези, яке заключається в розбитті області можливих значень випадкової величини К на дві під області, що не перетинаються, причому нульова гіпотеза відхиляється, якщо спостережне значення критерію К на­лежить критичній під області і вважається узгодженою з дослідним, якщо К не на­лежить критичній під області. При цьому, так як рішення приймається на основі ви­бірки скінченого об'єму, дослідник може зробити слідуючи помилки: а) прийняти невірну гіпотезу (помилка першого роду); в) відхилити вірну гіпотезу (помилка другого роду).

Ймовірність зробити помилку першого роду Р (Н₁/ Н₀) = α – називається рів­нем значущості статистичного критерію. Величину 1 - Р (Н₁/ Н₀) = 1 - β називають потужністю критерію.

Перевірка гіпотези про припущений закон розподілу проводиться за допомогою непараметричних критеріїв значущості. Основна група непараметричних критеріїв значущості - критерії згоди, за допомогою яких перевіряються нульові гіпотези від­носно загального вигляду функцій розподілу. Задача визначення критерію згоди ставиться у такий спосіб: нехай х₁, х₂,..., х_n – випадкова вибірка, тобто спостережені значення випадкової величини X, і нехай f*(х) – статистична щільність розподілу; за­дамо деяку невід'ємну міру D відхилення емпіричної функції f*(х) від гіпотетичної теоретичної функції f(х).

D = D{f*(х),f(х)}.

Найбільш поширені критерії згоди: критерій Пірсона χ², λ – критерій Колмогоро­ва.

Критерій згоди Пірсона χ².

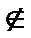Нехай випадкова величина має функцію розподілу ймовірностей F (х), яка належить деякому класу функції Ω визначеного виду (нормальних, показникових, біномінальних та інших) і нехай з генеральної сукупності вилучена вибірка об'єму n: х₁, х₂,..., х_n. Треба перевірити нульову гіпотезу Н₀: F(x) Ω при конкуруючій гіпотезі Н₁: F(x) Ω.

Схема міркувань при перевірці гіпотези Н₀ за допомогою критерію згоди Пір­сона складається з подальшого: висуваємо гіпотезу Н₀: X ~ N(α;σ) випадкова величина розподілена за нормальним законом, при конкуруючій гіпотезі Н₁: X ~ N(α;σ), випадкова величина не розподілена за нормальним законом.

Для перевірки гіпотези:

1) Складають згрупований статистичний ряд.

2) Обчислюють ймовірності попадання випадкової величини X у часткові інтервали (x_j-1; x_j) ,для цього треба попередньо пронормувати величину, тобто знайти значення . P_j = P{x_j-1 < X < x_j} = P{u_j-1 <X <u_j}= Ф(u_j) –Ф(u_j-1).

3) Визначають теоретичні частоти пр_і часткових інтервалів.

4) Обчислюють вибіркову статистику (критерій)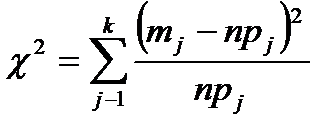

Якщо нульова гіпотеза вірна, то при n → ∞ закон розподілу даної статистики χ², незалежно від виду функції F (х), прямує до закону розділу χ² з числом ступе­нів вільності f = k - r - 1 (k – кількість інтервалів; r – кількість параметрів гіпотетич­ної функції F (х)).

5) По таблицям χ² – розподілу (див. додатки), по заданому рівню значущості a і кількості степе­нів вільності f = k - r - 1 (для нормального розподілу r = 2) знаходять критичне значення χ_a ²(f) порівнюючи значення вибіркової статистики χ², що спостері­гається з критичним значенням χ_α² (f) і приймають одне з двох рішень:

- якщо χ² < χ_α² (f) , то не існує потреби для відхилення нульової гіпотези;

- якщо χ² ≥ χ_α² (f) , то приймається конкуруюча гіпотеза Н₁.

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. IV. Критерій питомої потенціальної енергії деформації формозміни
3. ReM – модифікований критерій Рейнольда, який визначається за формулою
4. Багатокритерійні завдання і можливі шляхи їхнього рішення.
5. Деякі практичні підходи до вирішення багатокритерійних завдань.
6. Екстремум функції багатьох змінних. Необхідна та достатня умови екстремуму. Критерій Рауса-Гурвіца
7. Інженерний варіант аксіом Колмогорова
8. Когнітивний критерій
9. Критерій дисперсійного аналізу.
10. Критерій згоди Колмогорова
11. Критерій згоди Романовського
12. Критерій Колмогорова

Переглядів: 955