• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Правило №3.4

Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение,

необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.

Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке 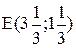, используем правило №3.4. Подставляем в левую часть ограничения (4) координаты точки Е, получаем

.

Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность полученного ранее решения, равен 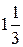т краски в сутки.

Экономический смысл ограничения (3)

в том, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки Е. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка Е остается оптимальной, является пересечение с точкой Е (см. рис.3.1). Согласно правилу №3.4, подставим координаты точки 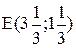в левую часть ограничения (3)

[т краски].

Получаем, что разность спросов на краску 2-го и 1-го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку Е означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1-го вида

[т краски/сутки].

Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке Е не изменится, составляет 2 т краски в сутки.

Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.3.1.

Таблица 3.1

Читайте також:

1. Аверсивную терапію використовують, як правило, при лікуванні алкоголізму, нікотиновій залежності і деяких інших захворювань.
2. Будучи, як правило, дочірніми фірмами великих компаній, вони існують за рахунок засобів венчурного капіталу і здійснюють чітко визначений вид діяльності.
3. В цілому сукупність суспільного продукту – це сукупність благ і послуг, вироблених суспільством за певний період часу (як правило, за рік).
4. В цілому сукупність суспільного продукту – це сукупність благ і послуг, вироблених суспільством за певний період часу (як правило, за рік).
5. Гарантії реалізації конст прав і свобод в ЗК. Правило Міранди,Мандамус,habeas corpus.
6. До основних засобів, як правило, не належать
7. Зайнятість – це ді-сть громадян, пов’язана із задоволенням особистих та суспільних потреб і така, що, як правило, приносить їм дохід у грошовій або іншій формі.
8. Зайнятість – це діяльність громадян, пов’язана із задоволенням особистих та суспільних потреб і така, що , як правило, приносить дохід у грошовій формі.
9. Заробітна плата – це винагорода, обчислена, як правило, у грошовому виразі, яку за трудовим договором власник або уповноважений ним орган виплачує працівникові за виконану роботу.
10. Золоте» правило інвестування.
11. І ми пам’ятаємо правило: Від живого споглядання до абстрактного мислення, і від нього до практики – такий є діалектичний шлях пізнання об’єктивної реальності.
12. Істотними умовами договору купівлі-продажу за загальним правилом є умови щодо предмету.

Переглядів: 522