• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Багатокрокове прогнозування

Багатокрокове прогнозування застосовують лише для явищ, ознаки яких представлені у вигляді часових рядів.

Для однопараметричної задачі прогнозування навчальна множина матиме вигляд наведений в табл. 3. Під час навчання мережа налаштовує коефіцієнти ваг зв'язків і поліномів передатних функцій, які в подальшому і визначають режим функціонування. Багатокрокове прогнозування часового ряду здійснюється наступним чином (рис. 12). На входи нейромережі подається вектор відомих значень x(t_n-2), x(t_n-1), x(t_n). На виході формується прогнозована величина x*(t_n+1), яка визначає вектор прогнозованих виходів і одночасно долучається до значень навчальної множини, тобто, приймається як достовірна. Далі на входи подається вектор x(t_n-1), x(t_n), x*(t_n+1), а на виході отримується x*(t_n+2) і наступні прогнозовані значення.

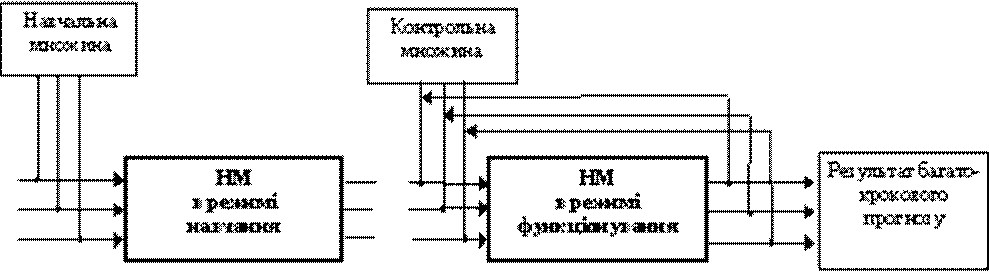
Рис. 12. Послідовність використання НМ для задач багатокрокового прогнозування

Для багатопараметричної задачі прогнозування на входи навченої нейромережі подаються вектори x(t_n-2), y(t_n-2), z(t_n-2), x(t_n-1), y(t_n-1), z(t_n-1), x(t_n), y(t_n), z(t_n). На виході продукуються величини x*(t_n+1), y*(t_n+1), z*(t_n+1), які формують вектор вихідних значень і послідовно долучаються до значень навчальної множини. При зсуві вікна на крок прогнозу вихідні дані, що були спродуковані мережею, сприймаються як реальні і приймають участь у прогнозуванні наступного значення виходу, тобто на входи подаємо вектор x(t_n-1), y(t_n-1), z(t_n-1), x(t_n), y(t_n), z(t_n), x*(t_n+1), y*(t_n+1), z*(t_n+1), а на виході отримуємо x*(t_n+2), y*(t_n+2), z*(t_n+2) і наступні прогнозовані значення.

Багатокрокове прогнозування дозволяє робити коротко- та середньотермінові прогнози, оскільки суттєвий вплив на точність має накопичення похибки на кожному кроці прогнозування. При застосуванні довготермінового багатокрокового прогнозування спостерігається характерне для багатьох прогнозуючих систем поступове затухання процесу, фазові зсуви і інші спотворення картини прогнозу. Такий тип прогнозування підходить для часових рядів, які підпадають під означення стаціонарного процесу з невеликою випадковою складовою.

Читайте також:

1. Аварійне та довгострокове прогнозування хімічної обстановки
2. Багатокрокове прогнозування з перенавчанням нейромережі на кожному кроці прогнозу
3. Бюджетне планування та прогнозування.
4. Бюджетне прогнозування
5. Визначення потреби організації у персоналі як основа для прогнозування і планування його розвитку
6. Досвід бюджетного прогнозування.
7. Екологічне прогнозування
8. Е_4. Пояснення і прогнозування моделей
9. Завдання демографічного прогнозування
10. Загальні функції управління, пов’язані з прогнозуванням, плануванням, регулюванням, координацією та контролем
11. Здійснення прогнозування, перспективного і поточного планування потреби в кадрах, їхній прямування, добору і розміщення

Переглядів: 1144