• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Редукування лінійних вимірів

Якщо - виміряна похила віддаль між віддалеміром на пункті і відбивачем на пункті , приведена до центрів знаків, то для редукування її на референц-еліпсоїд обчислюються геометричні поправки, зміст яких зрозумілий із рис. 7.1

Поправка за нахил лінії

Визначається на основі відомої формули

,

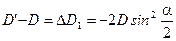де - кут нахилу даної лінії. Зважаючи на те, що кут нахилу є малою величиною, отримаємо

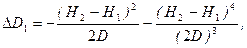(7.1)

тут

Рис. 7.1

У формулах (7.1): і 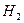- геодезичні висоти відповідно віддалеміра та відбивача; - висоти пунктів А і над квазігеоїдом; - висоти квазігеоїда над референц-еліпсоїдом.

Поправка за висоту

Визначається дана поправка із подібних трикутників та

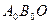
(7.2)

де 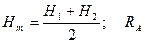- радіус кривини нормального перерізу еліпсоїда, що відповідає заданій лінії. Величину з достатньою точністю можна обчислити за формулою

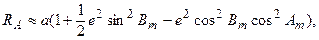(7.3)

де - широта середньої точки лінії; - середній азимут лінії.

Тоді довжина хорди =буде визначатися на основі формули

(7.4)

Введемо кут 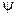при центрі сфери 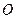(див. рис. 7.1). Отримаємо

. (7.5)

Із трикутника маємо

.

Довжина хорди буде дорівнювати

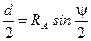. (7.6)

Враховуючи, що

,

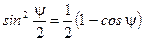остаточно отримаємо інший вигляд формули для обчислення довжини хорди

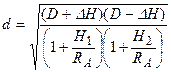, (7.7)

де , а обчислюється за формулою (7.3).

Для обчислення довжин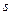и дуги скористаємося формулами (7.5) та (7.6). Шляхом розкладу малого кута в ряд отримаємо

(7.8)

Наведені вище формули можна використовувати для редукування відстаней до сотні кілометрів.

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
3. Аналіз трифазного з’єднання з урахуванням опорів лінійних проводів
4. Вимірювання лінійних переміщень, вібрацій та деформацій
5. Вимірювання лінійних та кутових розмірів
6. Вимірювання лінійних та кутових розмірів
7. Довірчий інтервал характеризує точність вимірів даної вибірки, а довірча імовірність – достовірність виміру.
8. Загальні методи кодування і декодування систематичних блокових лінійних кодів
9. Звісно ж, це забезпечує величезні можливості людського самопізнання, осягнення таких суто людських вимірів буття, як спілкування, моральність, творчість тощо.
10. Зв’язок кутових та лінійних величин
11. Квантові межі точності вимірів
12. ЛЕКЦІЯ 7. Аналіз коефіцієнтів лінійних моделей

Переглядів: 966