
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Метод координат на прямій та його застосування
Розглянемо горизонтальну пряму лінію l на площині (мал.1). На цій прямій l візьмемо нерухому
О  А1 l точкуO,що називається початком
А1 l точкуO,що називається початком

відліку. Ця точка розбила пряму на два взаємно протилежні на-
прямки: додатній – вправо і від’ємний – вліво. Взявши деяку одини-цю масштабу, вправо від точки Oвідкладаємо додатні числа, а вліво
– від’ємні числа. Ці числа відповідають деяким точкам на прямій l і навпаки, отже між точками прямої l та дійсними числами існує взаємно однозначна відповідність. Таку пряму l будемо називати числовою віссю Ox. Точці O, що вважається початком відліку , відповідає число нуль.
Таким чином, ми побудували систему координат на прямій. Візьмемо деяку точку А на числовій осі. Цій точці відповідає деяке число х, яке називається координатою точки А. Це записується А(х).
Будемо вважати відрізокОА1 , що відкладений праворуч від точки O за додатній, а відрізокОА2 відкладений ліворуч від точки О-за від’ємний(мал.1).


Відрізок, у якого A початок, а В кінець, позначають АВ і на-

зивають напрямленим відрізком. Величину відрізка AB будемо позначати символом АВ.

Означення. Відрізки, які характеризуються не тільки своєю довжиною, але й напрямом називаються напрямленими відрізками.
Величина напрямленого відрізка є його довжина, взята з пев-
| ним знаком. | x -ів дві точки A1 | і A2 відповідно з коорди- | |||||||||||||||||||||||
| Візьмемо на осі | |||||||||||||||||||||||||
| натами x1 і | x2 ,тоді і відрізкам | і | будуть відповідати числа | ||||||||||||||||||||||
| ОА1 | ОА2 | ||||||||||||||||||||||||
| x1 і x2 (мал.2). | О | А1 | А2 | х | |||||||||||||||||||||
| Покажемо, що при будь- | Мал.2 | ||||||||||||||||||||||||
| якому розташуванні точок A1 і | |||||||||||||||||||||||||
| A2 відносно | точкиО | величина | відрізка | A1 A2 | буде | ||||||||||||||||||||
| дорівнювати x2 − x1,тобто | |||||||||||||||||||||||||
| A1 A2 = x2 − x1 | (2.1) | ||||||||||||||||||||||||
| Дійсно, нехай точки | A1 і | A2 розташовані так як на мал.2. | |||||||||||||||||||||||
| Тоді A1A2 = ОА2 − ОА1 = x2 − x1. | |||||||||||||||||||||||||
| Коли точки A1 | і A2 розташовані так, як на мал.3, | ||||||||||||||||||||||||
| то | А1 А2 = А1О − А2О; | але | |||||||||||||||||||||||
| А1 | А2 | О | х | А1О =−ОА1 і А2О =−ОА2 | |||||||||||||||||||||
| Мал.3 | Одержимо | ||||||||||||||||||||||||
| А1 А2 =−ОА1 − ( −ОА2 ) = x2 − x1 . | |||||||||||||||||||||||||
| Нехай A1 і A2 розташовані | А1 | ||||||||||||||||||||||||
| по різні сторони відносно | точки | х | |||||||||||||||||||||||
| О | А2 | ||||||||||||||||||||||||
| О (мал.4). | Мал.4 | ||||||||||||||||||||||||
| Значить А1А2 = А1О + ОА2 = ОА2 − ОА1 = x2 − x1 . | |||||||||||||||||||||||||
| Якщо | x1 = 3, а | x2 =−5 , | то | величина відрізка буде | |||||||||||||||||||||
| А1 А2 =−5 − 3 =−8. | |||||||||||||||||||||||||
| Довжина відрізка А1А2 позначається через | А1 А2 | і дорівнює | |||||||||||||||||||||||
| А1 А2 | = | x2 − x1 | (2.2) | ||||||||||||||||||||||



Висновок.Якщо на прямій в деякій системі координат заданодві точки A1( x1) і A2( x2) ,тоді величина відрізка A1A2 знаходиться
із рівності (2.1), а віддаль (довжина) між цими точками за формулою
(2.2).
Приклад 1.Задано точкиA( 2 ), B(−7 ), C(−3 ).
Знайти величину відрізків АВ , СВ .
| Розв’язування. За формулою(2.1)одержуємо: AB =−7 − 2 =−9 . | |||||||||
| СВ =−7 − ( −3 ) =−7 + 3 =−4. | |||||||||
| Приклад 2.Знайти віддаль між точкамиA( 3 ), B(7 ). | |||||||||
| Розв’язування. | За | формулою | (2.2) | одержимо | |||||
| d = АВ = 7 − 3 = 4. | |||||||||
| §2. Прямокутна система координат на площині | |||||||||
| та її застосування | |||||||||
| Положення точки на прямій, як ми бачили, визначається од- | |||||||||
| ним числом – її координатою, а положення точки на площині, як ми | |||||||||
| побачимо, визначається упорядкованою парою чисел (тобто вказано | |||||||||
| яке із чисел є першим, а яке другим). | |||||||||
| Візьмемо на площині дві взаємно перпендикулярні осі і на- | |||||||||
| у | звемо їх осями координат (мал.5). | ||||||||
| М | Точка перетину осей координат O | ||||||||
| N1 | називається | початком | координат. | ||||||
| ІІ | І | Осі координат ( Оx - вісь абсцис, | |||||||
| горизонтальна, | Oy −вісь ординат, | ||||||||
| О | М1 | х | вертикальна ). Осі координат Оx і | ||||||
| Мал.5 | ІІІ | ІV | Oy ділять площину на чотири час- | ||||||
| тини, які називаються квадрантами | |||||||||
| ( або координатними кутами). Частина площини, що міститься між | |||||||||
| додатними осями Оx і Oy | називається | першим | квадрантом. | ||||||
| Нумерація квадрантів іде проти годинникової стрілки. | |||||||||
| Нехай точка М - | довільна точка площини. Опустимо з цієї | ||||||||
| точки | перпендикуляри | на | вісь Оx і Oy , основи цих | ||||||
| перпендикулярів | позначимо | відповідно | через | М1 і N1 , | тобто | ||||
| М1 і N1 | є проекціями точки М на координатні осі. Позначимо ко- | ||||||||
| ординату точки | М1 на осі Ox через x , а координату точки | N1 на | |||||||
| осі Oy через y. Числа | ( x , y ) | назвемо координатами точки | М на | ||||||
| площині ( x − абсциса, | y -ордината) .Це позначимо М ( x , y ) . | ||||||||
| Таким чином, система координат на площині встановлює | |||||||||
| взаємно однозначну відповідність між множиною всіх точок | |||||||||
| площини і множиною всіх упорядкованих пар дійсних чисел. |
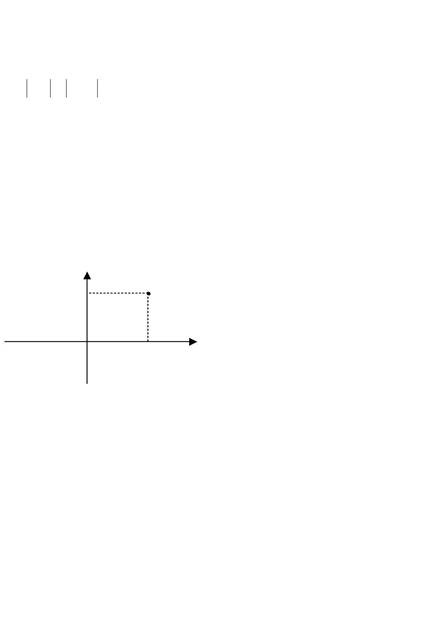
◙ Найпростіші задачі на застосування методу координат.
| а) Віддаль між двома точками на площині. | ||||||||||
| у | B | Нехай | задані | дві | точки | з | ||||
| своїми координатами: A( x1; y1) | , | |||||||||
| d | ||||||||||
| B2 | B( x2 ; y2 ) . | Треба знайти | віддаль | |||||||
| A2 | A | C | між цими точками. Зробимо малю- | |||||||
| х | нок (мал.6). | |||||||||
| A1 | B1 | Точки | A і B спроектуємо на | |||||||
| Мал.6 | ||||||||||
| координатні осі. Їх проекції на | ||||||||||
| вісьOx позначимо відповідно | через A1 і | B1 ,а | на вісь Oy | - | ||||||
| відповідно через A2 | і B2 . |
 Тоді ОA1 = x1,ОB1 = x2,ОA2 = y1,ОB2 = y2.
Тоді ОA1 = x1,ОB1 = x2,ОA2 = y1,ОB2 = y2.
Через точку A проведемо пряму, паралельну осі абсцис до пе-ретину з прямою BB1 в точці C . З одержаного прямокутного три-
кутника ABC за теоремою Піфагора знаходимо d 2 = AB 2 = AC 2 + BC 2 .






На основі формули (2.2) дану рівність перепишемо так:
| d 2 = | x2 − x1 | 2 + | y2 − y1 | 2 , абоd = ( x2 − x1)2 + ( y2 − y1)2 | (2.3) | |||||

Знак перед коренем у формулі (2.3) береться (+) тому, що віддаль – величина додатна.
Зауваження. Різниця координат у формулі(2.3)підноситьсядо квадрату і тому немає значення, яку точку вважати першою, а яку другою.
Приклад .Знайти віддаль між точкамиA( 4;5 )iB( 9;−7 ).Розв’язування. За формулою(2.3)знаходимо

d = ( 9 − 4 )2 + ( −7 − 5 )2 =  25 + 144 =
25 + 144 =  169 = 13.
169 = 13.
| у | B | б) Поділ відрізка в заданому | ||||
| відношенні. | ||||||
| B2 | y2 | |||||
| C2 | C | Нехай на площині задано дві | ||||
| y | довільні точки A(x1,y1) і B(x2,y2) | |||||
| A2 | y1 | A | Вважаємо A(x1,y1) першою точкою, | |||
| О | х1 | х | х2 | а B(x2,y2) другою точкою. Проведе- | ||
| A1 | C1 | B1х | мо через ці точки пряму(мал.7). | |||
| Мал.7 | Нехай точка С( x , y ) лежить |
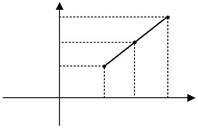
на відрізку AB і ділить його на два відрізки AC і CB , причому
відношення їх дорівнює λ , тобто λ = AC (число λ відоме). Випа-
 CB
CB
док, коли точка С співпадає з точкою B виключаємо, бо знаменник перетворюється в нуль. Наша задача полягає в тому, щоб знайти ко-ординати точки С( x , y ) через координати точок A( x1, y1) ,
B( x2 , y2 ). та числоλ.
Спроектуємо точки A,C та B на координатну вісь Ox (мал.7) і позначимо їх проекції через A1 , C1 та B1 . Використовуючи тео-рему про пропорційні відрізки, що містяться між паралельними
| прямими, | одержимо | A1C1 | = | AC | =λ . | Відомо, | що | ||||
| C1 B1 | |||||||||||
| CB | |||||||||||
| A1C1 = x − x1 , C1 B1 = x2 − x , тоді | x − x1 | =λ . | Розв’язуючи | цю | |||||||
| x2 − x | |||||||||||
| рівність відносно x , знаходимо | x = | x1 +λx2 | . | ||||||||
| 1 +λ |
Аналогічно, спроектувавши точки A,C та B на координатну вісь Oy (мал.7) і зробивши необхідні викладки, як вище, знаходимо
| ординату точки C : | y = | y1 +λy2 | . | |||||||||||||||
| 1 +λ | ||||||||||||||||||
| Отже, координати точки С( x , y ) , яка ділить відрізок AB | ||||||||||||||||||
| у відношенні | λ (рахуючи від A до B ), обчислюються за форму- | |||||||||||||||||
| лами | +λx | |||||||||||||||||
| = | x | |||||||||||||||||
| x | , | |||||||||||||||||
| 1 +λ | ||||||||||||||||||
| (2.4) | ||||||||||||||||||
| y | = | y1 +λy2 | . | |||||||||||||||
| 1 +λ | ||||||||||||||||||
| Якщо точка C є серединою відрізка AB , то λ = 1 і тоді | ||||||||||||||||||
| = | x | + x | ||||||||||||||||
| x | , | |||||||||||||||||
| (2.5) | ||||||||||||||||||
| y = | y1 + y2 | . | ||||||||||||||||
| Зауваження. При одержанні формул(2.4)ми допускали,що | ||||||||||||||||||
| відрізок | не паралельний ні | одній з | осей координат. Однак | |||||||||||||||
| АВ |
одержані формули (2.4) справедливі і тоді , коли відрізок АВ пара-лельний вісі Ox(y = y1 = y2), або осі Oy(x = x1 = x2) .

Крім цього, все викладене вище справедливе й тоді, коли точ-ка С( x , y ) знаходиться зовні АВ , тобто на його продовженні.

Приклад 1. Дано дві точкиA(7;-2)іB(-3;-5).На продовженніпрямої АВ знайти точку C(x,y), віддаль від якої до точки A в п’ять раз більша за віддаль до точки B. Знайти довжину AC .



| Розв’язування. Зробимо малюнок. | ||||||||||||||||||||||||||||||||||||||||||||
| За умовою | задачі | (мал.8) | у | |||||||||||||||||||||||||||||||||||||||||
| AC | ||||||||||||||||||||||||||||||||||||||||||||
| λ = | =−5. Тепер за формулою | |||||||||||||||||||||||||||||||||||||||||||
| CB | О | х | ||||||||||||||||||||||||||||||||||||||||||
| -3 | ||||||||||||||||||||||||||||||||||||||||||||
| (2.4) знаходимо | ||||||||||||||||||||||||||||||||||||||||||||
| -2 | A | |||||||||||||||||||||||||||||||||||||||||||
| 7 + ( −5 )( −3 ) | ||||||||||||||||||||||||||||||||||||||||||||
| x = | = | = − | , | |||||||||||||||||||||||||||||||||||||||||
| 1 + ( −5 ) | − 4 | |||||||||||||||||||||||||||||||||||||||||||
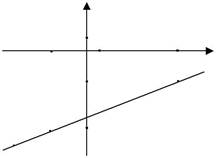 y = y =
| − 2 + ( −5 )( −5 ) | = | = − | . | B | -5 | ||||||||||||||||||||||||||||||||||||||
| C | ||||||||||||||||||||||||||||||||||||||||||||
| 1 + ( −5 ) | − 4 | Мал.8 | ||||||||||||||||||||||||||||||||||||||||||
| Значить, точка C( − | ;− | |||||||||||||||||||||||||||||||||||||||||||
| ) . | ||||||||||||||||||||||||||||||||||||||||||||
| Довжину | АС | знаходимо за формулою (2.3) | ||||||||||||||||||||||||||||||||||||||||||
| АС | = (7 + | )2 + ( −2 + | )2 = | 5 19 | . | |||||||||||||||||||||||||||||||||||||||
| Приклад | ||||||||||||||||||||||||||||||||||||||||||||
| 2. | Знаючи | координати | вершин | трикутника | ||||||||||||||||||||||||||||||||||||||||
| A( 2;3 ) , B( −4;5 ) і | C( −2;−5 ) , | знайти точку | M перетину медіан | |||||||||||||||||||||||||||||||||||||||||
| трикутника. | ||||||||||||||||||||||||||||||||||||||||||||
| Розв’язування. Координати точки D (середина сторони BC ) | ||||||||||||||||||||||||||||||||||||||||||||
| буде xD = − 4 − 2 = −3 , | yD | = | 5 − 5 | = 0 ,тобто D( −3;0 ) . | ||||||||||||||||||||||||||||||||||||||||
| Шукана | точка | M | ділить | кожну медіану у | відношенні | |||||||||||||||||||||||||||||||||||||||
 λ= 2 : 1 ,рахуючи від вершини.Тепер підставляючи у формули
λ= 2 : 1 ,рахуючи від вершини.Тепер підставляючи у формули
| (2.4) λ = 2 та координати | точок A і | D ,знайдемо координати | |||||||||||
| шуканої точки M . | |||||||||||||
| xM = | 2 + ( −3 )⋅ 2 | = | 2 − 6 | = − | ; yM | = | 3 + 0 ⋅ 2 | = | = 1. | ||||
| 1 + 2 | 1 + 2 | ||||||||||||
| Отже, | M ( − 4 ;1 ). | |||||||||
| §3. Декартова прямокутна система координат в просторі | ||||||||||
| Положення точки в просторі будемо визначати відносно | ||||||||||
| прямокутної | системи | координат | в | просторі. | Дана | система | ||||
| Оxyz складається із трьох взаємно перпендикулярних осей | Ox ,Oy | |||||||||
| та Oz , які перетинаються в одній точці O ,яка називається початком | ||||||||||
| координат. Вісь Ox називається віссю абсцис, вісь Oy - віссю орди- | ||||||||||
| z | нат і вісь Oz - віссю аплікат. | |||||||||
| Нехай точка M є довільною | ||||||||||
| C | ||||||||||
| M | точкою простору (мал.9). | |||||||||
| Знайдемо проекції точки | M | |||||||||
| B | на координатні осі. Для цього через | |||||||||
| точку | M проведемо три площини, | |||||||||
| y | ||||||||||
| x A | Мал.9 | які будуть перпендикулярні до ко- | ||||||||
| ординатних | осей | Ox ,Oy | та | |||||||
| Oz .Нехай ці площини перетинають вісі Ox ,Oy і | Oz відповідно в | |||||||||
| точках A,B і C . Тоді координата x точки A на осі Ox називається | ||||||||||
| абсцисою точки | M , | координата | y точки | B на | числовій | вісі | ||||
| Oy називається ординатою точки M , | а координата z точки C на | |||||||||
| числовій вісі Oz називається аплікатою точки | M .Значить, | величи- | ||||||||
| ни направлених відрізків ОА , ОВ та ОС , тобто числа x,y,z є коор- | ||||||||||
| динатами точки M. | ||||||||||
| Таким чином, в даній системі координат кожній точці | M | |||||||||
| простору відповідає єдина упорядкована трійка чисел (x; y; z ). В | ||||||||||
| цьому записі | x означає перше число, | y -друге, z -третє.І навпаки, | ||||||||
| кожній упорядкованій трійці чисел ( x; y; z ) відповідає тільки одна | ||||||||||
| точка простору M. Отже, прямокутна система координат в просторі | ||||||||||
| встановлює взаємно однозначну відповідність між множиною всіх | ||||||||||
| точок простору і множиною упорядкованих трійок чисел. | ||||||||||
| Площини Oxy, Oyz, і Oxz називаються координатними | ||||||||||
| площинами і поділяють весь простір на вісім частин. | ||||||||||
| Приклад 1.Побудувати точкиM1(1;–2;3), M2(–1;1;2). |
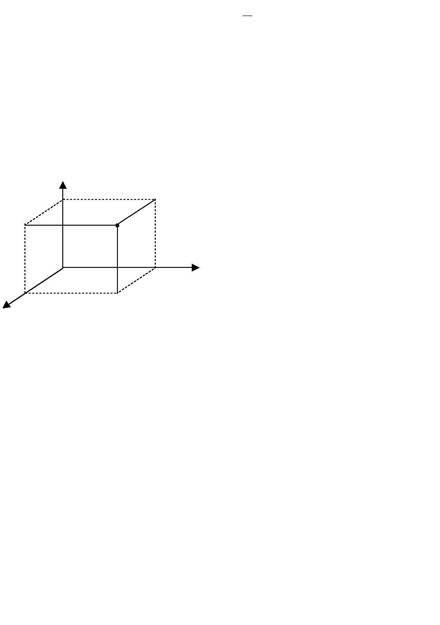
| Розв’язування. На вісі Ox відкладаємо відрізок OA = 1 .Через | ||||
| точку | A проводимо пряму, | z | ||
| паралельну вісі | Oy і на ній | |||
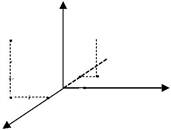
відкладаємо відрізок AB= -2. Через точку B проводимо пряму, паралельну вісі Oz і відкладаємо відрізок BM1=3
Кінець цього відрізка дає шука-ну точку M1 (мал.10). Точка M2(-1;1;2) будується аналогічно.
М1 
 M2
M2
| A | 01 | 1 | y |
| B |
x Мал.10
§ 4. Скалярні і векторні величини
У фізиці, математиці, економіці і інших науках зустрічаються величини двох видів: одні з них характеризуються тільки числом, а інші – числом і напрямом в просторі.
Величини називаються скалярними або скалярами, якщо кож-на із них визначається своїм числовим значенням у вибраній системі одиниць, наприклад, довжина, площа, об’єм, час, температура.
Величини називаються векторними або векторами, якщо кож-на із них визначається числовим значенням і напрямом. Наприклад, сила, швидкість, прискорення.
Означення. Напрямлений відрізок прямої називається век-
Тором.
→
Вектор будемо позначати символом AB . Перша буква означає по-чаток вектора, а друга – його кінець. Вектор також будемо познача-
→ ти однією малою буквою з стрілкою на
| a | → | |
| А | В | верху, наприклад a (мал.11). |
| Мал.11 | Якщо початок і кінець вектора | |
| → |
 співпадають, то вектор називається нульовим і позначається 0 або просто 0 .Віддаль між початком і кінцем вектора називається його
співпадають, то вектор називається нульовим і позначається 0 або просто 0 .Віддаль між початком і кінцем вектора називається його
→
довжиною , або модулем і позначається AB або а .




Ми будемо вивчати вільні вектори. Такий вектор можна пере-носити по його лінії дії або паралельно самому собі.
Означення. Вектори, які знаходяться на паралельних пря-мих, або на одній і тій же прямій, називаються колінеарними.
Означення. Вектори, які знаходяться на паралельних площи-нах або на одній і тій же площині, називаються компланарними.
Відповідно, компланарні вектори, які приведені до одного і того ж початку, будуть знаходитися на одній площині.
Означення. Два вектори рівні, якщо вони однаково напрямлені і модулі їх рівні .
Означення. Два вектори, в яких модулі рівні, а напрямки
| → | → | |||||||||||||||||||||||||
| протилежні, називаються протилежними a і ( − a ). | ||||||||||||||||||||||||||
| → | → | |||||||||||||||||||||||||
| Одиничний вектор (орт) | вектора | дорівнює | a | і | ||||||||||||||||||||||
| a | ||||||||||||||||||||||||||
| → | ||||||||||||||||||||||||||
| → | → | а | ||||||||||||||||||||||||
| позначається так: | = | a | ||||||||||||||||||||||||
| a | . | |||||||||||||||||||||||||
| → | ||||||||||||||||||||||||||
| §5.Дії над | а | |||||||||||||||||||||||||
| векторами |
Читайте також:
- D) методу мозкового штурму.
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I Метод Шеннона-Фано
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. Метод рiвних вiдрiзкiв.
- V. Виконання вправ на застосування узагальнювальних правил.
- VII. Нахождение общего решения методом характеристик
- А. науковий факт, b. гіпотеза, с. метод
- А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Автомобільні ваги із застосуванням цифрових датчиків
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розділ 2. АНАЛІТИЧНА ГЕОМЕТРІЯ І ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ | | | Співпадає з початком вектора |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |