Основні поняття про функції багатьох змінних

Вивчення зв’язків і закономірностей, які існують в матеріаль-ному світі, часто приводять до функції не однієї, а багатьох змінних. Ці функції дозволяють виражати більш складні залежності, ніж фу-нкції однієї змінної. Тому теорія функцій багатьох змінних має ши-роке практичне застосування в різних галузях.

1.1. Означення функції багатьох змінних.

Функція двох змінних та її графічне зображення

Змінні x₁, x₂,..., x_n називаються незалежними між собою, як-

що кожна із них може приймати довільні значення в своїй області зміни незалежно від того, які значення приймають при цьому інші змінні.

Означення1. Функцією багатьох змінних u = f ( x₁ ,x₂	,...,x_n )
називається така закономірність,	при якій змінним x₁ , x₂	,..., x_n
із деякої множини	D ⊂ Rⁿ ставиться у відповідність одне зна-
чення u із множини E ⊂ R′ .
Наприклад:	z = x² + y² ,	z =	xy , u = x² + y² + z² .
Множина D називається областю визначення функції
u = f ( x₁ ,..., x_n ), а множина E -	область значень цієї функції. На-
приклад, функція z =	9 − x² − y²	задана для всіх x і y , для яких

виконується нерівність x² + y² ≤ 9. У даному випадку областю ви-

значення функції є круг на площині x0 y з центром в точці O( 0;0 ) і радіу-

сом R=3 Область значень цієї функції

E =[0 ;3].

Частинним випадком функції ба-гатьох змінних є функція двох змінних z = f ( x , y ), для якої можна дати по-

няття графіка функції. В загальному випадку графіком такої функції є пове-рхня у трьохвимірному просторі R³

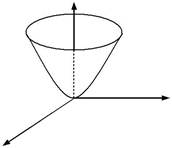
_O y

Мал.1

Приклад 1. z=x²+y² .Графіком цієї функції є параболоїдобертання (мал.1).

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Еластичністю пропозиції відносно ціни називається гра-ниця відношення відносного приросту пропозиції до відносного приросту ціни при умові, що приріст ціни прямує до нуля.	\|	Економічні задачі, що приводять до поняття функцій багатьох змінних

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.014 сек.