• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Коефіцієнт кореляції Пірсона

Коефіцієнт кореляції Пірсона r, який є безрозмірним індексом в інтервалі від – 1,0 до 1,0 включно, відображає міру лінійної залежності між двома множинами даних.

Показник тісноти зв'язку між двома ознаками визначається по формулі лінійного коефіцієнта кореляції:

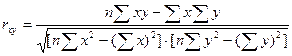
де x – значення факторної ознаки;

y – значення результативної ознаки;

n – число пар даних.

Парна кореляція – це зв'язок між двома ознаками: результативним і факторним або двома факторними.

Варіанти зв'язку, характеризує наявність або відсутність лінійного зв'язку між ознаками:

Ø великі значення з одного набору даних пов'язані з великими значеннями іншого набору (позитивна кореляція) – наявність прямого лінійного зв'язку;

Ø малі значення одного набору пов'язані з великими значеннями іншого (негативна кореляція) – наявність негативного лінійного зв'язку;

Ø дані двох діапазонів ніяк не зв'язані (нульова кореляція) – відсутність лінійного зв'язку.

Як приклад візьмемо набір даних А (таблиця 8.1). Необхідно визначити наявність лінійного зв'язку між ознаками x і y.

Для графічного представлення зв'язку два змінних використана система координат з осями, відповідними змінним x і y. Побудований графік, названий діаграмою розсіювання, показаний на рис. 8.2. Дана діаграма показує, що низькі значення змінної x відповідають низьким значенням змінної y, високі значення змінної x відповідають високим значенням змінної y. Цей приклад демонструє наявність явного зв'язку.

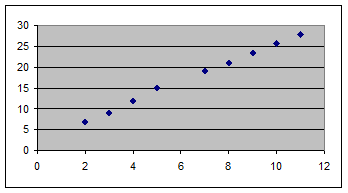
Рис. 8.2. Діаграма розсіювання

Таким чином, ми можемо встановити залежність між змінними x і y. Розрахуємо коефіцієнт кореляції Пірсона між двома масивами (x і y) за допомогою функції MS Excel ПИРСОН(массив1;массив2). В результаті отримаємо значення коефіцієнта кореляції, що дорівнює 0,998364, тобто зв'язок між змінними x і y є дуже високим. Використовуючи пакет аналізу MS Excel і інструмент аналізу "Корреляция", можемо побудувати кореляційну матрицю.

Будь-яка залежність між змінними володіє двома важливими властивостями: величиною і надійністю. Чим сильніше залежність між двома змінними, тим більше величина залежності і тим легко передбачити значення однієї змінної за значенням іншої змінної. Величину залежності легко виміряти, чим надійність.

Надійність залежності не менш важлива, чим її величина. Ця властивість пов'язана з показністю досліджуваної вибірки. Надійність залежності характеризує, наскільки імовірно, що ця залежність буде знову знайдена на інших даних.

Із зростанням величини залежності змінних її надійність зазвичай зростає.

Читайте також:

1. А середній коефіцієнт росту в такому випадку визначається як
2. А. Фінансові коефіцієнти
3. А. Фінансові коефіцієнти
4. Аналіз коефіцієнтів цільової функції
5. Аналіз фінансових коефіцієнтів.
6. Безрозмірною характеристикою гідротрансформатора називається залежність коефіцієнтів пропорційності моментів насосного і турбінного коліс від його передаточного відношення.
7. Біноміальні коефіцієнти
8. Визначення коефіцієнта оборотності активів
9. Визначення коефіцієнта чистого прибутку
10. Визначення коефіцієнтів рівнянь лінійної регресії для багатофакторної задачі
11. Визначення коефіцієнтів чотириполюсника за дослідами неробочого ходу та короткого замикання.
12. Визначення коефіцієнтів чотириполюсника за матрицею власних та взаємних опорів методу контурних струмів.

Переглядів: 10432