Модель доказу програми за твердженнями

Розглядається формальний доказ програми, заданої структурною логічною схемою і сукупністю тверджень, що задаються логічними операторами, комбінаціями змінних (true/false), операціями (кон’юнкція, диз'юнкція й ін.) і кванторами загальності й існування (табл.1).

Таблиця 3.1. Список логічних операцій

Логичні операції
Назва	Приклад	Значення
Кон’юнкція	x & y	x і y
Диз’юнкція	x y*	x або y
Заперечення	Øx	ні x
Імплікація	x ® y	якщо х то у
Еквівалентність	х = у	Х рівнозначно у
Квантор загальності	" х Р(х)	для всіх х, умова істинно
Квантор існування	$ х Р(х)	Існує х, для якого Р(х) істина

Ціль алгоритму програми – побудова для масиву цілих чисел Т довжини N (array Т[1:N])еквівалентного масиву Т’ тієї ж довжини N, що і масив Т. Елементи в масиві Т’ повинні розташовуватися в порядку зростання їхніх значень. Даний алгоритм реалізується сортуванням елементів вихідного масиву Т по їхньому зростанню. Доказ правильності алгоритму сортування елементів масиву Т проводиться з використанням ряду тверджень щодо елементів цього алгоритму, якій описуються пунктами П1– П6.

П1. Вхідна умова алгоритму задається у вигляді початкового твердження:

А_beg: (Т [1:N]– масив цілих) & ( Т' [1:N] масив цілих ).

Вихідне твердження А_end – це кон’юнкція таких умов:

(а) (Т– масив цілих ) & (Т' – масив цілих)

(б) ("i , якщо i £ N, те $ j (T'( i ) £ T' ( j ))),

(в) (" i , якщо i < N, те (T' ( i ) £ T' ( i+1)),

Тобто А_end – це (Т – масив цілих ) & (Т' – масив цілих)

& "i, якщо i £ N, те$ j (T'( i ) £ T' ( j )),

& "i , якщо i < N, те(T' ( i ) £ T' ( i+1) ).

Розташування елементів масиву Т в порядку зростання їхніх величин у масиві Т’ здійснюється алгоритмом пузиркового сортування, суть якого полягає в попереднім копіюванні масив Т в масив Т', а потім проводиться сортування елементів згідно умови їхнього зростання. Алгоритм сортування представлено на рис.3.5.

Оператори алгоритму розміщені в прямокутниках, умови вибору альтернативних шляхів – паралелограмами, крапки з початковим A_beg і кінцевим A_endумовами і станами алгоритму – кружками.

У кружках також задано: початковий стан – 0, стан після обміну місцями двох сусідніх елементів у масиві Т' – одна зірочка, стан після обміну місцями всіх пар за один прохід усього масиву Т' – дві зірочки.

Крім уже відомих змінних Т, T' і N, в алгоритмі використані ще дві змінні: i – типу ціла і М – булева змінна, значенням якої є логічні константи true і false.

П2. Для доказу того, що алгоритм дійсно забезпечує виконання вихідних умов, розглянемо динаміку їхнього виконання послідовно у визначених точках алгоритму.

Помітимо, що точки поділяють алгоритм на відповідні частини, правильність кожної з них улаштовується окремо.

Так оператор присвоювання означає, що для всіх i (i £ N & i>0) виконується (T' [i] : = T [i]).Результат виконання алгоритму в точці з нулем може бути виражений твердженням (T[1: N]– масив цілих) & (T '[1: N] – масив цілих)

& ("i якщо i £ N (T [ i] = T [ i] )).

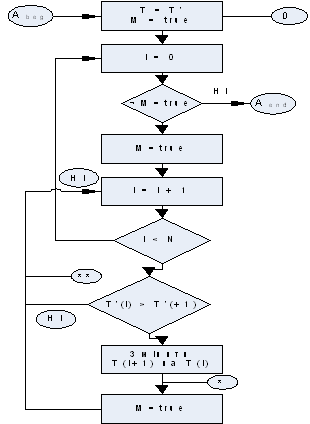
Рис.3.5. Схема сортування елементів масиву Т'

Доказ очевидно, оскільки за семантикою оператора присвоювання (поелементне пересилання чисел з Т в T’) самі елементи при цьому не змінюються, до того ж у даній точці їхній порядок у Т и T' однаковий. Отже одержали, що виконується умова б) вихідного твердження.

Помітимо, що перший рядок доведеного твердження збігається з умовою а) вихідного твердження А_end і залишається справедливим до кінця роботи алгоритму, тому в наступних твердженнях приводитися не буде.

У точці з одною зірочкою виконаний оператор

(i < N)(T'(i)) > T' (i + 1) ® (T' (i) і T'(i + 1), що змінює місцями елементи.

У результаті роботи оператора буде справедливим таке твердження:

$ i, якщо i < N, те(T'(i) < T'(i +1),

яке є частиною умови в) твердження А_end (для однієї конкретної пари суміжних елементів масиву T'). Очевидно також, що семантика оператора обміну місцями не порушує умову б) вихідного твердження А_end.

У точці з двома зірочками виконані всі можливі обміни місцями пари суміжних елементів масиву T' за один прохід через T', тобто оператор обміну працював один або більше раз. Однак позиркові сортування не дає гарантії, що досягнуто упорядкування за один прохід по масиву T', оскільки після чергового обміну індекс i збільшується на одиницю незалежно від того, як співвідноситься новий елемент T'(i) з елементом T'(i – 1).

У цій точці також справедливе твердження

$i, якщо i < N, те T'( i) < T' ( i + 1).

Частина алгоритму, позначена точкою з двома зірочками, виконується доти, поки не буде упорядкований весь масив, тобто не буде виконуватися умова в) твердження А_еnd для всіх елементів масиву T':

"i, якщо i < N, те T' (i) < T' (i+ 1).

Отже, виконання вихідних умов забезпечено порядком і відповідною семантикою операторів перетворення масиву.

Доведено, що виконання алгоритму програми завершено успішно, що означає її правильність.

П3. Цей алгоритм можна представити у вигляді серії теорем, що доводяться. Починаючи з першого твердження і переходячи від одного перетворення до іншого, визначається індуктивний шлях висновку. Якщо одне твердження – правильно, то істинно й інше. Іншими словами, якщо дано перше твердження А₁і перша точка перетворення А_2, те перша теорема – А₁® А₂.

Якщо А₃ – наступна точка перетворення, то другою теоремою буде А₂ ® А₃.

Таким чином формулюється загальна теорема А_і ® А_j, де А_і й А_j – суміжні точки перетворення. Ця теорема формулюється так, що якщо умова істинна в останній точці, то істинно і вихідне твердження А_k ® А_end.

Отже можна повернутися до точки перетворення А_end і до попередньої точки перетворення. Довівши, що А_k ® А_end вірно, виходить, вірно й А_j® А_j+₁і так далі, поки не одержимо, що А₁® А_0.

П4. Далі специфікується твердження типу if – then.

П5. Щоб довести, що програма коректна, необхідно послідовно розташувати усі твердження, починаючи з А₁ і закінчуючи А_end, цим підтверджується істинність вхідної і вихідної умов.

П6. Доказ алгоритму програми завершено.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Методи доведення правильності програм	\|	З.5. Проектування ПС засобами ЖЦ з реалізації доменів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.002 сек.