
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Лексикографічний метод генерації перестановок
Досить часто приходиться розв’язувати задачі з використанням знань з комбінаторики – досить цікавого розділу з математики. Для прикладу розглянемо таку задачу.
Задача 195. Скільки різних “слів” можна утворити з слова “ПЕОМ”. Літери дозволяється використовувати стільки разів, скільки вони є у даному слові. Вивести всі слова на екран.
Розв’язання: Якби в умові задачі не ставилась вимога вивести всі слова на екран, то це була б чисто комбінаторна задача, яка розв’язувалась би досить просто: оскільки всі літери в слові різні, то нам просто потрібно знайти кількість розміщень у множині, що складається з чотирьох елементів. З іншими способами розв’язання задач з використанням множин ми познайомимось трохи пізніше у відповідному розділі. Зараз лише нагадаємо, що якщо дано множину А з n елементів а1, а2, ..., аn-1, an, то розміщенням з n елементів по m (m Ј n) називається будь–яка впорядкована підмножина В множини А, така, що вона містить m елементів із даних а1, а2, ..., аn–1, аn. Причому дві такі підмножини вважаються різними, якщо вони відрізняються порядком або складом елементів.
Будемо поки що розглядати не множину літер слова «ПЕОМ», а множину порядкових номерів літер у цьому слові. Оскільки слово «ПЕОМ» складається з чотирьох літер, то ми маємо множину з чотирьох елементів: 1, 2, 3, 4. Розміщень по одному буде 4: (1); (2); (3); (4); Розміщень по два – дванадцять: (1, 2); (2, 1); (1, 3); (3, 1); (1, 4); (4, 1); (2, 3); (3, 2); (2, 4); (4, 2); (3, 4); (4, 3). Згадаймо, що у нас числа моделюють літери слова, а у слові всі літери різні (бо мають різний порядковий номер!) і не можуть повторюватись. У загальному випадку кількість розміщень з n елементів по m – 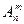 знаходиться за формулою:
знаходиться за формулою:

але з точки зору інформатики нам зручніше використовувати ту ж формулу, але записану у вигляді: 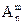 =n Ч (n-1) Ч (n-2) Ч ... Ч (n-(m-2)) Ч (n-(m-1)). Зручність використання полягає в тому, що у циклах нам зручніше працювати з цілочисельними змінними, а операція ділення вимагає використання дійсних типів. Використавши формулу, маємо:
=n Ч (n-1) Ч (n-2) Ч ... Ч (n-(m-2)) Ч (n-(m-1)). Зручність використання полягає в тому, що у циклах нам зручніше працювати з цілочисельними змінними, а операція ділення вимагає використання дійсних типів. Використавши формулу, маємо: 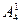 =4,
=4, 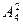 = 12,
= 12,  = 24,
= 24,  = 24. Всього ми можемо утворити
= 24. Всього ми можемо утворити 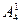 +
+ 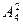 +
+  +
+  = 64. Тобто з точки зору інформатики задача поки що мало цікава, але ось вирішення питання виведення всіх варіантів новоутворених слів на екран робить подальший розв’язок цієї задачі самостійним методом для розв’язання великої групи завдань.
= 64. Тобто з точки зору інформатики задача поки що мало цікава, але ось вирішення питання виведення всіх варіантів новоутворених слів на екран робить подальший розв’язок цієї задачі самостійним методом для розв’язання великої групи завдань.
Нам потрібно навчитись утворювати нові слова з заданого набору літер. Розіб’ємо це завдання на дві підзадачі.
Підзадача 1: Спочатку навчимось утворювати слова з набору з n літер, причому кількість літер у слові повинна становити також n (у термінах інформатики задачу можна сформулювати так: скласти програму для отримання всіх перестановок з n літер). Утворювати слова нам допоможуть їх порядкові номера. Оскільки множина порядкових номерів літерів слова на початку є впорядкованою за зростанням: 1, 2, 3, 4, то будемо діяти згідно алгоритму генерації перестановок лексикографічним методом наступним чином:
n вивести на друк введено слово;
n починаючи з кінця слова шукаємо перший елемент, який менший за попередній (рахуючи з кінця) і відмічаємо його;
n знову починаємо з кінця і шукаємо ще один елемент, але вже більший за відмічений, причому він повинен бути розміщеним до відміченого, рахуючи з кінця;
n якщо другий елемент знайдено, то міняємо його місцями з першим;
n “хвіст”, що утворився після обміну (після номера елемента, знайденого першим) сортуємо в порядку зростання. Оскільки до цього він був впорядкований в порядку спадання то у даному випадку операція сортування зводиться до обміну місцями відповідних елементів “хвоста”, або іншими словами – “хвіст” потрібно записати навпаки;
n все вищесказане виконуємо до тих пір, доки весь масив не буде впорядковано в порядку спадання.
Все вищесказане і являє собою алгоритм генерації всіх перестановок лексикографічним методом, але ми описали алгоритм генерації перестановок натуральних чисел. Для використання даного алгоритму стосовно до генерації всіх можливих “слів” з заданого слова поступимо досить просто. Будемо генерувати перестановки для натуральних чисел, що є номерами місцезнаходження літер у введеному слові, тобто індексами введеного масиву символів.
Тобто ми вже зараз можемо утворити всі “чотирилітерні” слова з слова ПЕОМ, більше того даний алгоритм дає нам змогу знаходити всі n–літерні слова з введеного довільного введеного n–літерного слова. На даному етапі програма утворення всіх можливих n–літерних слів матиме вигляд:
program perestanovki_leksikografika;
uses dos,crt;
var st, st1 : string; { для слів }
i, k,n,t,j,m : integer; { для циклів і проміжних змінних }
n : integer; { кількість символів в рядку }
mas : array[1..10] of integer; { масив № символів в заданому слові }
begin
write(‘Введіть слово: ’);
readln(st);
{ .......... формування початкового масиву з номерів символів .......... }
n := length(st); { кількість символів в слові }
for i:=1 to n do mas[i]:=i; { заповнюємо масив номерами літер }
k:=1; { припускаємо, що існує хоча б 1 перестановка }
while k<>0 do { доки існує хоча б 1 перестановка діє }
begin { алгоритм формування нової перестановки, а пока що }
st1:=''; { приготувались до утворення нового слова }
for j:=1 to n do st1:=st1+st[mas[j]]; { утворили нове слово }
write(st1:8); { надрукували нове слово }
j:=n; { Алгоритм: починаючи з кінця масиву № літер }
k:=0; { і вважаючи, що більше перестановок нема }
while (k=0) and (j>1) do { доки не знайшли перестановку і не }
begin { досягли початку масиву }
if mas[j-1]<mas[j] then k:=j-1; { шукаємо перший елемент, }
j:=j-1; { менший за попередній, рахуючи з кінця }
end; { якщо не знайдемо, то k = 0 і все перестановки знайдено }
j:=n; { переходимо до пошук другого елементу }
t:=0; { і припускаємо, що його не існує }
while (t=0) and (j>k) do { доки не визначили положення другого і
не досягли положення першого – шукаємо другий елемент, який }
begin
if mas[j]>mas[k] then t:=j; { більший першого відміченого, }
dec(j); { причому також ідемо з кінця і до }
end; { першого відміченого. }
if t>0 then begin { Другий знайдено – міняємо його місцями з першим }
j:=mas[k];
mas[k]:=mas[t];
mas[t]:=j;
end;
m:=1; { відсортуємо «хвіст» в порядку спадання – шикуємо навпаки }
while m < (n-k+1) / 2 do
begin
i := mas[k+m];
mas[k+m] := mas[n+1-m];
mas[n+1-m] := i;
m := m+1;
end;
readln; { для візуального контролю дій алгоритму }
end; { кінець алгоритму генерації всіх перестановок }
readln; { для візуального контролю кінця алгоритму }
end.
Дана програма прекрасно утворює всі можливі n–літерні слова, але за однієї умови: всі літери в слові повинні бути різні. А як нам бути у випадку, коли у слові є однакові літери? Наприклад, «мама». Позначимо для наочності першу з однакових літер «а», а другу – «А». Тоді слова «мамА» і «мАма», що утворені літерами з різними порядковими номерами в дійсності записані одними й тими ж літерами і є однаковими, хоча і відповідають різним числовим перестановкам «1234» та «1432».
У цьому випадку потрібно до запропонованого алгоритму внести невеличке доповнення, яке полягає в тому, що на етапі формування початкового масиву номерів літер однаковим літерам слід присвоювати однакові номера. Подумайте, як це зручно зробити і самостійно модифікуйте дану програму.
Нам залишилось розібрати другу підзадачу, яку ми сформулювали для повного вирішення поставленої задачі: потрібно згенерувати всі можливі 1–4–літерні «слова» (ми ж поки що сформували лише всі 4–літерні слова). Розв'язання другої підзадачі ми перекладаємо на читача, оскільки вважаємо, що він вже до цього підготовлений.
Читайте також:
- D) методу мозкового штурму.
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I Метод Шеннона-Фано
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. Метод рiвних вiдрiзкiв.
- VII. Нахождение общего решения методом характеристик
- А. науковий факт, b. гіпотеза, с. метод
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
- Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
- АгротехнІЧНИЙ метод
- Адаптовані й специфічні методи дослідження у журналістикознавстві
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклади розв’язування задач з використанням основних операцій для роботи з літерними величинами | | | Вправи та завдання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |