• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ІІІ. Метод Лагранжа

Лагранж запропонував загальний метод розв’язування неоднорідних лінійних ДР. Спочатку розв’язується однорідне ДР. У загальний розв’язок входять довільні сталі. Потім шукається загальний розв’язок неоднорідного ДР і при цьому довільні сталі стають новими шуканими функціями.

Шукатимемо розв’язок неоднорідного ДР (13).

Спочатку розв’яжемо однорідне ДР 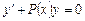. Загальний розв’язок має вигляд 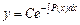. Шукаємо розв’язок неоднорід­ного ДР у вигляді 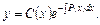Підставляючи в ДР ( ), дістаємо рівняння

.

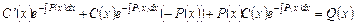Приходимо до простого ДР

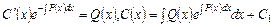
і загального розв’язку неоднорідного ДР виду (14):

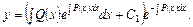
Метод Лагранжа часто називають методом варіації довільної сталої.

Приклад. Знайдемо за методом Лагранжа розв’язок неоднорід­ного лінійного ДР

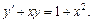
l Спочатку знайдемо загальний розв’язок однорідного ДР: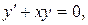

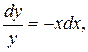
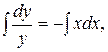
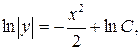
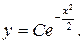
Шукаємо розв’язок неоднорідного ДР у вигляді .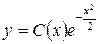

Підставивши в неоднорідне ДР, дістанем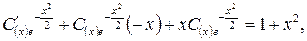о або

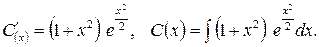
Використаємо формулу інтегрування частинами:

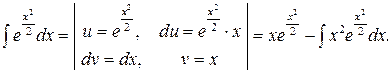
Отже, остаточно дістанемо загальний розв’язок ДР:

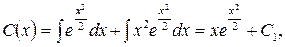
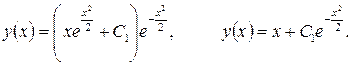
До лінійного ДР зводиться ДР Бернуллі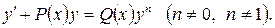

Вводиться нова змінна , і ДР для z набирає вигляду ДР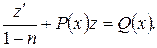

Пониження порядку деяких диференціальних рівнянь другого порядку

У загальному випадку ДР другого порядку має вигляд

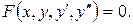
Загальний розв’язок рівняння містить дві довільні сталі: 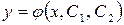(16)

і за рахунок вибору довільних сталих 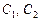можна розв’язати задачу Коші, яка полягає в пошуку частинного розв’язку , що задовольняє початкові умови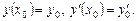

Для ДР другого порядку частіше зустрічається на практиці крайова задача, коли умова на шуканий розв’язок 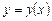задається при різних значеннях аргументу.

У деяких випадках можна знизити порядок ДР другого порядку (15) і звести до ДР першого порядку.

І. У ДР відсутня шукана функція. ДР виду

(17)

зводяться до ДР першого порядку, якщо візьмемо 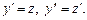Дістанемо ДР першого порядку

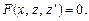(18)

Якщо буде знайдено загальний розв’язок цього рівняння 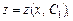то дістанемо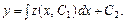

Якщо ДР другого порядку має вигляд то беремо 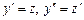і дістаємо ДР першого порядку 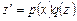з відокремлюваними змінними:

Читайте також:

1. D) методу мозкового штурму.
2. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
3. I Метод Шеннона-Фано
4. I. Метод рiвних вiдрiзкiв.
5. VII. Нахождение общего решения методом характеристик
6. А. науковий факт, b. гіпотеза, с. метод
7. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
8. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
9. АгротехнІЧНИЙ метод
10. Адаптовані й специфічні методи дослідження у журналістикознавстві
11. Адміністративні (прямі) методи регулювання.
12. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.

Переглядів: 2410