• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення вектора за компонентами

Розглянутий спосіб описання вектора грунтується на наочності і узагальненню на випадок n-вимірного простору не піддається. Тому розглянемо інший спосіб описання вектора. Візьмемо тривимірний простір XYZ. Нехай у ньому задано вектор = 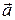. Через початок і кінець цього вектора проведемо пло­щини, паралельні координатним площинам. Координати точок пере­тину цих площин з координатними осями позначимо відповідно x_1, y₁, z₁, x_2, y₂, z₂ (рис. 2.3).

Початок і кінець вектора = 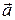містяться в точках А (x_1, y₁, z₁) і В (x_2, y₂, z₂) Різниці x₁ – x₂, y₁ –y₂ , z₁-z₂ називають компонентами (координатамиабо проекціями на координа­тні осі)вектора = `.

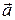Вектор АВ однозначно визначається упорядкованою трійкою чисел a_х = x₁ – x₂ a_у = y₁ –y₂ a_z =z₁-z₂ або компонентами. Записують це так:

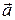=( a_х, a_у, a_z)

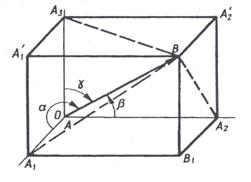
Рис. 2.3 Рис. 2.4

Справді, побудуємо на як на діагоналі, прямокутний пара­лелепіпед АА₁В₁А₂А₂’ВА₁’A₃ (рис. 2.4) із сторонами AA₁ = x₂–x₁; AA₂=y₂-y₁; AA₃=z₂-z₁ Із прямокутних трикутників АА₁В, АА₂В, АА₃В знаходимо

a_x=x₂-x₁=|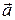|cos

a_y=y₂-y₁=|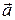|cos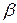

a_z=z₂-z₁=|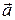|cos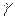

Оскільки при паралельному переносі вектора його довжина і ку­ти не змінюються, то два рівних між собою вектори завжди мають одні і ті самі компоненти.

Два вектори рівні між собою тоді і тільки тоді, коли рівні між собою їхні відповідні компоненти.

Якщо початок вектора збігається з початком координат, то вектор називається радіусом-вектором точкиВ і його компо­ненти збігаються з координатами його кінця — точки В.

Розглянемо n-вимірний простір. Будь-яка упорядкована пара то­чок А і В n-вимірного простору називається n-вимірним векто­ром.Одна з цих точок називається початком,друга — кінцем вектора.Упорядкованій парі точок А і В з координатами А (х₁, х₂, x₃,… х_n) і В (у₁, у₂, уз,… у_n) відповідає упорядкована сукупність різниць а₁ = у₁ – х₁;а₂ = у₂- х₂; а_з=у₃ - х₃;… а_n = у_n- х_n, які називають компонентами вектора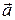і пишуть 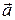= (а₁, a₂, a_3,… а_n). Таким чином, компоненти n-вимірного вектора — це упорядкований набір дійсних чисел. Тому n-вимірний вектор можна визначити як довільний упорядкований набір (a₁, а₂, а₃,…а_n) дійсних чисел у вибраній системі координат.

Вектор, всі компоненти якого дорівнюють нулю, називається нуль-вектором.Два n-вимірні вектори 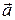= (a₁, a₂, a_3,… а_n) і = (b₁, b₂, b_3,… b_n) вважаються рівними між собою, якщо рівні між собою їхні відповідні компоненти, тобто

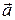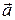=, якщо a₁ = b₁; а₂=b₂;…а_n = b_n; = (а₁, a₂, a_3,… а_n)=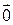, якщо a₁=0, a₂=0,…a_n=0

Афінний простір називається векторним простором,якщо в ньому введено поняття вектора так, що:

1) будь-якій парі точок А і В відповідає єдиний вектор;

2) для будь-якої точки А афінного простору і будь-якого вектора 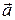існує єдина точка В така, що =;

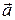3) для будь-яких трьох точок A, В і С справджується рівність + = .

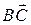Компоненти n-вимірного вектора можна розміщувати у рядок або у стовпчик. У першому випадку говорять про вектор-рядок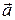= (а₁, a₂, a_3,… а_n), а у другому — про вектор-стовпець.Вектор-рядок або вектор-стовпець називають ще матрицею-рядкомабо матрицею- стовпцемі позначають так:

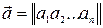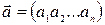, або , або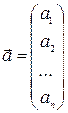

Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Алгебраїчний спосіб визначення точки беззбитковості
6. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
7. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
8. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
9. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.
10. Безстатеве розмноження, його визначення та загальна характеристика. Спори — клітини безстатевого розмноження, способи утворення і типи спор.
11. Біостратиграфічні методи визначення віку порід
12. Біуретовий метод визначення білків

Переглядів: 1809