• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задача розподілу ресурсів

Важливий клас економічних задач утворюють процеси розподілу, обумовлені завжди обмеженістю ресурсів і засобів, необхідних для функціонування певної системи. Зміст задачі полягає в пошуку такого плану розподілу ресурсів, який би забезпечував результат, оптимальний за певним критерієм якості.

Розглянемо в загальному вигляді задачу багатоетапного розподілу ресурсів, та подамо алгоритм її розв’язування.

Нехай в наявності є деяка кількість засобів , які потрібно вкласти в

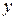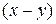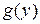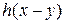розвиток двох неоднорідних підприємств. Відомо, що якщо в перше підприємство вкласти , а в друге – засобів, то прибуток, відповідно, буде становити і . Необхідно так вибрати величину у (розподілити засоби між підприємствами), щоб загальний прибуток 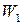був максимальним, тобто значення функції 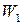стало максимальним

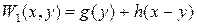(5.2)

Якщо функції g і h неперервні при всіх значеннях у, тоді максимальне значення функції 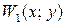завжди існує і визначає величину можливого максимального прибутку в однокроковому процесі. Необхідно зауважити також, що одиниці вимірювання прибутків можуть відрізнятися від одиниць вимірювання засобів .

Розглянемо тепер двоетапний процес. Припустимо, що за рахунок витрат, необхідних для отримання прибутку 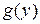, початкова кількість засобів у зменшується до величини ау, де а- деяка стала (0 < а < 1), а початкова кількість засобів (х-у)до величини за рахунок витрат, що дають прибуток h(x-y). Таким чином, після здійснення одноетапного процесу залишок засобів буде складати х₁= 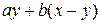. На другому етапі вибираємо 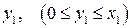так, щоб функція

,

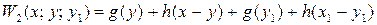як функція двох змінних у і 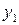приймала найбільше значення.

В 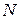-етапному процесі, в якому процедура розподілу проводиться послідовно N разів, повний прибуток визначається функцією

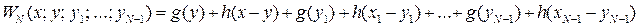(5.3),

де величини , які підлягають подальшому розподілу після першого, другого, ..., ( 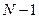)-го етапів, визначаються наступними співвідношеннями:

……………........................................
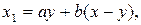
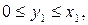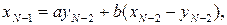
(5.4)

Максимальний сумарний прибуток отримується при тих значеннях змінних, при яких функція (5.3) як функція 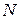змінних приймає найбільше значення, і які задовольняють системі обмежень (5.4). Їх знаходження зв'язане з великими труднощами, тому здійснимо його поетапно, дотримуючись принципу оптимальності в 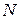-етапному процесі. Зауважимо, що максимальне значення повного прибутку в N-етапному процесі залежить тількивід 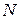і величини х. Тому визначимо функцію як максимум прибутку, отриманого від 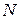-етапного процесу, який починається з величини , для і х >0, тобто

.

Для одноетапного процесу отримаємо функціональне рівняння

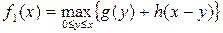. (5.5)

Розглядаючи двохетапний процес, зауважимо, що повний прибуток складається із прибутків від першого і другого етапів, на яких розподілу підлягає 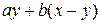одиниць ресурсу. Значить, якщо 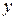вибрали оптимально, то на другому етапі отримаємо прибуток 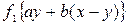, а повний прибуток від двохетапного процесу виразиться рекурентним співвідношенням

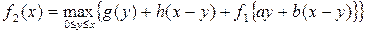. (5.6)

Міркуючи аналогічно, для N-етапного процесу отримаємо основне функціональне рівняння

,(5.7)

де N>2. Використовуючи функцію 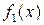(5.5) за формулою (5.7), обчислюємо 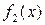, , 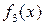... , 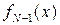. При цьому на кожному етапі обчислення отримуємо не тільки 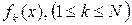, але й , оскільки розподіл вихідних ресурсів х був оптимальним.

Застосування описаного вище методу до розв'язування задач ДП дозволяє звести одну 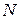- вимірну задачу до послідовності N одновимірних задач.

Припустимо, що в процесі розподілу ресурсів на х і х-у на k-му кроці отримали прибуток 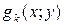і для подальшого розподілу засобів залишилось . Необхідно визначити управління, що максимізує повний прибуток від N -етапного процесу.

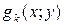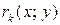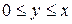Нехай, функції і неперервні при і , задовольняє подвійній нерівності

,

а 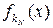– повний прибуток від 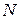-етапного процесу, який починається з величини на k-мукроці. Тоді для одноетапного процесу 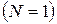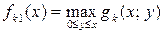. Аналогічно при 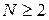отримаємо . Подвійні індекси значно ускладнюють обчислення, тому при записі функціональних рівнянь будемо використовувати один індекс. Вважатимемо, що кожному етапу відповідає певне значення 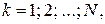і визначимо функцію 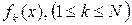як повний прибуток від процесу, що починається з величини на k-му етапі і закінчується на -му етапі, якщо витримується принцип оптимальності. Тоді одержимо наступні функціональні рівняння:

(5.8)

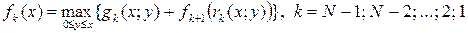(5.9)

Проілюструємо дію наведенного вище алгоритму на конкретному прикладі.

Приклад 5.1. Для розвитку двох галузей виробництва А і В на 3 роки виділено х засобів. Кількість засобів у, вкладених в галузь А, дозволяє отримати за один рік прибуток і зменшується до величини 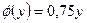. Кількість засобів х-у, вкладених в галузь В, дозволяє отримати за один рік прибуток 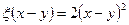і зменшується до величини .

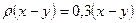Необхідно так розподілити виділені ресурси між галузями виробництва на роки планового періоду, щоб повний прибуток був максимальним.

Розв'язок. Період, тривалістю 3 роки, розіб'ємо на 3 етапи, співставивши кожному року один етап, тобто 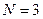, k =1; 2; 3. Розглядуваний процес є неперервним, хоча величини 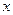і у на кожному етапі для наочності будемо відзначати індексами.

Знаходження оптимального розв'язку почнемо з третього етапу, на початку якого розподілу підлягає залишок засобів 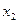з другого етапу. Для цього знайдемо оптимальне значення . Складемо вирази для функцій, що входять в рівняння (5.8) і (5.9):

;

.

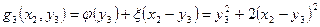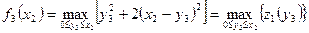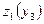Використовуючи класичні методи дослідження функції однієї змінної на екстремум, отримаємо, що в точці функція досягає мінімуму, який рівний .

Значення функції 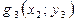на кінцях відрізка відповідно дорівнюють:

, .

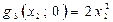Оскільки 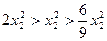, то функція 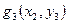досягає максимального значення на відрізку 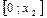при , і .

Таким чином, максимальний прибуток на останньому етапі досягається в тому випадку, якщо на початку етапу всі засоби, що залишилися з попереднього вкласти в розвиток галузі В.

Використовуючи рівняння (5.9), послідовно визначимо оптимальний розподіл засобів на другому і першому етапах.

Для другого етапу

, (5.10)

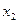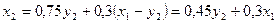де – сума засобів, що залишилася, якщо на 2 -ому етапі буде використано засобів в галузі А і – в галузі В, тобто . Тоді з (5.10) отримаємо для другого етапу:

.

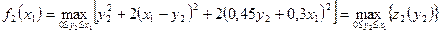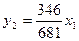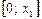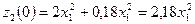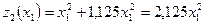Функція досягає мінімального значення при і воно приблизно дорівнює . На кінцях відрізка : , . Оскільки 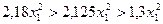, то функція 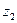приймає максимальне значення на відрізку при 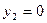. Тому .

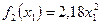Значить, максимальний прибуток на другому етапі буде досягнутий в тому випадку, коли на початок етапу всі засоби, що залишилися з попереднього, вкласти в розвиток галузі В.

Запишемо функціональне рівняння для першого етапу:

. (5.11)

Тут 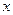, визначає кількість засобів, що залишилися від попереднього етапу. Враховуючи, що 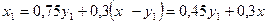отримаємо, що

.

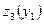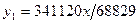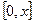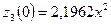Функція досягає мінімального значення при і воно приблизно дорівнює 1,35 . На кінцях відрізка : , . Оскільки 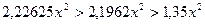, то функція 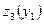приймає максимальне значення на відрізку 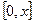при 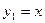і воно приблизно дорівнює 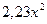. Таким чином, .

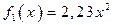Значить, максимальний прибуток на першому етапі отримаємо тоді, коли на його початку всі наявні засоби вкласти в розвиток галузі А.

Виходячи з проведеного розв'язування, робимо висновок, що на початок першого року всі виділені засоби необхідно вкласти в галузь А і їх кількість зменшується до величини . На початку другого року залишок засобів потрібно вкласти в галузь В і їх кількість зменшується до величини . На початок третього року залишок засобів 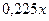знову вкладається в галузь В і зменшується до величини . При такому розподілі ресурсів максимальний дохід буде дорівнювати .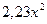

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
3. Автоматизація водорозподілу з комбінованим регулюванням
4. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
5. Автоматизація водорозподілу регулювання зі сталими перепадами
6. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
7. Автоматизація водорозподілу регулюванням за верхнім б'єфом
8. Автоматизація водорозподілу регулюванням за нижнім б'єфом
9. Альтернативні варіанти виробництва при повній зайнятості ресурсів
10. Альтернативність ресурсів і проблема економічного вибору
11. Амортизація як джерело фінансових ресурсів підприємств
12. Аналіз використання матеріальних ресурсів

Переглядів: 1879