• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Неперервна модель

У випадку, коли X – неперервна випадкова величина із щільністю розподілу ймовірностей 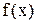, функція витрат має вигляд

. (3.15)

Щоб знайти мінімум функції 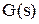, обчислимо її похідну, скориставшись формулою похідної від інтеграла по параметру. Одержуємо

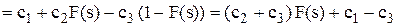
де – функція зрізаного розподілу попиту.

Прирівнюючи похідну до нуля, отримаємо рівняння, якому задовольняє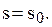

(3.16)

Для зручного обчислення функції G(s), вираз (3.15) можна представити у вигляді

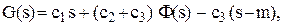(3.17)

де 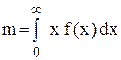– математичне сподівання розподілу попиту, а

, .

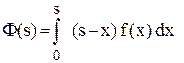Легко перевірити, що величина яка відповідає (3.16), дає мінімум економічної функції 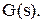Дійсно, знайдемо другу похідну від функції 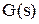і визначимо її знак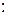

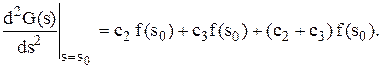
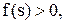Оскільки не дорівнює нулю і то 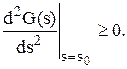Це означає, що функція 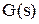має мінімум при

Співвідношення (3.16), яке визначає мінімум функції 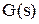у неперервному випадку, відповідає нерівностям (3.11), які відносяться до випадку, коли 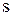набуває цілочислові значення.

Зокрема, для нормального розподілу попиту 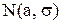з параметрами 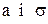із (3.16) маємо

де 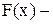функція нормального розподілу.

Таким чином, для визначення 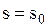одержуємо вираз

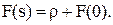
У Mathcad значення 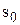визначається як квантиль нормального розподілу порядку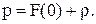

У випадку експоненціального розподілу попиту

.

Приклад 3.2.. Автотранспортна фірма здійснює обслуговування клієнтів, маючи 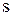власних автомобілів. Попит на транспортні послуги, виражений у кількості автомобілів, є дискретна випадкова величина X, задана рядом розподілу . Якщо у деякий день попит на автомобілі k нижче кількості наявних автомобілів s, то автомобілі, які безпосередньо не зайняті обслуговуванням клієнтів за замовленнями, використовуються на інших роботах, при цьому фірма втрачає прибуток у грош. од на один автомобіль. Якщо попит k вище кількості наявних автомобілів s, то для виконання своїх зобов’язань по обслуговуванню клієнтів у фірми виникає необхідність у оренді додаткових автомобілів, що веде до збитків у розмірі 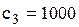грош. од на один автомобіль.

Треба визначити:

Ø оптимальну кількість автомобілів , яку повинна мати фірма щоденно, щоб можливі втрати прибутку були мінімальні;

Ø втрати від нестачі автомобілів (штрафи від незадовільненого попиту плюс втрата можливого прибутку);

Ø залежність загальних витрат від втрат у наслідок дефіциту;

Øзалежність математичного сподівання втрат від величини збитків 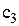у наслідок дефіциту автомобілів.

Читайте також:

1. G2G-модель електронного уряду
2. OSI - Базова Еталонна модель взаємодії відкритих систем
3. Абстрактна модель
4. Абстрактна модель
5. Абстрактна модель оптимального планування виробництва
6. Американська модель соціальної відповідальності
7. Англійський економіст У. Бріджез пропонує модель організаційних змін за такими напрямками.
8. Англо-американська модель
9. Англо-американська модель
10. Багатомірна лінійна модель регресії.
11. Багатосегментна модель
12. Багатоцільова багатокритеріальна модель обґрунтування рішень в полі кількох інформаційних ситуацій

Переглядів: 524