Поток событий

Університетська шкала оцінювання (100-бальна)	Національна шкала оцінювання (5-бальна)	Оцінка за шкалою ECTS (7-бальна)	Критерії визначення оцінки
90 – 100	(відмінно)	А	“відмінно” – студент глибоко і досконало знає матеріал усіх тем дисципліни, повністю засвоїв теоретичні основи курсу, ґрунтовно з’ясував закономірності історичного процесу
82 – 89	(добре)	В	“дуже добре” – студент у цілому добре засвоїв теоретичний матеріал дисципліни і здобув практичні навики на рівні, який дає можливість виконувати завдання з окремими неточностями (у визначенні дат, характеристиці особистостей, подій та явищ)
75 – 81	С	“добре” – студент добре засвоїв теоретичний матеріал дисципліни і здобув практичні навики на рівні, який дає можливість виконувати завдання на рівні вище середнього, втім, із декількома суттєвими помилками
68 – 74	3 (задовільно)	D	“задовільно” –студент непогано засвоїв теоретичний матеріал і набув практичних навичок, але це дозволяє йому посередньо виконувати завдання, оскільки кількість суттєвих помилок є значною
60 – 67	Е	“задовільно” – студент у загальних рисах орієнтується у теоретичному матеріалі і має практичні навички, достатні для виконання завдань на рівні мінімальних вимог
35 – 59	(незадовільно)	FХ	“незадовільно” – студентмає уявлення про теоретичний матеріал дисципліни, але при виконанні практичних завдань допускається дуже грубих помилок. Необхідно повторно опрацьовувати матеріал і складати предмет
1 – 34	F	“незадовільно” – студент не засвоїв матеріал навчальної дисципліни “Історія України”, не розуміє теоретичного матеріалу та не має практичних навичок для виконання поставлених завдань. Рекомендується обов’язкове повторне опрацювання курсу

Реферат

по дисциплине: «Теория вероятностей и математическая статистика»

на тему: Поток событий. Простейший поток и его свойства.

Выполнила:

студентка 6 курса

группы З-192/МО-ФМ

Специальность "Менеджмент"

Губеева О.Н.

Проверила:

ст.пр. Костина Е.Н.

Елабуга - 2014

Содержание

Поток событий…………………………………………………………3

Простейший поток…………………………………………………….5

Потоки Пальма и Эрланга…………………………………………….9

Поток событий

Потоком событий называется последовательность однородных событий, следующих одно за другим в случайные моменты времени.

Примерами могут быть:

- поток вызовов на телефонной станции;

- поток включений приборов в бытовой электросети;

- поток грузовых составов, поступающих на железнодорожную станцию;

- поток неисправностей (сбоев) вычислительной машины;

- поток выстрелов, направляемых на цель, и т. д.

При рассмотрении процессов, протекающих в системе с дискретными состояниями и непрерывным временем, часто целесообразно представлять процесс так, как будто изменения состояний системы происходят под действием каких-то потоков событий (поток вызовов, поток неисправностей, поток заявок на обслуживание, поток посетителей и т. д.) Поэтому имеет смысл рассмотреть подробнее потоки событий и их свойства,

Поток событий можно изобразить последовательностью точек на оси времени 0—7 (рис. 5.3, а), каждая из которых имеет определенную координату.

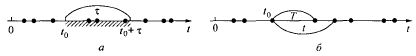
Рис. 5.3. Иллюстрация к определению потока событий (а), простейший поток (б)

Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. Такой поток сравнительно редко встречается на практике, но представляет определенный интерес как предельный случай. Чаще приходится встречаться с потоками событий, для которых и моменты наступления событий, и промежутки времени между ними случайны.

Рассмотрим потоки событий, обладающие некоторыми простыми свойствами [7].

1. Стационарность. Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок времени длиной т (рис. 5.3, а) зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок.

Стационарность потока означает его однородность по времени; вероятностные характеристики такого потока не меняются в зависимости от времени. В частности, так называемая интенсивность (или «плотность») потока событий — среднее число событий в единицу времени — для стационарного потока должна оставаться постоянной. Это, разумеется, не значит, что фактическое число событий, появляющихся в единицу времени, постоянно, поток может иметь местные сгущения и разрежения. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера, а среднее число событий, попадающих на единичный участок времени, остается постоянным для всего рассматриваемого периода.

На практике часто встречаются потоки событий, которые (по крайней мере, на ограниченном участке времени) могут рассматриваться как стационарные. Например, поток вызовов, поступающих на телефонную станцию, скажем, на интервале от 12 до 13 часов может считаться стационарным. Тот же поток в течение целых суток уже не будет стационарным (ночью интенсивность потока вызовов гораздо меньше, чем днем). Заметим, что так же обстоит дело и с большинством физических процессов, которые мы называем «стационарными» — в действительности они стационарны только на ограниченном участке времени, а распространение этого участка до бесконечности — лишь удобный прием, применяемый в целях упрощения.

2. Отсутствие последействия. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой (или другие, если рассматривается больше двух участков).

В таких потоках события, образующие поток, появляются в последовательные моменты времени независимо друг от друга. Например, поток пассажиров, входящих на станцию метро, можно считать потоком без последействия, потому что причины, обусловившие приход отдельного пассажира именно в данный момент, а не в другой, как правило, не связаны с аналогичными причинами для других пассажиров. Если такая зависимость появляется, условие отсутствия последействия оказывается нарушенным.

Рассмотрим, например, поток грузовых поездов, идущих по железнодорожной ветке. Если по условиям безопасности они не могут следовать один за другим чаще, чем через интервал времени 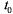, то между событиями в потоке имеется зависимость, и условие отсутствия последействия нарушается. Однако, если интервал 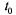мал по сравнению со средним интервалом между поездами, то такое нарушение несущественно.

3. Ординарность. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Ординарность означает, что события в потоке приходят поодиночке, а не парами, тройками и т. д. Например, поток клиентов, направляющихся в парикмахерскую, практически можно считать ординарным, чего нельзя сказать о потоке клиентов, направляющихся в ЗАГС для регистрации брака, и т. д.

Если в неординарном потоке события происходят только парами, только тройками и т. д., то можно его рассматривать как ординарный «поток пар», «поток троек» и т. д. Несколько сложнее обстоит дело, если число событий, образующих «пакет» (группу одновременно приходящих событий), случайно. Тогда приходится наряду с потоком пакетов рассматривать случайную величину X — число событий в пакете, и математическая модель потока становится более сложной.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Зміст семінарського заняття	\|	Классификация.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.035 сек.