• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Функція розподілу ймовірності.

Нехай існує сукупність дуже великої кількості N однакових молекул (наприклад, газ), що знаходиться в рівноважному стані. Припустимо, що деяка величина х, що характеризує молекулу (наприклад, обертальна чи коливальна енергія молекули), може приймати ряд дискретних значень:

, , …, , …

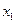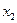Якби удалося виміряти одночасне значення величини 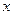у всіх 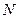молекул, то виявилося б, що у 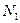молекул величина 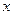має значення 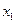, у молекул – 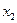, …, у 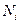молекул – значення і т.д.

Величина

(20.1)

називається імовірністю того, що величина 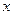має значення . Таке визначення імовірності придатне лише у випадку дуже великих N.

Зрозуміло, що 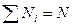. Тому

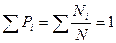. (20.2)

Таким чином, сума імовірностей усіх можливих значень величини х дорівнює одиниці.

Припустимо, що молекули характеризуються значеннями двох величин (наприклад, коливальної й обертальної енергій), кожна з який може приймати дискретні значення x_i i y_k. Відповідно до визначення (1.1) імовірності цих значень рівні

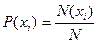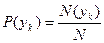, . (20.3)

Якщо значення однієї з величин не залежить від того, яке значення має інша, то величини x i y називаються статистично незалежними.

Знайдемо ймовірність 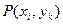того, що статистично незалежні величини мають одночасно значення i 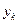. З (20.3) випливає, що значення x_i мають 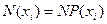молекул. Внаслідок статистичної незалежності у цих 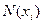молекул значення 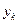будуть розподілені у тій самій пропорції, що і у всіх 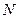молекул. Тому з числа 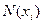значення 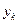будуть мати 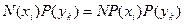молекул. Поділимо це число на 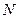, знайдемо ймовірність, яку шукаємо

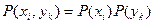. (20.4)

Ми прийшли до теореми про добуток ймовірностей, відповідно до якої імовірність одночасної появи статистично незалежних подій дорівнює добутку імовірностей цих подій. (У розглянутому вище випадку подією є те, що величина має дане значення.)

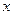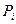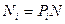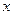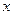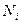Якщо ймовірність значення x_i величини рівна , то відповідно до формули (20.1) у молекул має значення . Сума значень величини у цих молекул буде рівна 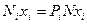, а сума значень 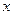у всіх 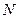молекул визначається виразом

.

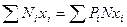Поділимо цю суму на 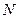, знайдемо середнє (за молекулами) значення величини х:

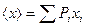. (20.5)

Отримана нами формула дозволяє, якщо ми знаємо ймовірності різних значень величини х, знайти середнє значення цієї величини.

Тепер розглянемо випадок, коли величина х, що характеризує молекулу, може приймати неперервний ряд значень від 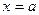до 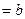(наприклад, 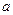i 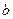можуть бути рівними 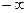і 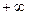). Прикладами таких величин можуть служити модуль поступальної швидкості чи кінетична енергія молекули. У цьому випадку число можливих значень х нескінченно велико, а кількість молекул хоча і дуже велика, але скінчена. Тому питання про те, яка кількість молекул має точно задане значення величини х, не має змісту - ця кількість дорівнює нулю.

У розглянутому випадку правомірним є питання про те, яка імовірність 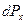того, що величина має значення, укладені в межах малого інтервалу 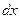, розташованого в околиці значення, рівного 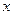(дане значення х повинне належати інтервалу 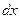). При малому 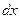ця ймовірність буде пропорційною 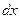. Крім того, вона залежить від того, у якому місці осі х розташований інтервал 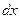, тобто є функцією 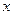. Таким чином,

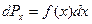(20.6)

(індекс 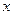при 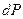указує значення 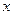, в околі якого знаходиться 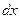). Функція 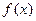називається функцією розподілу імовірності або густиною ймовірності.

Помноживши 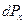на повну кількість молекул 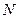, отримаємо кількість молекул 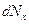, які мають значення 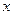, що розташовані у межах даного інтервалу :

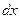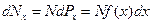. (20.7)

Інтеграл від 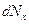, узятий по всьому інтервалу можливих значень 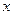(тобто "сума" 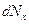), повинен дорівнювати повній кількості молекул :

.

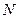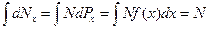Наслідком цього є співвідношення

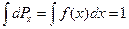. (20.8)

Формула (20.8) є аналогом формули (20.2). З умови (20.8) ми бачимо, що площа, обмежена графіком функції 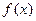, рівна одиниці.

Вираз 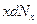дає суму значень 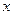, котрими володіють 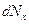молекул, а "сума" таких виразів, тобто

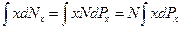(20.9)

дає суму значень 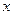усіх 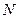молекул. Поділивши цю суму на 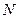, отримаємо середнє (за молекулами) значення величини :

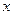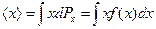. (20.10)

Ця формула є аналогом формули (20.5).

Якщо підставити в формулу (20.9) замість 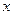деяку функцію цієї величини 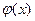, прийдемо до формули

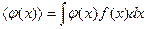. (20.11)

Згідно цієї формулі можна підрахувати, наприклад, середнє значення :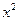

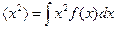. (20.12)

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
3. Автоматизація водорозподілу з комбінованим регулюванням
4. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
5. Автоматизація водорозподілу регулювання зі сталими перепадами
6. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
7. Автоматизація водорозподілу регулюванням за верхнім б'єфом
8. Автоматизація водорозподілу регулюванням за нижнім б'єфом
9. Аналіз ефективності використання каналів розподілу
10. Аналіз розподілу прибутку підприємства
11. Аналіз розподілу прибутку.
12. Аналіз розподілу чистого прибутку.

Переглядів: 800