
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Опір (резистор) у колі змінного струму
Генератор змінного струму замкнутий на зовнішнє коло з настільки малими індуктивністю та ємністю, що ними можна знехтувати. В колі є змінний струм
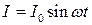 . (55.1)
. (55.1)
Знайдемо за яким законом змінюється напруга між кінцями кола а і б (рисунок 55.2). Застосувавши до ділянки кола аRб закон Ома, отримаємо
|
 . (55.2)
. (55.2)

Таким чином, напруга на кінцях ділянки також змінюється за законом синуса, причому різниця фаз між коливаннями струму та напруги дорівнює нулю. Напруга і струм одночасно досягають максимальних значень і одночасно обертаються в нуль (рисунок 55.3). Максимальне значення напруги
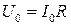 . (55.3)
. (55.3)
 Побудуємо векторну діаграму. Для цього оберемо вісь діаграми таким чином, щоб вектор, що зображає коливання струму, був напрямлений вздовж цієї вісі. Цю вісь називають віссю струмів. Вектор, що зображає коливання напруги, буде напрямлений вздовж вісі струмів, оскільки різниця фаз між струмом та напругою дорівнює нулю. Довжина цього вектора дорівнює амплітуді напруги
Побудуємо векторну діаграму. Для цього оберемо вісь діаграми таким чином, щоб вектор, що зображає коливання струму, був напрямлений вздовж цієї вісі. Цю вісь називають віссю струмів. Вектор, що зображає коливання напруги, буде напрямлений вздовж вісі струмів, оскільки різниця фаз між струмом та напругою дорівнює нулю. Довжина цього вектора дорівнює амплітуді напруги 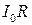 .
.
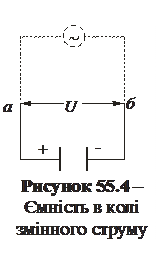 Ємність (конденсатор) у колі змінного струму.
Ємність (конденсатор) у колі змінного струму.
Позначимо різницю потенціалів точок а і б (рисунок 50.4) через  (
(  ). Тоді
). Тоді 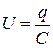 . Але
. Але  , тоді
, тоді  . Якщо сила струму в колі змінюється за законом
. Якщо сила струму в колі змінюється за законом 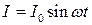 , то
, то  . Стала інтегрування С' позначає довільний сталийзаряд конденсатора, не пов'язаний з коливаннями струму, а тому покладемо
. Стала інтегрування С' позначає довільний сталийзаряд конденсатора, не пов'язаний з коливаннями струму, а тому покладемо 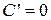 . Отже
. Отже
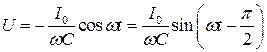 . (55.4)
. (55.4)
При синусоїдальних коливаннях струму в колі напруга на конденсаторі змінюється також за законом синуса, однак між коливаннями струму та напруги існує різниця фаз. Коливання напруги на конденсаторі відстають від коливання струму за фазою на 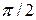 .
.
Амплітуда напруги на конденсаторі дорівнює
 . (55.5)
. (55.5)
Величина
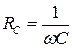 (55.6)
(55.6)
відіграє роль опору ділянки кола. Вона називається ємнісним опором.
 Вектор, що відображає коливання напруги на векторній діаграмі в цьому випадку не співпадає з віссю струму. Він розвернутий у від'ємному напрямку (за годинниковою стрілкою) на кут
Вектор, що відображає коливання напруги на векторній діаграмі в цьому випадку не співпадає з віссю струму. Він розвернутий у від'ємному напрямку (за годинниковою стрілкою) на кут 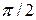 .
.
Читайте також:
- Автоматичне розвантаження по струму.
- Активний опір у ланцюзі синусоїдального струму
- Баланс потужностей у колі гармонічного струму.
- Безпечні методи звільнення потерпілого від дії електричного струму.
- Будова машин постійного струму
- В електронагрівачах використано одну з головних властивостей електричного струму - здатність нагрівати провідники.
- Величина густини зварювального струму
- Вибір значення розрахункового струму.
- Види двигунів постійного струму.
- Види електричних травм та дії електричного струму на людину.
- Вимiрювання постiйних струму та напруги
- Вимірювальні трансформатори струму і напруги
| <== попередня сторінка | | | наступна сторінка ==> |
| Теоретичні відомості | | | Індуктивніть (котушка) в колі змінного струму. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |