
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Моделі дуополії і теорія ігор
Суть моделі Курно полягає в тому, що рівновага на ринку, який представлений двома фірмами , що виробляють однорідну продукцію, досягається за відомого ринкового попиту, коли виробництво однієї з фірм регулюється при умові фіксованого обсягу виробництва іншої продукції.
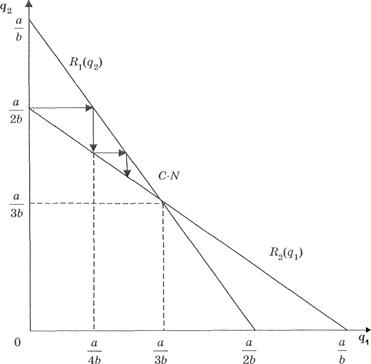
Рис.2 Рівновага дуополії Курно за сталих витрат
Функція реакції для цієї моделі відображає залежність обсягу випуску даної фірми від обсягу випуску іншої фірми на ринку.
Вирішивши систему рівнянь, отримуємо рівноважні рішення моделі. Рівновага на ринку забезпечується випусками
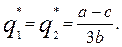
Графічна ілюстрація представлена на рис.3.
Загальний обсяг пропозиції на ринку буде становити:
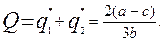
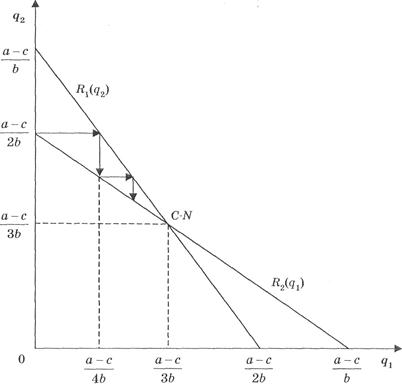
Рис.3. Рівновага дуополії Курно за сталих витрат
Ринкова ціна дорівнюватиме:
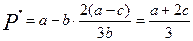 ,
,
що дає змогу кожному дуополісту отримати прибуток в обсязі
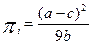
Модель Стакельберга Виходить із припущення про різну економічну силу конкурентів. Лідер як сильніший і такий що має певну монопольну владу визначає для себе ціну та обсяги реалізації продукції, які максимізують прибуток. Інші фірми – аутсайдери, визначають для себе обсяг, який максимізує прибуток.
Модель Бертрана Основне припущення цієї модулі базується на виборі фірмових не обсягів виробництва, а ціни, при цьому економічна сила конкурентів однакова.
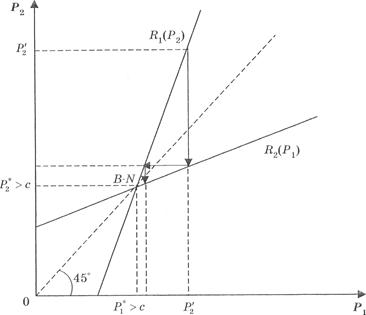
Рис. 4. Рівновага дуополії Бертрана при випуску неоднорідної продукції
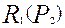 та
та 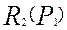 — криві реагування олігополістів. Графічно рівновага Бертрана — Неша визначається перетином кривих реакції дуополістів (точка В-N) у просторі цін. Рівновага досягається, якщо припущення дуополістів щодо цінової поведінки виправдовуються. Якщо дуополіст 1 вважає, що його суперник призначить ціну
— криві реагування олігополістів. Графічно рівновага Бертрана — Неша визначається перетином кривих реакції дуополістів (точка В-N) у просторі цін. Рівновага досягається, якщо припущення дуополістів щодо цінової поведінки виправдовуються. Якщо дуополіст 1 вважає, що його суперник призначить ціну 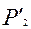 , то з метою максимізації прибутку він обере ціну згідно із кривою реагування
, то з метою максимізації прибутку він обере ціну згідно із кривою реагування 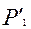 . У відповідь на це дуополіст 2 також змінить ціну. Таким чином вони прийдуть до рівноважних цін
. У відповідь на це дуополіст 2 також змінить ціну. Таким чином вони прийдуть до рівноважних цін 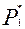 та
та 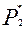 , які для моделі диференційованої продукції будуть вищі, ніж граничні витрати.
, які для моделі диференційованої продукції будуть вищі, ніж граничні витрати.
За ціною 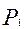 >
> 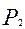 попит на продукцію буде дорівнювати нулю, оскільки всі покупці купуватимуть у конкурента. За умов однакової ціни фірм ринок буде поділений навпіл, що відповідає точці Р. Коли ціна фірми 1 буде меншою за ціну фірми 2, то весь ринковий попит буде забезпечувати фірма 1. При цьому доцільно розглядати ділянку ВМ кривої попиту, оскільки беззбитковість передбачає, що ціна повинна бути не меншою за середні витрати.
попит на продукцію буде дорівнювати нулю, оскільки всі покупці купуватимуть у конкурента. За умов однакової ціни фірм ринок буде поділений навпіл, що відповідає точці Р. Коли ціна фірми 1 буде меншою за ціну фірми 2, то весь ринковий попит буде забезпечувати фірма 1. При цьому доцільно розглядати ділянку ВМ кривої попиту, оскільки беззбитковість передбачає, що ціна повинна бути не меншою за середні витрати.
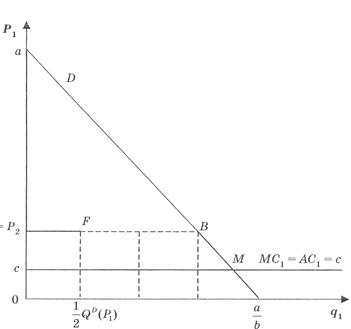
Рис. 5. Крива попиту дуополіста Бертрана
Ситуація рівноваги в моделі дуополії Бертрана за умови однорідності продукції, коли в умовах рівноваги ціна буде дорівнювати граничним витратам, має назву парадокса Бертрана.
Стратегічну поведінку в дуополії найадекватніше відображають моделі теорії ігор. Це теорія індивідуальних раціональних рішень, які приймаються учасниками гри в умовах недостатньої інформації щодо результатів цих рішень. Основними поняттями теорії ігор є такі:
Гравець — це особа, що приймає рішення (наприклад, фірма), учасник гри.
Функція платежів — цільова функція гравця, яка встановлює зв'язок між варіантом дій та значенням функції — виграшем гравця, що вимірюється певною корисністю для нього (наприклад, прибутком для фірми).
Гра — це сукупність відомих усім гравцям правил, які визначають можливі дії гравців та наслідки й виграші від кожної окремої дії.
Хід — момент гри, коли гравці повинні зробити вибір одного з можливих варіантів дій.
Партія гри — певна визначена сукупність ходів і виборів.
Стратегія — це набір правил, які формулюються до гри і визначають вибір варіанту дій гравця в залежності від можливих дій суперників.
Ігри з двома учасниками мають назву ігор двох осіб. Якщо виграш одного учасника дорівнює програшу іншого, то це зветься грою із нульовою сумою. Гра з ненульовою сумою має місце, коли кожен з учасників може виграти від рішення одного з них. Гра зветься кооперативною, якщо припускається змова гравців, і некооперативною, якщо змова неприпустима.
Результати дій учасників у грі двох осіб відбиваються у матриці виграшів, яка показує виграш кожного з учасників при будь-якій з можливих пар їхніх стратегій.
Для поглиблення аналізу стратегічних рішень, які приймаються фірмами, в мікроекономіці широко використовується теорія ігор. У будь-якій грі найважливіший аспект розробки стратегії — це розуміння точки зору супротивника (за умови, що опонент — раціональна особа), виведення висновку щодо можливості реакції його (чи її) на ваші дії.
Завдання, що стоїть перед олігополістичними фірмами, характеризує класичний приклад із теорії ігор, названий «дилемою ув'язнених».
Суть його полягає ось у чому: двох заарештованих осіб звинувачують у скоєнні злочину. Вони знаходяться в окремих камерах в'язниці, а тому не можуть спілкуватися між собою. Від кожного з них вимагають признатися. Якщо свою вину визнають обидва арештанти, кожен із них одержить строк ув'язнення п'ять років, якщо жоден із них не признається, то обвинувачувальний вирок важко буде винести. Тому ув'язнені можуть розраховувати на поблажливість і одержати строк ув'язнення два роки.
З іншого-боку, якщо один із ув'язнених визнає свою вину, а другий — ні, то особу, яка визнала себе винною, буде засуджено на рік ув'язнення, а інший перебуватиме у в'язниці десять років. Що б ви зробили на місці цих ув'язнених — призналися чи ні?
Матриця виграшів (табл. 1) систематизує всі можливі наслідки (зауважте, що «виграш» має негативне значення). Наприклад, запис у нижньому правому кутку матриці означає дворічний строк ув'язнення для кожного із заарештованих).
Як видно з таблиці, ув'язнені постають перед дилемою. Якби вони могли домовитися не зізнаватися, то кожен із них відбував би у в'язниці лише два роки.
Таблиця 1.
Матриця виграшів для «дилеми ув’язнених»
| Ув'язнений А | Ув'язнeний Б | |
| Зізнався | Не зізнався | |
| Зізнався | -5,-5 | -1,-10 |
| Не зізнався | -10,-1 | -2,-2 |
Проте вони не можуть спілкуватися, а навіть якби могли, чи можуть вони довіряти один одному? Якщо ув'язнений А не визнає себе винним, він ризикує бути зрадженим своїм колишнім спільником. Урешті-решт, що не робив би ув'язнений А, ув'язнений Б своїм признанням здобуває для себе перевагу. Так само своїм признанням ув'язнений А виявляє ініціативу, отже, ув'язнений Б має замислитися над тим, чи не виграє А за його рахунок.
Отже, обидва ув'язнені, очевидно, признаються і одержать по п'ять років ув'язнення.
Особливості поведінки олігополіста на ринку визначаються двома тенденціями:
1. Фірми зацікавлені в максимізації сукупного прибутку галузі завдяки спільним діям, оскільки це дає змогу реалізувати монопольну владу.
2. Кожна фірма прагне отримати надприбуток за рахунок конкуренції, порушуючи угоду.
Суперечності двох тенденцій ілюструє дилема олігополіста.
Кожна фірма (А і Б) за існуючих цін отримує певний прибуток. Вона може його збільшити, якщо зменшить ціну, але за умови, що конкурент залишає свою ціну без змін. Тобто кожна фірма має дві стратегії:
· Зменшити ціну;
· Залишити ціну без змін.
Таблиця 2.
Матриця виграшів для фірм –дуополістів
| Стратегії фірми А | |||
| Стратегії фірми Б | Зменшити ціну | Зменшити ціну | Залишити ціну без змін |
| Прибуток А: 60 тис. Прибуток Б: 100 тис. | Прибуток А: 30 тис. Прибуток Б: 100 тис. | ||
| Залишити ціну без змін | Прибуток А: 100 тис. Прибуток Б: 30 тис. | Прибуток А: 75 тис. Прибуток Б: 75 тис. |
Для кожної пари стратегій відомі виграші обох гравців — їхні прибутки (збитки), тобто можна побудувати матрицю виграшів.
Для розв'язання дилеми фірми-гравці можуть скористатися максимінною стратегією: спочатку кожна фірма для кожної зі своїх стратегій підраховує по два результати, які можна забезпечити залежно від стратегії, обраної конкурентом. Серед цих результатів фірма знаходить варіант із мінімальним виграшем (песимістична оцінка кожної власної стратегії). Після цього фірма робить вибір на користь тієї стратегії, яка має максимальну оцінку з усіх песимістичних. Так, фірма А при виборі стратегії 1 може отримати прибуток 60 або прибуток 100 (залежно від дій Б): мінімальна оцінка — 60. При виборі стратегії 2 — відповідно min (30; 75) 30; тоді максимальна оцінка із двох (60 і 30), тобто 60, досягається, якщо обрати стратегію зниження цін. 60 тис. — це безумовний прибуток, який може бути навіть більшим (тобто 100).
Аналогічно для фірми Б мінімальні оцінки стратегій будуть: для 1-ї — тіп (60; 100) 60; для 2-ї - min (30; 75) 30, тоді максимінною стратегією для фірми буде перша — зменшити ціну з виграшем max (60; 30) 60.
У наведеному прикладі обидві фірми мають домінантну стратегію — таку, яка забезпечує найкращий результат порівняно з іншими стратегіями, незалежно від дій конкурента.
Оскільки цінова конкуренція для учасників олігополії надто небажана, центр ваги конкурентної боротьби переноситься в нецінову сферу. Це може бути боротьба за глибшу диференціацію продукту, підвищення його якості, використання ефективної реклами і т. ін. Це служить стабілізуючим фактором для олігопольних галузей, тобто нецінова конкуренція дає змогу отримати більш довгострокові переваги над конкурентами, порівнюючи з ціновими маневрами, які легко тиражуються.
Читайте також:
- CMM. Визначення моделі зрілості.
- E) теорія раціонального вибору.
- I. Теорія граничної продуктивності і попит на ресурси
- ISO 15504.Структура еталонної моделі
- V теорія граничної корисності визначає вартість товарів ступенем корисності останньої одиниці товару для споживача.
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 10. Недоскональна конкуренція: олігополія та монополістична конкуренція | | | Монополістична конкуренція. Сутність і характерні риси |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |