• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тема 6. Нелінійні оптимізаційні моделі економічних систем

Якщо цільова функція або обмеження задачі математичного програмування містить змінні в степені 2 чи більше, то маємо справу із задачею нелінійного програмування.

Задачі нелінійного програмування можна розв’язати за допомогою пошуку рішення в Excel, однак необхідно враховувати що вони можуть містити більше одного розв’язку, тоді як пошук рішення показує лише один з них.

Для вирішення задач нелінійного програмування з обмеженнями у вигляді рівнянь можна застосовувати метод множників Лагранжа.

Приклад 6.1

Для виготовлення квасу, попит на який становить 250 пляшок на день, можна використовувати дві виробничі лінії. Витрати при використанні першої лінії становлять 5x₁+2x₁² грн., другої – 7x₂+x₂² грн. Визначити, скільки пляшок квасу виготовляти на кожній виробничій ліній, щоб сукупні витрати були мінімальними.

Розв’язання

Економіко-математичну модель задачі можна представити у наступному вигляді:

Складемо функцію Лагранжа, де λ – невизначений множник Лагранжа:

.

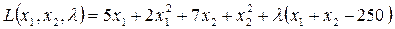Знайдемо частинні похідні функції Лагранжа за змінними х₁, х₂ і λ та прирівняємо їх до 0:

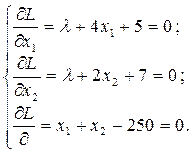
Цю систему можна розв’язати методом Крамера або Жордана-Гаусса.

Отримуємо розв’язки: x₁≈84; х₂≈166; λ≈-340.

Отже, на першій лінії доцільно виробляти 84 пляшки квасу, а на другій – 166.

Розв’яжемо цю ж задачу за допомогою Excel.

F6 містить формулу =СУММПРОИЗВ(B3:E3;B6:E6). Викликаємо пошук рішення.

Натискаємо «Выполнить».

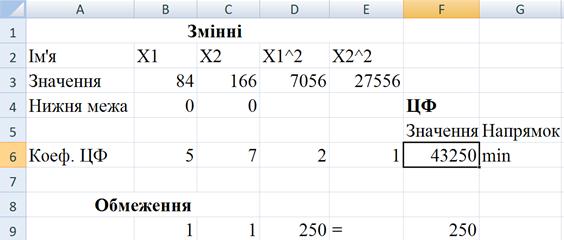
Як бачимо, рішення задачі, знайдені за допомогою різних методів, збігаються.

Питання для самостійного вивчення: теорема Куна-Таккера, сідлові точки.

Читайте також:

1. Active-HDL як сучасна система автоматизованого проектування ВІС.
2. CMM. Визначення моделі зрілості.
3. D – моделювання в графічній системі КОМПАС
4. D. СОЦИОИДЕОЛОГИЧЕСКАЯ СИСТЕМА ВЕЩЕЙ И ПОТРЕБЛЕНИЯ
5. H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
6. I. Органи і системи, що забезпечують функцію виділення
7. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
8. II. Анатомічний склад лімфатичної системи
9. II. Бреттон-Вудська система (створена в 1944 р.)
10. II. Найважливіші проблеми, що визначають розвиток місцевого самоврядування і є спільними для будь-яких урядових систем.
11. III етап. Системний підхід
12. III. центральная нервная система

Переглядів: 592