• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівняння нерозривності деформацій

Співвідношення Коші (1.36) зв'язують між собою шість складової деформації й три складові переміщення, але цей зв'язок не є взаємно однозначним. Якщо задані три складові переміщення, то шість складових деформації визначаються однозначно. Якщо ж задані шість складової деформації, то для визначення трьох складові переміщення потрібно проінтегрувати шість диференціальних рівнянь у частинних похідних. При довільному виборі складових деформації шість рівнянь із трьома невідомими не завжди можуть бути розв’язані однозначно, тому між шістьма складовими деформації повинні існувати певні залежності.

Виключимо складові переміщення з рівнянь (1.36).

Двічі продиференціюємо перше рівняння по 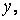а друге — по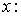

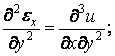
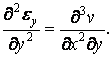
Складемо два останніх вирази:

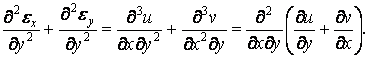
(1.41)

В дужках (1.41) записані кутова деформація 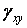й тоді

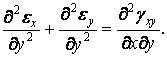
(1.42)

Аналогічно для двох інших координатних площин

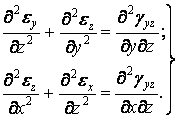
(1.43)

Рівняння (1.42), (1.43) означають, що якщо задані дві лінійні деформації у взаємно перпендикулярних напрямках, то кутову деформацію в площині цих лінійних деформацій не можна задати довільно. Для забезпечення однозначності розв’язку цих рівнянь недостатньо, тому що вони отримані диференціюванням, а при цьому порядок диференціального рівняння підвищується й можлива поява нових розв’язків, які не задовольняють вихідному рівнянню.

Продиференціюємо три останніх рівняння (1.36):

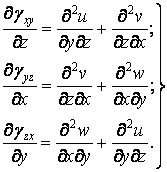
(1.44)

Складемо перші два рівняння й віднімемо третє:

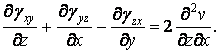
Продиференціюємо цей вираз по 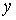і, враховуючи, що

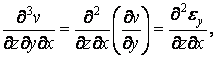
одержимо

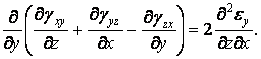
(1.45)

Ще два рівняння записуються аналогічно:

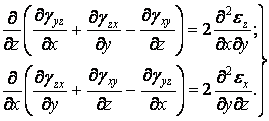
(1.46)

Таким чином, отримана система шести диференціальних рівнянь у частинних похідних:

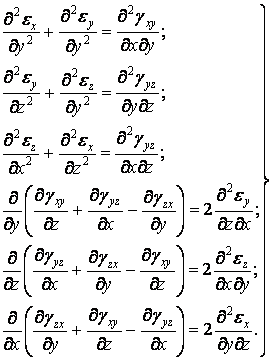
(1.47)

Рівняння (1.47) називаються рівняннями нерозривності деформацій Сен-Венана.

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. R – розрахунковий опір грунту основи, це такий тиск, при якому глибина зон пластичних деформацій (t) рівна 1/4b.
3. V Процес інтеріоризації забезпечують механізми ідентифікації, відчуження та порівняння.
4. VІI. Утворіть вищий та найвищий ступені порівняння від прислівників із вправи VI.
5. Асимптотичний підхід до порівняння оцінок
6. Бюджетний контроль - це порівняння показників бюджету зі звітом за від­повідний період часу.
7. В обох випадках основним розрахунковим рівнянням є рівняння теплопередачі і теплового балансу
8. Векторне канонічне параметричне рівняння прямої в просторі.
9. Взаємозв'язок між тензорами напруг і деформацій. Узагальнений закон Гука
10. Вивід основного рівняння фільтрації
11. Види деформацій
12. Види навантажень і основних деформацій

Переглядів: 634