• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Коло з паралельним з’єднанням нелінійних опорів

Розглянемо нелінійне коло, схема якого зображена на рис. 2.9.

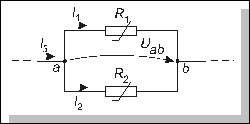
Рис. 2.9

Нехай задані ВАХ резисторів R₁та R₂ (рис. 2.10,а та рис. 2.10,б).

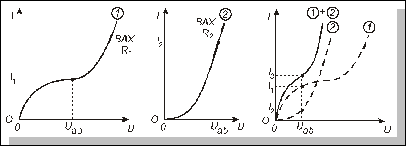
Рис. 2.10

Якщо задана також величина U_ав, а треба знайти величини I₁ та I₂, то розв’язання просте і базується на тому факті, що U_ав прикладене до кожного з резисторів. Тому, відклавши величину U_ав на кожній окремій ВАХ, знайдемо шукані струми I₁ та I₂ (рис. 2.10,а та рис. 2.10,б).

Якщо ж U_ав не задана, а заданий струм I₃ в нерозгалуженій частині кола, то розв’язання потребує додаткових графічних побудувань. Спочатку звернемо увагу на те, що за будь-якої напруги U_ав величина I₃ (яка, звісно, залежить від U_ав) визначається за першим законом Кірхгофа як

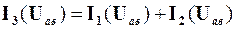. (2.4)

Але 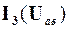є ВАХ ділянки ав. Таким чином, з виразу (2.4) випливає, що ВАХ резистора, еквівалентного ділянці ав, утворюється шляхом додавання величини струмів окремих резисторів при кожному значенні напруги U_ав, тобто додаванням графіків окремих ВАХ за струмом (рис.2.10,в).

Маючи сумарну ВАХ, знаходимо напругу U_ав, при якій струм у нерозгалуженій частині кола дорівнює заданому I₃. Для цього відкладаємо величину I₃ на осі струмів і проводимо крізь цю точку горизонталь до перетину із сумарною ВАХ (крива 1+2 на рис.2.10,в). Напруга, яка відповідає точці перетину, і буде шуканою напругою U_ав. Струм I₁знаходимо як струм, який відповідає цій напрузі на ВАХ резистора R₁, аналогічно знаходимо струм I₂ за ВАХ резистора R₂ (або як I₂ =I₃–I₁).

Корисне узагальнення.При довільній кількості резисторів, з’єднаних паралельно, сумарна ВАХ теж будується шляхом додавання за струмом ВАХ окремих резисторів, які входять у це з’єднання.

Читайте також:

1. Аналіз трифазного з’єднання з урахуванням опорів лінійних проводів
2. Визначення коефіцієнтів чотириполюсника за матрицею власних та взаємних опорів методу контурних струмів.
3. Вимірювання опорів
4. Вимірювання опорів за допомогою магнітоелектрич­ного вимірювального механізму
5. Вимірювання опорів методом заміщення
6. ВИРІШЕННЯ НЕЛІНІЙНИХ ЗАДАЧ УМОВНОЇ ОПТИМІЗЦІЇ МЕТОДОМ ЛАНГРАНЖА
7. Додаткова інформація щодо методів розрахунку нелінійних резистивних кіл
8. Еквівалентні перетворення схем з'єднань опорів
9. Елементи опорів та реостати
10. Еліпс, гіпербола, парабола з осями, паралельними осям координат
11. Закономірності, загальні для лінійних та нелінійних кіл постійного струму
12. Коефіцієнти місцевих опорів

Переглядів: 527