• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Основні відомості про комплексні числа

Комплексне число – це число виду А=а+jв, де а та в – дійсні числа, а j=Ö-1 – так звана уявна одиниця. Величину а називають дійсною частиною комплексного числа (умовне позначення а =Re{A}), величину в називають уявною частиною комплексного числа (умовне позначення в= Im{A}). В радіоелектроніці комплексне число позначають літерою з підкреслюванням.

Вираз А являє собою алгебраїчну форму записукомплексного числа. Розглянемо площину з декартовими прямокутними координатами, в яких вісь абсцис є віссю дійсних чисел, а вісь ординат – віссю уявних чисел. З алгебраїчної форми запису випливає графічне зображення комплексного числа А у вигляді точки з координатами (а, в) (рис.4.2).

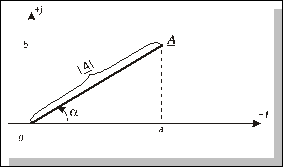
Рис. 4.2

Розглянемо нижній з двох прямокутних трикутників, наявних на рис.4.2. Довжина катета, який розташовано на осі дійсних чисел, дорівнює а, а довжина катета, який розташовано на осі уявних чисел, дорівнює в, тому гіпотенуза ОА дорівнює 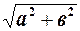. Позначимо її як 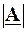. Ця гіпотенуза утворює кут a з віссю дійсних чисел, тому з того ж прямокутного трикутника випливає, що a= 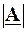cosa , в= 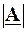sina, а отже

.

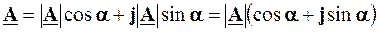Останній вираз називають тригонометричною формою записукомплексного числа, величину 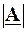називають модулемабо абсолютною величиноюкомплексного числа 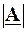, а величину a – аргументом комплексного числа А.

Використання формули Ейлера

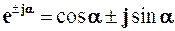
дозволяє перейти від тригонометричної форми запису комплексного числа до його показникової (експоненціальної) формизапису

.

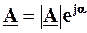Звідси випливає ще один спосіб графічного зображення комплексного числа – його зображення у вигляді вектора довжиною 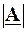, спрямованого під кутом a до позитивного напрямку осі дійсних чисел.

Для переходу від алгебраїчної форми запису до показникової форми запису використовують такі співвідношення:

;

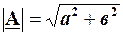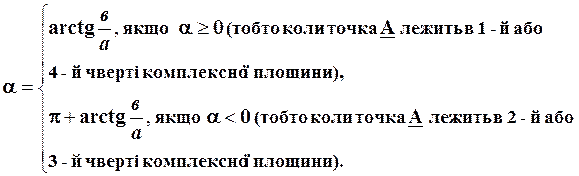
Отже, 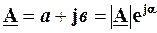Число 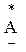називають комплексно-спряженимчислу А, якщо .

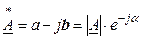Додавання та віднімання комплексних чисел виконують, попередньо привівши їх до алгебраїчної форми запису:

;

;

.

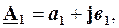
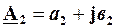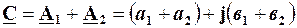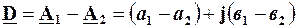Ці операції можна також виконати графічно (з точністю, обмеженою точністю графічних побудувань), користуючись правилами додавання та віднімання векторів (рис. 4.3).

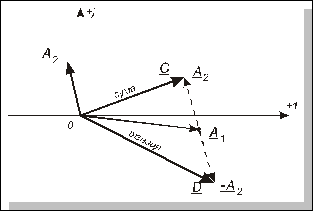
Рис. 4.3

Множення комплексних чисел виконують як в алгебраїчній, так і в показниковій формі запису:

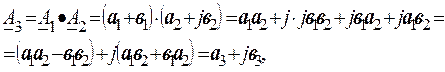
де j×j= - 1;

.

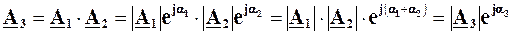Ділення комплексних чисел теж можна виконувати як в алгебраїчній, так і в показниковій формі запису.

.

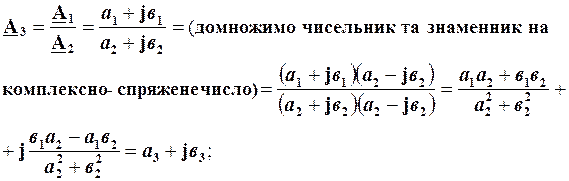
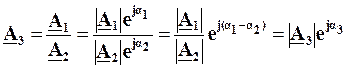Звичайно множення та ділення зручніше виконувати в показниковій формі запису.

Зауважимо, що згідно з формулами Ейлера, маємо:

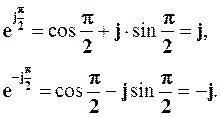
Тоді

.

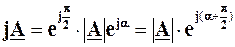
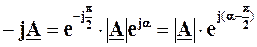Звідси випливає, що множення числа А на j (або, що те ж саме, на 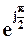) призводить до того, що вектор добутку утворюється з вектора А шляхом повороту останнього на 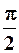проти годинникової стрілки без зміни довжини вектора. Множення ж на (-j) числа А (або, що те ж саме, його множення на 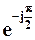) утворює вектор добутку шляхом повороту вектора А на 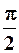за годинниковою стрілкою. Ці результати ілюстровані рис. 4.4.

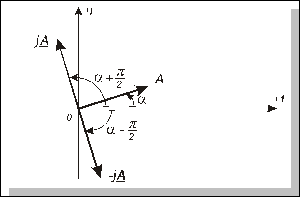
Рис. 4.4

Взагалі, множення комплексного числа на 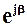призводить до повороту вектора, який зображує це число, на кут b проти годинникової стрілки, якщо b>0, або за годинниковою стрілкою, якщо, b<0.

Отже, якщо кут повороту b є пропорційним часу, тобто b = wt, то множення комплексного числа А на 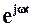призведе до утворення нового вектора 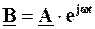, який являє собою той же вектор А, який безупинно обертається проти годинникової стрілки з кутовою частотою w, – так званий обертовий вектор.

Читайте також:

1. II. Множення круглих багатоцифрових чисел на розрядні числа.
2. II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
3. II. Основні засоби
4. II.3. Основні способи і прийоми досягнення адекватності
5. IX. Відомості про військовий облік
6. IX. Відомості про військовий облік
7. Q Конституція України від 28 червня 1996 р. // Відомості Верховної Ради України – 1996 - № 30 – Ст. 141
8. V Практично всі психічні процеси роблять свій внесок в специфіку організації свідомості та самосвідомості.
9. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
10. Абсолютна величина дійсного числа
11. Абсолютна величина числа позначається символом .
12. Адвокатура в Україні: основні завдання і функції

Переглядів: 840