• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Комплекси струмів, напруг та ЕРС. Векторна діаграма. Суть символічного методу розрахунку

Розглянемо деякий обертовий вектор 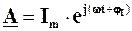. Записавши комплексну експоненту за формулою Ейлера, отримаємо

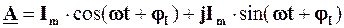. (4.3)

Якщо I_m має фізичний сенс амплітуди деякого струму, w – його кутової частоти, а j_I – його початкової фази, то можна зробити висновок, що миттєве значення синусоїдного струму 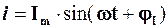є проекцією введеного вище обертового вектора А на вісь уявних чисел, тобто 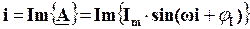. Звідси випливає, що будь-якому синусоїдному струмові можна зіставити індивідуальний обертовий вектор, який однозначно зв’язаний з цим струмом. Звичайно цей обертовий вектор позначають , поставивши крапку над позначенням миттєвої величини струму:

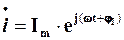(4.4)

Величину 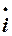називають комплексом миттєвого значенняструму. Він є символічним зображенням реального синусоїдного струму, а відповідний обертовий вектор на комплексній площині є символічним графічним зображенням цього ж струму.

Вираз (4.4) може бути записаний у дещо іншому вигляді

,

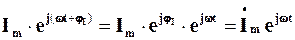де 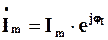– так звана комплексна амплітуда струму.

У розрахунках також використовують комплекс дійсного значеннясинусоїдного струму

,

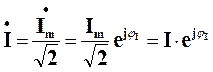де I – діюче значення струму (див. п. 4.1 3).

Аналогічно тому, як це було зроблено для струмів, вводять обертові вектори напруги та ЕРС, а також комплекси їх миттєвих значень 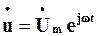та , де 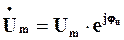– комплексна амплітуда напруги,

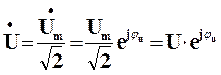– комплекс діючого значення напруги,

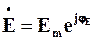– комплексна амплітуда ЕРС,

– комплекс діючого значення ЕРС.

Якщо є кілька векторів (наприклад, 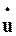, 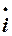та 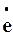), які обертаються з однаковою кутовою частотою w, то один відносно одного вони нерухомі. Тому в цьому випадку наявність обертання достатньо тільки мати на думці, а на комплексній площині слід зображувати розташування цих векторів при t=0.

Таке зображення синусоїдних струмів, напруг та ЕРС, як векторів на комплексній площині, називають векторною діаграмою відповідно струмів, напруг або ЕРС.

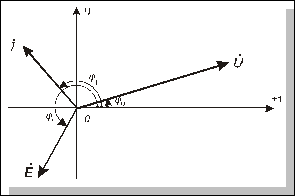
Рис. 4.5

Наприклад, на рис. 4.5 зображено векторну діаграму комплексів діючих значень (векторна діаграма може бути побудована і для комплексних амплітуд; різниця буде тільки в довжині векторів – вони будуть у Ö2 разів довші). Нагадаємо, що напрямок позитивного відліку кута – проти годинникової стрілки.

У читача може виникнути питання: навіщо замінювати, наприклад, опис напруги у вигляді синусоїдної функції часу, яку можна наочно побачити на екрані осцилографа (приладу, який зображує розвиток електричних процесів у часі), на якийсь абстрактний вектор на комплексній площині або на комплексну амплітуду?

Відповідь полягатиме в такому. Якщо описувати струми, напруги та ЕРС кола виключно у вигляді їх миттєвих значень (наприклад, 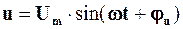), то й систему рівнянь за законами Кірхгофа, потрібну для обчислення шуканих струмів (або інших величин) складати треба теж для миттєвих значень. Але тоді в процесі розв’язання цієї системи рівнянь виникне потреба в громіздких тригонометричних перетвореннях. Перехід до комплексних амплітуд або комплексів діючих значень струмів, напруг та ЕРС дозволяє, як це побачить читач на наступних сторінках цього підручника, при розрахунку кола методом рівнянь Кірхгофа (або будь-яким іншим методом) складати необхідні рівняння та виконувати обчислення точнісінько так само, як це робилося для кіл постійного струму, тобто на базі звичайних алгебраїчних прийомів. “Платою” за цю зручність є необхідність використовувати для позначення коливань та опорів дещо нову символіку (наприклад, 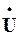замість U, 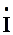замість I, Z замість R і т. д). Заміна миттєвих значень електричних коливань, а також опорів, на їх символічні зображення з подальшим складанням та розв’язанням звичайних алгебраїчних (а не тригонометричних) рівнянь кола складає суть символічного(іноді його звуть комплексним) методу розрахунку електричних кіл синусоїдного струму.

Існують певні обмеження застосування символічного методу, а саме: його можна застосовувати для розрахунку тільки тих кіл, в яких не відбувається нелінійних перетворень миттєвих значень електричних коливань. Прикладами нелінійних перетворень є логарифмування коливання, множення двох коливань і т. ін. Але доки ми розглядатимемо лінійні електричні кола на ці обмеження можна не звертати уваги.

Дещо детальніше про математичні основи символічного методу розрахунку кіл та про властиві йому обмеження можна дізнатися з класичної праці [10].

Читайте також:

1. D) методу мозкового штурму.
2. V Ідентифікація, раціоналізація, проекція, інтроекція, агресія, зворотна реакція та їх комплекси.
3. Алгоритм маркетингового розрахунку цін.
4. Алгоритм розрахунку апаратів псевдозрідженого шару.
5. Алгоритм розрахунку майбутньої вартості ануїтету
6. Алгоритм розрахунку майбутньої вартості грошей за простими і складними відсотками
7. Алгоритм розрахунку основних фінансових показників (коефіцієнтів)
8. Алгоритм розрахунку ризиків за загрозою відмова в обслуговуванні
9. Алгоритм розрахунку та підбору технологічного обладнання
10. Алгоритм розрахунку температури поверхні чипу ІМС процесора
11. Алгоритм розрахунку теперішньої вартості ануїтету
12. Алгоритм розрахунку теперішньої вартості грошей за простими і складними відсотками

Переглядів: 2832