• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕМА 10. Системи одночасних (симулятивних) рівнянь

План

1. Поняття та приклади систем одночасних рівнянь.

2. Системи незалежних регресій.

3. Рекурсивна модель.

4. Метод непрямих найменших квадратів (НМНК).

5. Двокроковий метод найменших квадратів (2МНК).

1. Поняття та приклади систем одночасних рівнянь.В економіці часто зустрічаються задачі, які відображають багатосторонні одночасні зв‘язки між економічними явищами й описуються системою регресій.

В економетрії такі системи регресій називаються економетричними моделями.

Системи регресій, які відображають присутність одночасних багатосторонніх зв‘язків між економічними явищами, називаються системами одночасних регресій.

Наприклад:

(1),

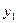- курс української гривні до курсу долара;

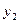– обсяг імпорту;

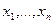– фактори, від яких залежать показники 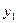та .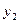

Ця модель описує економічний стан України.

Величини 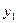та 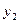, які пояснюються системою регресій, називаються ендогенними величинами.

Величини 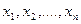, які пояснюють зміну ендогенних величин, називаються екзогенними величинами.

Як бачимо у системі (1), екзогенні величини пояснюють зміну ендогенних величин, але самі від них не залежать, тобто між даними величинами існує одностороння стохастична залежність.

2. Системи незалежних регресій.Якщо кожна з регресій має одну ендогенну величину, яка не залежить від ендогенних величин інших регресій і не здійснює на них ніякого впливу, то така економетрична модель називається системою незалежних регресій.

Найвідомішим прикладом системи незалежних регресій є регресія попиту та пропозиції, яка записуюються у такому вигляді:

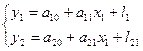(2),

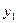-попит на окремі види товарів;

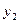-пропозиція на ці види товарів;

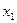-ціна на ці види товарів.

В загальному випадку система незалежних регресій має такий вигляд:

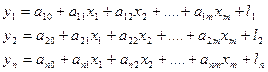(3).

Для знаходження параметрів даної системи можна застосувати МНК і записати параметри у такому вигляді:

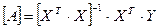(4).

3. Рекурсивна модель.Розглянемо економічну модель, яка складається з системи регресій, які, крім параметрів 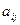при екзогенних змінних, містять параметри 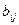при ендогенних змінних, при чому матриця параметрів 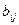має трикутну форму. Модель такого виду називається рекурсивною моделлю:

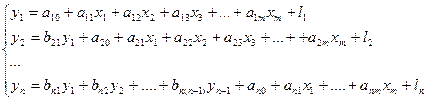Позначимо дану рекурсивну модель через (5).

Матриця [В] рекурсивної моделі має вигляд:

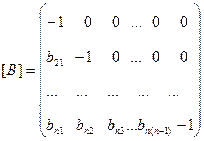(6).

Розглянемо алгоритм оцінювання параметрів рекурсивної моделі.

1. Використовуємо метод найменших квадратів для першої регресії (в правій частині першої регресії знаходяться лише змінні х) знаходимо оцінки параметрів 1-ої регресії: 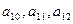і т. д.

2. Знаходимо розрахункове значення 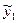з першої регресії. Будемо вважати, що значення 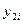наперед задане, тоді застосовуємо метод найменших квадратів до другої регресії і знаходимо параметри другої регресії і т.д.

Розглянемо приклад рекрусивної моделі Вольфанга, яка має вигляд:

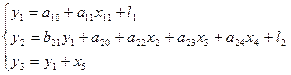(7),

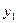- грошові доходи населення;

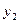- особисте споживання;

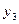- загальне споживання;

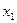- національний дохід;

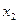- особисте споживання за попередній рік;

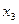- чисельність населення;

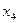- заощадження на кінець попереднього року;

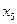- суспільний фонд споживання.

Матриця [B] даної рекурсивної моделі має вигляд:

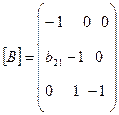(8).

Для рекурсивних моделей вводиться поняття прогнозної форми. Прогнозною формою регресивної моделі називається такий вигляд прогнозних ендогенних величин, які залежать лише від екзогенних величин:

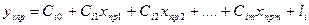(9).

Після оцінки параметрів рекурсивної моделі (5) прогнозну форму можна отримати підстановкою попередніх стохастичних залежностей ендогених змінних у наступну регресію, тобто у системі (5) перше рівняння 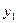підставляємо в другу регресію 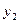і зведемо подібні доданки. До третьої регресії підставляємо 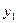та 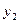вже з перетворенням і т.д.

Для визначення адекватності моделі експериментальним даним використовують критерій Фішера для кожної моделі. Розрахункове значення критерію Фішера записується у такому вигляді:

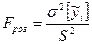, де (10);

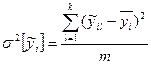(11);

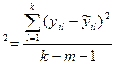S (12),

k – кількість розглянутих періодів, m – кількість оцінюваних параметрів.

4. Метод непрямих найменших квадратів (НМНК).Розглянемо систему, яка складається з двох взаємопов’язаних регресій:

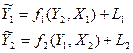(13).

Припустимо, що між ендогенними та екзогенними величинами існує лінійна залежність, тоді їх можна записати в такому вигляді:

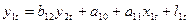(14).

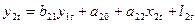
Для системи (14) розглядається питання ідентифікації.

Якщо параметри системи (14) однозначно виражаються через параметри прогнозної форми, то така економетрична модель називається ідентифікованою.

Якщо число оцінюваних параметрів системи (14) більше числа параметрів прогнозної форми, то така економетрична модель називається неідентифікованою.

Припустимо, що система ідентифікована. Розглянемо застосування непрямого методу найменших квадратів (НМНК) до даної системи.

Введемо такі позначення:

; ; ; ; .

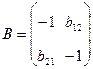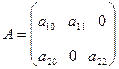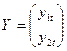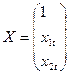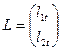В таких позначеннях систему одночасних регресій можна записати в матричній формі:

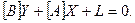(15).

Для переходу до прогнозної форми домножимо зліва рівняння в матричній формі на матрицю, обернену до матриці [B], при умові, що det [B] :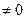

; .

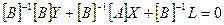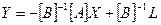Якщо позначити 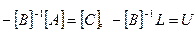, то отримаємо прогнозну форму систем регресій .

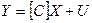Запишемо систему у розгорнутій формі:

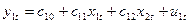
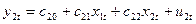(16).

Застосовуючи до кожного з рівнянь системи метод МНК, знайдемо оцінки параметрів матриці С. Використаємо позначення 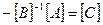. Домножимо рівняння зліва на матрицю В і отримаємо:

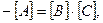або .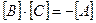

Запишемо останній вираз, використовуючи позначення у матричному вигляді:

.

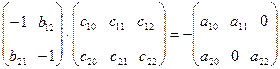Розгорнутий запис даного виразу має вигляд:

.

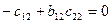
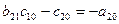
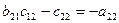Перетворимо дану систему так, щоб усі параметри 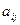та 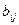виражалися через параметри :

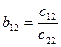
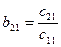
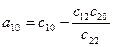(17)

.

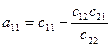
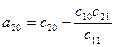
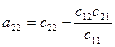Ця система задає оцінки параметрів моделі (14). Аналогічно можна застосовувати непрямий МНК і для системи з n- регресій.

5. Двокроковий метод найменших квадратів (2МНК).У тих випадках, коли система одночасних регресій неідентифікована, розроблені методи оцінювання параметрів, які враховують багатосторонні зв’язки ендогенних величин. Розглянемо систему n-взаємопов’язаних регресій у вигляді:

.................................................................................................

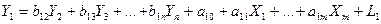
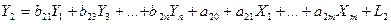
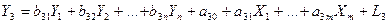
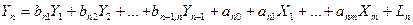
Для зручності запишемо систему у матричній формі:

. (18).

Проведемо міркування аналогічно до попереднього пункту:

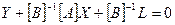, або ,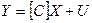

де , .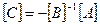

До прогнозної форми 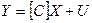застосуємо алгоритм двокрокового методу найменших квадратів (ДМНК).

1). Записується зведена форма структурних рівнянь у вигляді 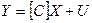, де матриця [C] записується у розгорнутому вигляді

.

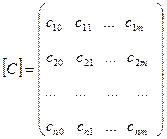Використовуючи МНК для кожної з регресій, отримаємо оцінки елементів матриці [C].

2). Використовуючи матрицю спостережень над екзогенними величинами [Х] і матрицю оцінок параметрів [C], за формулою 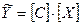знаходимо матрицю розрахункових значень ендогенних величин

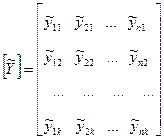, де k-кількість спостережуваних значень.

Далі повертаємося до початкової системи, записавши її у такому вигляді:

.................................................................................................

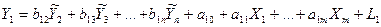
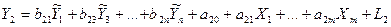
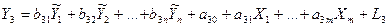
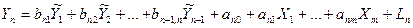
Для оцінки параметрів матриць [А] і [В] до кожного з рівнянь застосовуємо звичайний метод МНК.

Читайте також:

1. I. Органи і системи, що забезпечують функцію виділення
2. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
3. II. Анатомічний склад лімфатичної системи
4. IV. Розподіл нервової системи
5. IV. Система зв’язків всередині центральної нервової системи
6. IV. Філогенез кровоносної системи
7. POS-системи
8. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
9. VI. Філогенез нервової системи
10. А) Заробітна плата її форми та системи.
11. А) Заробітна плата, її форми та системи.
12. А) Поліпшення системи зворотного зв'язку.

Переглядів: 1412